Practical Applications - Trigonometry
Card 0 of 20
Which of the following diagrams could show a bearing of  ?
?
Which of the following diagrams could show a bearing of 
The bearing of a point B from a point A in a horizontal plane is defined as the acute angle made by the ray drawn from A through B with the north-south line through A. The bearing is read from the north or south line toward the east or west. Bearing is typically only represented in degrees (or degrees and minutes) rather than radians. To find  , start in the south direction, then move
, start in the south direction, then move  towards the west:
towards the west:

The other incorrect answer choices provided depict  ,
,  , and
, and  .
.
The bearing of a point B from a point A in a horizontal plane is defined as the acute angle made by the ray drawn from A through B with the north-south line through A. The bearing is read from the north or south line toward the east or west. Bearing is typically only represented in degrees (or degrees and minutes) rather than radians. To find 


The other incorrect answer choices provided depict 


Compare your answer with the correct one above
Which of the following could represent an aeronautical bearing of  ?
?
Which of the following could represent an aeronautical bearing of 
The correct image depicting an aeronautical bearing of  is
is

This image begins at north, and moves  clockwise from it.
clockwise from it.
Three of the given incorrect answers depict  ,
,  ,
,  . The fourth incorrect answer does not represent a standard bearing convention as it is neither an acute angle, nor in the clockwise direction. That incorrect answer looks like:
. The fourth incorrect answer does not represent a standard bearing convention as it is neither an acute angle, nor in the clockwise direction. That incorrect answer looks like:

The correct image depicting an aeronautical bearing of 

This image begins at north, and moves 
Three of the given incorrect answers depict 



Compare your answer with the correct one above
The following diagram could represent which one of these practical scenarios?

The following diagram could represent which one of these practical scenarios?

This question and its answer choices give you a few clues to work with. First, we need to identify the bearing angle being shown. The options in the answer choices are either  ,
,  , or
, or  . Because the angle begins in the south direction and moves
. Because the angle begins in the south direction and moves  towards the west, the correct bearing is
towards the west, the correct bearing is  . That means only two of the answer choices could be correct. We now need to understand how the
. That means only two of the answer choices could be correct. We now need to understand how the  miles per hour corresponds to the problem. Notice that there is no answer choice that has the bearing of
miles per hour corresponds to the problem. Notice that there is no answer choice that has the bearing of  and velocity of
and velocity of  miles per hour. Rather, we need to choose between
miles per hour. Rather, we need to choose between  miles per hour for
miles per hour for  hours or
hours or  miles per hour for
miles per hour for  hours. Because
hours. Because  miles per hour for
miles per hour for  hours corresponds to
hours corresponds to  (whereas the other option corresponds to only
(whereas the other option corresponds to only  ), the correct answer is "A motorboat traveling
), the correct answer is "A motorboat traveling  at
at  miles per hour for
miles per hour for  hours."
hours."
This question and its answer choices give you a few clues to work with. First, we need to identify the bearing angle being shown. The options in the answer choices are either 


















Compare your answer with the correct one above
A ship moves in the direction  at a speed of
at a speed of  miles per hour for
miles per hour for  hours. How far south and how far east is the ship from its starting position?
hours. How far south and how far east is the ship from its starting position?
A ship moves in the direction 


First, let's set up a diagram using the given information. This looks like this:

Next, let's convert this info into a triangle so that we can use trigonometry to solve the problem. We need to calculate that the ship going  miles per hour for
miles per hour for  hours will have traveled
hours will have traveled  miles.
miles.

Now we can use trigonometry to determine the missing sides, s and e.






Therefore the ship has travelled 181.87 miles south and 105 miles east.
First, let's set up a diagram using the given information. This looks like this:

Next, let's convert this info into a triangle so that we can use trigonometry to solve the problem. We need to calculate that the ship going 



Now we can use trigonometry to determine the missing sides, s and e.
Therefore the ship has travelled 181.87 miles south and 105 miles east.
Compare your answer with the correct one above
An airplane is traveling at a bearing of  from north for 330 kilometers. How far south and how far east is the plane from its starting point?
from north for 330 kilometers. How far south and how far east is the plane from its starting point?
An airplane is traveling at a bearing of 
First, let's incorporate the given information into a diagram. Start by labelling the plane's bearing of  along with its velocity 330km. Next, draw a line segment to complete the triangle and determine the measures of the angles of the triangle. We can determine the angle
along with its velocity 330km. Next, draw a line segment to complete the triangle and determine the measures of the angles of the triangle. We can determine the angle  , we constructed the diagram such that there is a right angle, and finally we can find the third angle by taking
, we constructed the diagram such that there is a right angle, and finally we can find the third angle by taking  .
.

The question is asking us how far south and how far east the plane is from its starting point, so we need to now use trigonometry to determine the lengths of the missing sides of the triangle. We will call these sides s for the southward distance and e for the eastward distance.


 km
km


 km
km
Therefore the airplane is 139.46 km south of its starting point and 299.08 km east of its starting point.
First, let's incorporate the given information into a diagram. Start by labelling the plane's bearing of 



The question is asking us how far south and how far east the plane is from its starting point, so we need to now use trigonometry to determine the lengths of the missing sides of the triangle. We will call these sides s for the southward distance and e for the eastward distance.


Therefore the airplane is 139.46 km south of its starting point and 299.08 km east of its starting point.
Compare your answer with the correct one above
Three ships are positioned in the following way: Ship A is 240 miles due west of Ship C, and Ship B is due south of Ship C. Ship B bears  from Ship A. How far is Ship B from Ship A? How far is Ship B from Ship C? What is the bearing from Ship A to Ship B?
from Ship A. How far is Ship B from Ship A? How far is Ship B from Ship C? What is the bearing from Ship A to Ship B?
Three ships are positioned in the following way: Ship A is 240 miles due west of Ship C, and Ship B is due south of Ship C. Ship B bears 
To solve this problem, begin with a diagram, and label all known information. We know that we can label two angles as  and one length as 240. Then, by deductive reasoning, we can label another angle as
and one length as 240. Then, by deductive reasoning, we can label another angle as  because
because  .
.

Next, we need to use trigonometry to find the answers to each question we're being asked. To find the distance AB, set up



Next, we can find the distance BC. There are two ways to do this since we know two angles of the triangle, but either way you need to use the tangent function.



Finally, we are asked to find the bearing from Ship B to A. Be careful, because in the initial problem we are given the Bearing from Ship A to Ship B. While the angle will remain the same, the direction is different because we are starting at a different initial point (B instead of A). With B as your starting point, A is north and west. Therefore the bearing from Ship B to Ship A is  .
.
Therefore the correct distance between Ships A and B is 640.67 miles, the distance between ships B and C is 594.02 miles, and the bearing from Ship B to Ship A is  .
.
To solve this problem, begin with a diagram, and label all known information. We know that we can label two angles as 



Next, we need to use trigonometry to find the answers to each question we're being asked. To find the distance AB, set up
Next, we can find the distance BC. There are two ways to do this since we know two angles of the triangle, but either way you need to use the tangent function.
Finally, we are asked to find the bearing from Ship B to A. Be careful, because in the initial problem we are given the Bearing from Ship A to Ship B. While the angle will remain the same, the direction is different because we are starting at a different initial point (B instead of A). With B as your starting point, A is north and west. Therefore the bearing from Ship B to Ship A is 
Therefore the correct distance between Ships A and B is 640.67 miles, the distance between ships B and C is 594.02 miles, and the bearing from Ship B to Ship A is 
Compare your answer with the correct one above
Three cruise ships are situated as follows: Sea Terraformer is 200 miles due north of Wave Catcher, and Island Pioneer is 345 miles due east of Wave Catcher. What is the bearing from Island Pioneer to Sea Terraformer, and what is the bearing from Sea Terraformer to Island Pioneer?
Three cruise ships are situated as follows: Sea Terraformer is 200 miles due north of Wave Catcher, and Island Pioneer is 345 miles due east of Wave Catcher. What is the bearing from Island Pioneer to Sea Terraformer, and what is the bearing from Sea Terraformer to Island Pioneer?
Begin by diagramming the given information; you'll see that the three ships create a right triangle. To solve the question, we need to find the unknown angles of the triangle, then frame our answers as the proper bearings.

First let's solve for the topmost angle in the diagram, which we'll call  .
.


By alternate interior angles, the other diagrammed angle will also be equal to  .
.
Now, put your cursor on Island Pioneer, and see if you need to move north or south, and then east or west to get to Sea Terraformer. You need to move north, then west. Therefore the bearing between Island Pioneer and Sea Terraformer is  . Now put your cursor on Sea Terraformer and complete the same process to get to Island Pioneer; you'll go south, then east. Therefore the bearing from Sea Terraformer to Island Pioneer is
. Now put your cursor on Sea Terraformer and complete the same process to get to Island Pioneer; you'll go south, then east. Therefore the bearing from Sea Terraformer to Island Pioneer is  .
.
Begin by diagramming the given information; you'll see that the three ships create a right triangle. To solve the question, we need to find the unknown angles of the triangle, then frame our answers as the proper bearings.

First let's solve for the topmost angle in the diagram, which we'll call 
By alternate interior angles, the other diagrammed angle will also be equal to 
Now, put your cursor on Island Pioneer, and see if you need to move north or south, and then east or west to get to Sea Terraformer. You need to move north, then west. Therefore the bearing between Island Pioneer and Sea Terraformer is 

Compare your answer with the correct one above
Select the answer that correctly matches the following air navigation terms to their definitions.
Select the answer that correctly matches the following air navigation terms to their definitions.
The heading of an airplane is the direction in which the airplane is pointed. The heading is measured clockwise from the north and expressed in degrees.
The airspeed is the speed of the airplane in still air.
The course of an airplane is the direction in which it moves relative to the ground. The course is measured clockwise from the north.
The groundspeed is the speed of the airplane relative to the ground.
The drift angle is the positive difference between the heading and the course.
You may use vectors to represent airspeed and heading, direction and speed of wind, or groundspeed and course. The groundspeed vector is the resultant of the airspeed vector and the wind vector.
The heading of an airplane is the direction in which the airplane is pointed. The heading is measured clockwise from the north and expressed in degrees.
The airspeed is the speed of the airplane in still air.
The course of an airplane is the direction in which it moves relative to the ground. The course is measured clockwise from the north.
The groundspeed is the speed of the airplane relative to the ground.
The drift angle is the positive difference between the heading and the course.
You may use vectors to represent airspeed and heading, direction and speed of wind, or groundspeed and course. The groundspeed vector is the resultant of the airspeed vector and the wind vector.
Compare your answer with the correct one above
In the following diagram, a blue box sits on an inclined plane. The box has weight W and exerts force  against the inclined plane and force
against the inclined plane and force  down the inclined plane. Which of the following correctly relates these vectors together?
down the inclined plane. Which of the following correctly relates these vectors together?

In the following diagram, a blue box sits on an inclined plane. The box has weight W and exerts force 


The correct answer is  because
because  and
and  are component vectors for the weight
are component vectors for the weight  .
.
The correct answer is 



Compare your answer with the correct one above
A 450 pound barrel rests on a  inclined plane. What is the minimum force (ignoring friction) needed to keep the barrel from rolling down the incline? What is the force the barrel exerts against the inclined plane? Will the barrel stay in place or roll?
inclined plane. What is the minimum force (ignoring friction) needed to keep the barrel from rolling down the incline? What is the force the barrel exerts against the inclined plane? Will the barrel stay in place or roll?
A 450 pound barrel rests on a 
First, draw a diagram of the given information. We can label the angle of inclination as  , but furthermore, in this type of problem, the angle formed between
, but furthermore, in this type of problem, the angle formed between  and
and  is equal to that same measure, so that has also been labelled
is equal to that same measure, so that has also been labelled  . Because these two angles are equal,
. Because these two angles are equal,  and
and  (see second diagram).
(see second diagram).


Using the above formulas, we get:

 lbs
lbs

 lbs
lbs
Next understand that the minimum force needed to prevent the barrel from rolling down the plane corresponds to  , so the minimum force to prevent the barrel from rolling is
, so the minimum force to prevent the barrel from rolling is  lbs. The force against the inclined plan is
lbs. The force against the inclined plan is  lbs. Finally, because
lbs. Finally, because  , the barrel will not roll down the inclined plane.
, the barrel will not roll down the inclined plane.
First, draw a diagram of the given information. We can label the angle of inclination as 







Using the above formulas, we get:


Next understand that the minimum force needed to prevent the barrel from rolling down the plane corresponds to 



Compare your answer with the correct one above
A 150 pound barrel rests on a  inclined plane. What is the minimum force (ignoring friction) needed to keep the barrel from rolling down the incline? What is the force the barrel exerts against the inclined plane? Will the barrel stay in place or roll?
inclined plane. What is the minimum force (ignoring friction) needed to keep the barrel from rolling down the incline? What is the force the barrel exerts against the inclined plane? Will the barrel stay in place or roll?
A 150 pound barrel rests on a 
We can draw a diagram of the given information, including the weight of the box and the force  against the inclined plane and the force
against the inclined plane and the force  pushing down on the inclined plane. Additionally, we can label the angle of inclination as
pushing down on the inclined plane. Additionally, we can label the angle of inclination as  , but furthermore, in this type of problem, the angle formed between
, but furthermore, in this type of problem, the angle formed between  and
and  is equal to that same measure, so that has also been labelled
is equal to that same measure, so that has also been labelled  also.
also.

Because these two angles are equal,  and
and  (see second diagram).
(see second diagram).

Using the above formulas, we get:

 lbs
lbs

 lbs
lbs
Next understand that the minimum force needed to prevent the barrel from rolling down the plane corresponds to  , so the minimum force to prevent the barrel from rolling is 31.19 lbs. The force against the inclined plan is
, so the minimum force to prevent the barrel from rolling is 31.19 lbs. The force against the inclined plan is  lbs. Finally, because
lbs. Finally, because  , the barrel will not roll down the inclined plane.
, the barrel will not roll down the inclined plane.
We can draw a diagram of the given information, including the weight of the box and the force 






Because these two angles are equal, 


Using the above formulas, we get:


Next understand that the minimum force needed to prevent the barrel from rolling down the plane corresponds to 


Compare your answer with the correct one above
A 65 pound barrel rests on a  inclined plane. What is the minimum force (ignoring friction) needed to keep the barrel from rolling down the incline? What is the force the barrel exerts against the inclined plane? Will the barrel stay in place or roll?
inclined plane. What is the minimum force (ignoring friction) needed to keep the barrel from rolling down the incline? What is the force the barrel exerts against the inclined plane? Will the barrel stay in place or roll?
A 65 pound barrel rests on a 
We can draw a diagram of the given information, including the weight of the box and the force  against the inclined plane and the force
against the inclined plane and the force  pushing down on the inclined plane. Additionally, we can label the angle of inclination as
pushing down on the inclined plane. Additionally, we can label the angle of inclination as  , but furthermore, in this type of problem, the angle formed between
, but furthermore, in this type of problem, the angle formed between  and
and  is equal to that same measure, so that has also been labelled
is equal to that same measure, so that has also been labelled  also.
also.

Because these two angles are equal,  and
and  (see second diagram).
(see second diagram).

Using the above formulas, we get:

 lbs
lbs

 lbs
lbs
Next understand that the minimum force needed to prevent the barrel from rolling down the plane corresponds to  , so the minimum force to prevent the barrel from rolling is 16.82 lbs. The force against the inclined plan is
, so the minimum force to prevent the barrel from rolling is 16.82 lbs. The force against the inclined plan is  lbs. Finally, because
lbs. Finally, because  , the barrel will not roll down the inclined plane.
, the barrel will not roll down the inclined plane.
We can draw a diagram of the given information, including the weight of the box and the force 






Because these two angles are equal, 


Using the above formulas, we get:


Next understand that the minimum force needed to prevent the barrel from rolling down the plane corresponds to 


Compare your answer with the correct one above
The heading of an airplane is  and the airspeed is
and the airspeed is  miles per hour. Find the groundspeed and course if there is a wind of
miles per hour. Find the groundspeed and course if there is a wind of  miles per hour from
miles per hour from  . Refer to the figure below.
. Refer to the figure below.

The heading of an airplane is 




To work through an air navigation problem, we must first understand how these forces act on one another. In these problems, we have three vectors: one representing airspeed, one representing wind, and one representing groundspeed. The groundspeed vector is the resultant of the airspeed and wind vectors, as you can see in the above diagram. These three vectors create a triangle.
To find the groundspeed, simply use the Pythagorean Theorem:
 miles per hour.
miles per hour.
To find the course, we need to find the smallest angle of the triangle (the angle in between the blue and purple vectors), then subtract this from the given angle of  . While we don't know that angle
. While we don't know that angle  , we can use the tangent function to find it, as below:
, we can use the tangent function to find it, as below:



We can find the course by subtraction:

Therefore the groundspeed is 222.77 miles per hour and the course is  .
.
To work through an air navigation problem, we must first understand how these forces act on one another. In these problems, we have three vectors: one representing airspeed, one representing wind, and one representing groundspeed. The groundspeed vector is the resultant of the airspeed and wind vectors, as you can see in the above diagram. These three vectors create a triangle.
To find the groundspeed, simply use the Pythagorean Theorem:

To find the course, we need to find the smallest angle of the triangle (the angle in between the blue and purple vectors), then subtract this from the given angle of 

We can find the course by subtraction:
Therefore the groundspeed is 222.77 miles per hour and the course is 
Compare your answer with the correct one above
The airspeed of an airplane is 210 kilometers per hour. There is a wind of 25 kilometers per hour from  . Find the heading and the groundspeed in order to track
. Find the heading and the groundspeed in order to track  . Refer to the figure below.
. Refer to the figure below.

The airspeed of an airplane is 210 kilometers per hour. There is a wind of 25 kilometers per hour from 


First, let's break down how this figure was constructed. In any air navigation problem, we have three vectors that create a triangle: groundspeed, airspeed, and wind. We've drawn the groundspeed vector due north, along ON. Next, the wind vector is drawn  off from the groundspeed vector, and finally, the airspeed vector closes the triangle. At this point, you can label all known quantities.
off from the groundspeed vector, and finally, the airspeed vector closes the triangle. At this point, you can label all known quantities.
To begin solving the problem, we can start by finding the groundspeed. This requires only Pythagorean Theorem to find:




Therefore the groundspeed is 208.51 kilometers per hour.
Next, let's find the heading such that the plane tracks  . Since we can't solve for the heading directly, we need to find
. Since we can't solve for the heading directly, we need to find  , then subtract it from
, then subtract it from  .
.



Now to find the heading, subtract this from  .
.
 .
.
Therefore the heading is  .
.
First, let's break down how this figure was constructed. In any air navigation problem, we have three vectors that create a triangle: groundspeed, airspeed, and wind. We've drawn the groundspeed vector due north, along ON. Next, the wind vector is drawn 
To begin solving the problem, we can start by finding the groundspeed. This requires only Pythagorean Theorem to find:
Therefore the groundspeed is 208.51 kilometers per hour.
Next, let's find the heading such that the plane tracks 


Now to find the heading, subtract this from 

Therefore the heading is 
Compare your answer with the correct one above
Determine the magnitude of vector A.

Determine the magnitude of vector A.
We can use the pythagorean theorem to solve this problem. Using  as our hypotenuse, we can drop a vertical vector perpendicular to the x-axis. We will call this
as our hypotenuse, we can drop a vertical vector perpendicular to the x-axis. We will call this  and it is 4 units in length. We can also extend a vector from the origin that connects to
and it is 4 units in length. We can also extend a vector from the origin that connects to  . We will call this
. We will call this  and it is 3 units in length.
and it is 3 units in length.
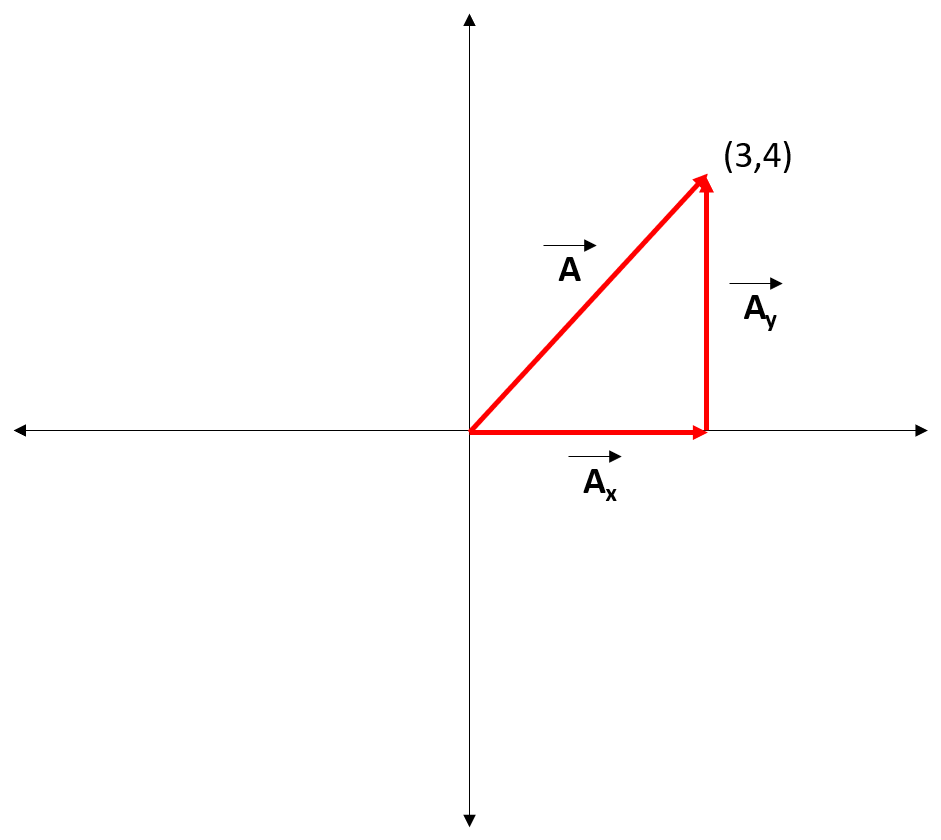
Using the pythagorean theorem:






We can use the pythagorean theorem to solve this problem. Using 



Using the pythagorean theorem:
Compare your answer with the correct one above
Which of the following is the correct term for the sum of two vectors?
Which of the following is the correct term for the sum of two vectors?
When summing two vectors, you have both an x and y component and you sum these separately leaving you with a coordinate as your answer. This coordinate is called a resultant.
When summing two vectors, you have both an x and y component and you sum these separately leaving you with a coordinate as your answer. This coordinate is called a resultant.
Compare your answer with the correct one above
Determine the resultant of  and
and  .
.
Determine the resultant of 

When determining the resultant of two vectors, you are finding the sum of two vectors. To do this you must add the x component and the y component separately.



When determining the resultant of two vectors, you are finding the sum of two vectors. To do this you must add the x component and the y component separately.
Compare your answer with the correct one above
Consider the following graphs where  begins at the origin and ends at
begins at the origin and ends at  and
and  . Which of the following depicts the correct resultant of these two vectors.
. Which of the following depicts the correct resultant of these two vectors.

Consider the following graphs where 



To find the resultant we must sum the two vectors:



Now we must graph the resultant

To find the resultant we must sum the two vectors:
Now we must graph the resultant

Compare your answer with the correct one above
How many degrees above the x-axis is  ?
?

How many degrees above the x-axis is 

First, we must understand what we are solving for. We are solving for the angle that is formed by  and the x-axis. To do this, we can extend a vector from the origin which stops directly under the end of
and the x-axis. To do this, we can extend a vector from the origin which stops directly under the end of  . We will call this new vector
. We will call this new vector  and it will be 7 units long. We will also extend a vector upwards that is perpendicular to the x-axis. We will call this
and it will be 7 units long. We will also extend a vector upwards that is perpendicular to the x-axis. We will call this  and it will be 3 units long.
and it will be 3 units long.

Now we can use the relationship that  where
where  is the adjacent side and
is the adjacent side and  is the opposite side.
is the opposite side.




And so  is 23.2 degrees above the x-axis.
is 23.2 degrees above the x-axis.
First, we must understand what we are solving for. We are solving for the angle that is formed by 




Now we can use the relationship that 


And so 
Compare your answer with the correct one above
Find the difference of the two vectors,  which ends at
which ends at  and
and  ending at
ending at  .
.
Find the difference of the two vectors, 



When finding the difference of two vectors, you must subtract the x and y components separately.



When finding the difference of two vectors, you must subtract the x and y components separately.
Compare your answer with the correct one above





















































