Phase Shifts - Trigonometry
Card 0 of 8
Which of the following is equivalent to 
Which of the following is equivalent to
The first zero can be found by plugging 3π/2 for x, and noting that it is a double period function, the zeros are every π/2, count three back and there is a zero at zero, going down.
A more succinct form for this answer is 
but that was not one of the options, so a shifted cosine must be the answer.
The first positive peak is at π/4 at -1, so the cosine function will be shifted π/4 to the right and multiplied by -1. The period and amplitude still 2, so the answer becomes 
.
To check, plug in π/4 for x and it will come out to -2.
The first zero can be found by plugging 3π/2 for x, and noting that it is a double period function, the zeros are every π/2, count three back and there is a zero at zero, going down.
A more succinct form for this answer is
The first positive peak is at π/4 at -1, so the cosine function will be shifted π/4 to the right and multiplied by -1. The period and amplitude still 2, so the answer becomes
To check, plug in π/4 for x and it will come out to -2.
Compare your answer with the correct one above
Identify the phase shift of the following equation.
Identify the phase shift of the following equation.
If we use the standard form of a sine function
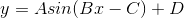
the phase shift can be calculated by 
. Therefore, in our case, our phase shift is
If we use the standard form of a sine function
the phase shift can be calculated by
Compare your answer with the correct one above
Which of the following is the correct definition of a phase shift?
Which of the following is the correct definition of a phase shift?
Take the function 
for example. The graph for 
is
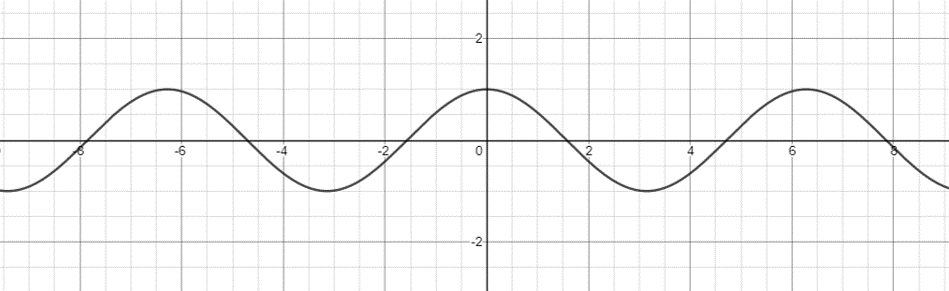
If we were to change the function to 
, our phase shift is 
. This means we need to shift our entire graph 
units to the left.
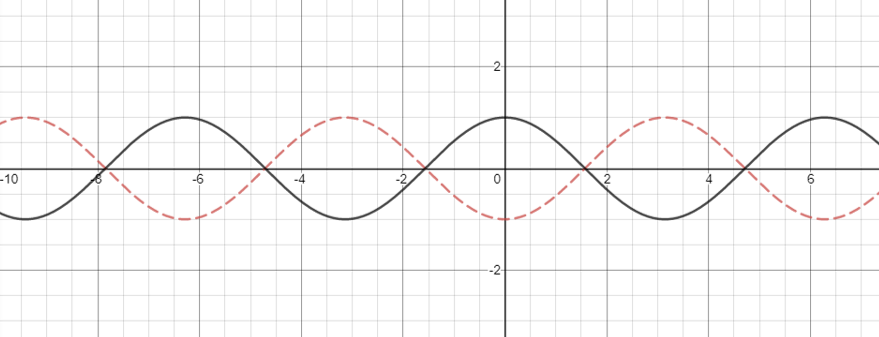
Our new graph 
is the following
Take the function 
If we were to change the function to 
Our new graph 
Compare your answer with the correct one above
Consider the function 
. What is the phase shift of this function?
Consider the function 
The general form for the secant transformation equation is 
. 
represents the phase shift of the function. When considering 
we see that 
. So our phase shift is 
and we would shift this function 
units to the left of the original secant function’s graph.
The general form for the secant transformation equation is 
Compare your answer with the correct one above
True or False: If the function 
has a phase shift of 
, then the graph will not be changed.
True or False: If the function 
This is true because the graph 
has a period of 
, meaning it repeats itself every 
units. So if 
has a phase shift of any multiple of 
, then it will just overlay the original graph. This is shown below. In orange is the graph of 
and in purple is the graph of 
.
This is true because the graph 
Compare your answer with the correct one above
Which of the following is the graph of 
with a phase shift of 
?
Which of the following is the graph of 
Start this problem by graphing the function of tangent.
Now we need to shift this graph 
to the right.
This gives us our answer
Start this problem by graphing the function of tangent.
Now we need to shift this graph 
This gives us our answer
Compare your answer with the correct one above
True or False: The function 
has a phase shift of 
.
True or False: The function 
The form of the general cosecant function is 
. So if we have 
then 
, which represents the phase shift, is equal to 
. This gives us a phase shift of 
.
The form of the general cosecant function is 
Compare your answer with the correct one above
Which of the following is the phase shift of the function 
?
Which of the following is the phase shift of the function 
The general form of the cotangent function is 
. So first we need to get 
into the form 
.
From this we see that 
giving us our answer.
The general form of the cotangent function is 
From this we see that 
Compare your answer with the correct one above