Angle Applications - Trigonometry
Card 0 of 20
What is the formula for angular velocity?
What is the formula for angular velocity?
Angular velocity is a measure of the time it takes to travel over a certain arc that is formed by a central angle.  is usually used to represent the angular velocity,
is usually used to represent the angular velocity,  is the measure of the central angle, and
is the measure of the central angle, and  is the time it takes to travel from point A to B. This formula looks similar to the measure of an arc,
is the time it takes to travel from point A to B. This formula looks similar to the measure of an arc,  , but we are considering the velocity in terms of the measure of the angle over the amount of time it took to cover that distance.
, but we are considering the velocity in terms of the measure of the angle over the amount of time it took to cover that distance.
Angular velocity is a measure of the time it takes to travel over a certain arc that is formed by a central angle. 



Compare your answer with the correct one above
True or False: The angular velocity is a measure of an angle of rotation over time.
True or False: The angular velocity is a measure of an angle of rotation over time.
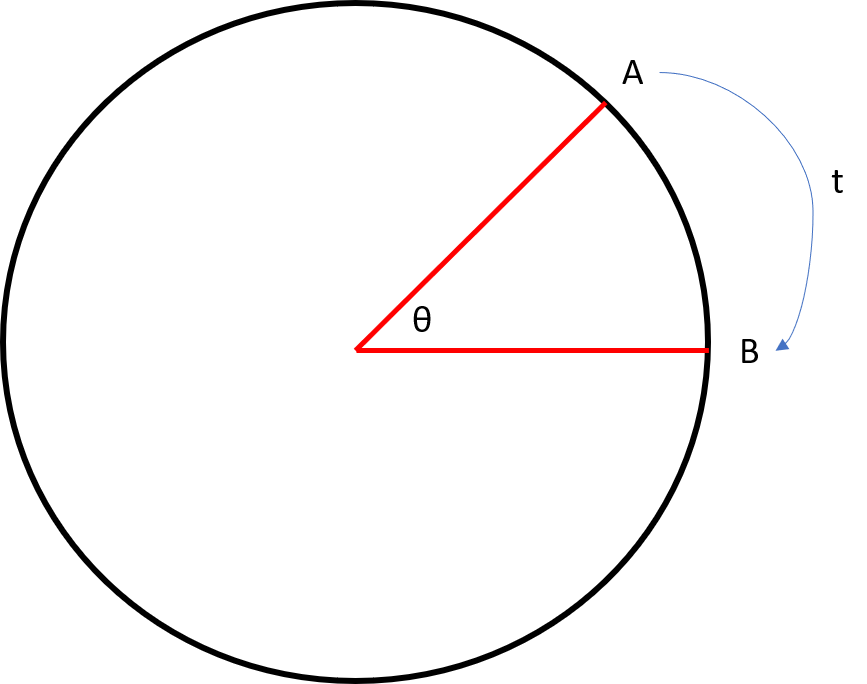
consider the figure below. Think of line A being connected to a hinge where  is. We are measuring the amount of time it takes for line A to rotate and align with line B. This is a measure of angle rotation over time.
is. We are measuring the amount of time it takes for line A to rotate and align with line B. This is a measure of angle rotation over time.

consider the figure below. Think of line A being connected to a hinge where 
Compare your answer with the correct one above
What is the angular velocity of an angle whose measure is  when it took a point 6 seconds to rotate through the angle.
when it took a point 6 seconds to rotate through the angle.
What is the angular velocity of an angle whose measure is 
We have enough information to plug into the angular velocity formula to solve this problem.  and
and  seconds.
seconds.



So our answer is  radians/seconds
radians/seconds
We have enough information to plug into the angular velocity formula to solve this problem. 

So our answer is 
Compare your answer with the correct one above
What is the angular velocity of an angle whose measure is  when it took a point 10 seconds to rotate through the angle.
when it took a point 10 seconds to rotate through the angle.
What is the angular velocity of an angle whose measure is 
We have enough information to plug into the angular velocity formula to solve this problem.  and
and  seconds.
seconds.



And so our answer is  radians/seconds.
radians/seconds.
We have enough information to plug into the angular velocity formula to solve this problem. 

And so our answer is 
Compare your answer with the correct one above
If you are walking around a circular track and your angular velocity through the angle  is
is  , how long would it take you to complete a full rotation?
, how long would it take you to complete a full rotation?
If you are walking around a circular track and your angular velocity through the angle 

This is simply solving for an unknown. Here our unknown is time,  . So we know that it takes you have an angular velocity of
. So we know that it takes you have an angular velocity of  through the angle
through the angle  . Assuming that your angular velocity is consistent, we will be able to solve for
. Assuming that your angular velocity is consistent, we will be able to solve for  . First we must manipulate our original angular velocity formula to solve for
. First we must manipulate our original angular velocity formula to solve for  .
.


Now we will plug in our known value for  and the angle of a full rotation. The angle of a full rotation is simply that of a full circle,
and the angle of a full rotation. The angle of a full rotation is simply that of a full circle,  .
.




So it takes you 24 seconds to complete a full rotation
This is simply solving for an unknown. Here our unknown is time, 




Now we will plug in our known value for 

So it takes you 24 seconds to complete a full rotation
Compare your answer with the correct one above
You are on a carousel and have completed one full rotation in 15 seconds. What is your angular velocity?
You are on a carousel and have completed one full rotation in 15 seconds. What is your angular velocity?
Even though we are not directly given an angle measurement, we are told the time it takes to complete one full rotation. One rotation is the same as the angle of an entire circle,  . Now we have enough information to plug into the angular velocity formula to solve this problem.
. Now we have enough information to plug into the angular velocity formula to solve this problem.


So the angular velocity is  radians/seconds
radians/seconds
Even though we are not directly given an angle measurement, we are told the time it takes to complete one full rotation. One rotation is the same as the angle of an entire circle, 
So the angular velocity is 
Compare your answer with the correct one above
A wheel is making one full rotation with an angular velocity of  radians/seconds. How long will it take the wheel to make 10 full rotations?
radians/seconds. How long will it take the wheel to make 10 full rotations?
A wheel is making one full rotation with an angular velocity of 
We know that the angular velocity to complete a full rotation (rotate through an angle of  ) is
) is  radians/seconds. The angle of 10 full rotations will be 10 rotations through the angle
radians/seconds. The angle of 10 full rotations will be 10 rotations through the angle  , so we multiply these two quantities.
, so we multiply these two quantities.

And this will be our  . Now we must manipulate our angular velocity formula to solve for
. Now we must manipulate our angular velocity formula to solve for  .
.


Now we can plug in our  for the 10 rotations and our angular velocity.
for the 10 rotations and our angular velocity.




And so it will take 8 seconds to make 10 rotations.
We know that the angular velocity to complete a full rotation (rotate through an angle of 


And this will be our 

Now we can plug in our 
And so it will take 8 seconds to make 10 rotations.
Compare your answer with the correct one above
If it takes you 3 seconds to rotate through an angle with an angular velocity of  , what is the measure of the angle you are rotating through?
, what is the measure of the angle you are rotating through?
If it takes you 3 seconds to rotate through an angle with an angular velocity of 
We are able to use the angular velocity formula and solve for the unknown  .
.


 (making it so we are solving for
(making it so we are solving for  )
)


We are able to use the angular velocity formula and solve for the unknown 


Compare your answer with the correct one above
Which is true of the relationship between the arc measure and the central angle as shown below?

Which is true of the relationship between the arc measure and the central angle as shown below?

Every arc has a measure that is equal to the measure of the central angle that creates the arc. This is because the measure of the angle determines the distance around the circumference that the arc makes.
Every arc has a measure that is equal to the measure of the central angle that creates the arc. This is because the measure of the angle determines the distance around the circumference that the arc makes.
Compare your answer with the correct one above
Which of the following is the correct formula for finding arc length?
Which of the following is the correct formula for finding arc length?
The circumference of an entire circle is  . When considering the length of an arc, the angle is less than
. When considering the length of an arc, the angle is less than  denoted by angle
denoted by angle  . So the formula for finding the length of an arc is replacing the angle of an entire circle,
. So the formula for finding the length of an arc is replacing the angle of an entire circle,  , with the angle that forms the arc,
, with the angle that forms the arc,  . This gives us the formula
. This gives us the formula  .
.
The circumference of an entire circle is 





Compare your answer with the correct one above
Which of the following is the correct arc length formed by the angle  of a circle whose radius is a length of 5?
of a circle whose radius is a length of 5?
Which of the following is the correct arc length formed by the angle 
We must use the formula for finding arc length  . We have been given all the information needed to just plug into the formula.
. We have been given all the information needed to just plug into the formula.



We must use the formula for finding arc length 
Compare your answer with the correct one above
Which of the following is the correct arc length formed by an angle with measure 30 degrees of a circle whose radius is a length of 3?
Which of the following is the correct arc length formed by an angle with measure 30 degrees of a circle whose radius is a length of 3?
First, we are given our angle measure in degrees and we must convert to radians to be able to use our arc length formula.

Now we are able to plug the radius length and the angle measure into our formula and solve for the arc length.



First, we are given our angle measure in degrees and we must convert to radians to be able to use our arc length formula.
Now we are able to plug the radius length and the angle measure into our formula and solve for the arc length.
Compare your answer with the correct one above
What is the measure of the angle that forms an arc with length 2.33 of a circle who has radius 4? Round to the second decimal place.
What is the measure of the angle that forms an arc with length 2.33 of a circle who has radius 4? Round to the second decimal place.
We must use the formula for finding arc length to solve for the measure of the angle,  . The formula is
. The formula is  .
.



We must use the formula for finding arc length to solve for the measure of the angle, 

Compare your answer with the correct one above
An arc has a measure of  and a diameter of 7, what is the measure of the central angle?
and a diameter of 7, what is the measure of the central angle?
An arc has a measure of 
Notice the question gave you the measure of the arc, NOT the arc length. The measure of an arc is equal to the measure of the central angle that forms the arc. We do not even need to use our formula for this one, just the fact that the central angle is equal to the measure of the arc that it forms.
Notice the question gave you the measure of the arc, NOT the arc length. The measure of an arc is equal to the measure of the central angle that forms the arc. We do not even need to use our formula for this one, just the fact that the central angle is equal to the measure of the arc that it forms.
Compare your answer with the correct one above
True or False: You are given the central angle measure but no other information, you are able to solve for the arc length.
True or False: You are given the central angle measure but no other information, you are able to solve for the arc length.
We do not have enough information to solve for the arc length. We know that the measure of the arc is equal to the central angle and that the measure of the arc is  but we still have two unknowns with no method to solve for them.
but we still have two unknowns with no method to solve for them.
We do not have enough information to solve for the arc length. We know that the measure of the arc is equal to the central angle and that the measure of the arc is 
Compare your answer with the correct one above
You know that the central angle of a sector is  and the sector area is
and the sector area is  , what is the arc length? Round to two decimals.
, what is the arc length? Round to two decimals.
You know that the central angle of a sector is 

The formula to find the area of a sector is  . The piece of information we are missing to solve for arc length is the radius, so we will use the formula for finding the area of a sector to solve for radius, allowing us to solve for the arc length.
. The piece of information we are missing to solve for arc length is the radius, so we will use the formula for finding the area of a sector to solve for radius, allowing us to solve for the arc length.






Now we can plug this into our formula to solve for arc length



The formula to find the area of a sector is 
Now we can plug this into our formula to solve for arc length
Compare your answer with the correct one above
Which of the following is the definition for a sector of a circle?
Which of the following is the definition for a sector of a circle?
Below is an illustration of a sector of a circle. A sector is the area of a circle which has been enclosed by two radii and the arc between them. A sector is not to be confused with a segment of a circle. A segment is when the area enclosed by the chord of a circle and the arc of the chord.
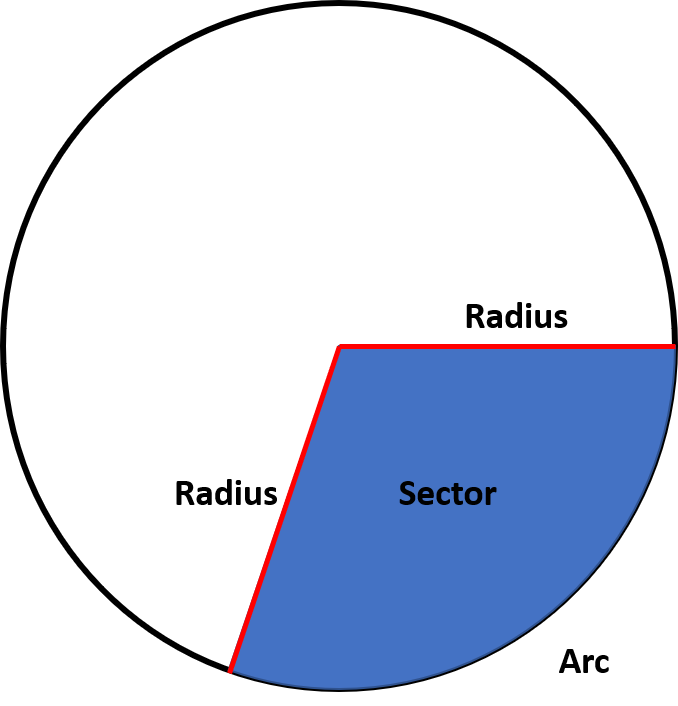
Below is an illustration of a sector of a circle. A sector is the area of a circle which has been enclosed by two radii and the arc between them. A sector is not to be confused with a segment of a circle. A segment is when the area enclosed by the chord of a circle and the arc of the chord.
Compare your answer with the correct one above
Which of the following is the formula for the area of a sector?
Which of the following is the formula for the area of a sector?
When thinking about how to derive the formula for a sector, we must consider the angle of an entire circle. The angle of an entire circle, 360 degrees, is  and we know the area of a circle is
and we know the area of a circle is  .
.
When considering a sector, this is only a portion of the entire circle, so it is a particular  out of the entire
out of the entire  . We can plug this into our area for a circle and it will simplify to the area of a sector.
. We can plug this into our area for a circle and it will simplify to the area of a sector.


When thinking about how to derive the formula for a sector, we must consider the angle of an entire circle. The angle of an entire circle, 360 degrees, is 

When considering a sector, this is only a portion of the entire circle, so it is a particular 

Compare your answer with the correct one above
If a circle has a sector with an angle of  and diameter of 4, what is the area of the sector?
and diameter of 4, what is the area of the sector?
If a circle has a sector with an angle of 
It is always best to draw a picture in order to visualize the problem you are trying to solve. The figure below shows the sector we are trying to find the area of.
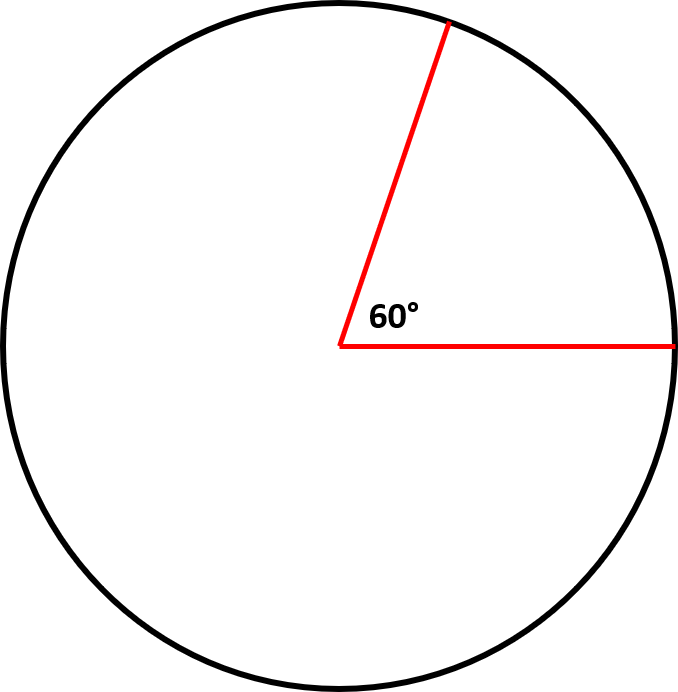
We know that the formula to find the area of a sector is  . From the information given above we know that the diameter is 4. Since we only need the radius for our formula we divide the diameter by 2 to get the radius length. The radius has a length of 2. We also know that we have our angle measure in degrees and must convert it to radians. We use the conversion formula
. From the information given above we know that the diameter is 4. Since we only need the radius for our formula we divide the diameter by 2 to get the radius length. The radius has a length of 2. We also know that we have our angle measure in degrees and must convert it to radians. We use the conversion formula  .
.

Now we can plug everything into our formula and solve.




It is always best to draw a picture in order to visualize the problem you are trying to solve. The figure below shows the sector we are trying to find the area of.
We know that the formula to find the area of a sector is 

Now we can plug everything into our formula and solve.
Compare your answer with the correct one above
True or False: The formula to find the area of a sector only works for acute angles.
True or False: The formula to find the area of a sector only works for acute angles.
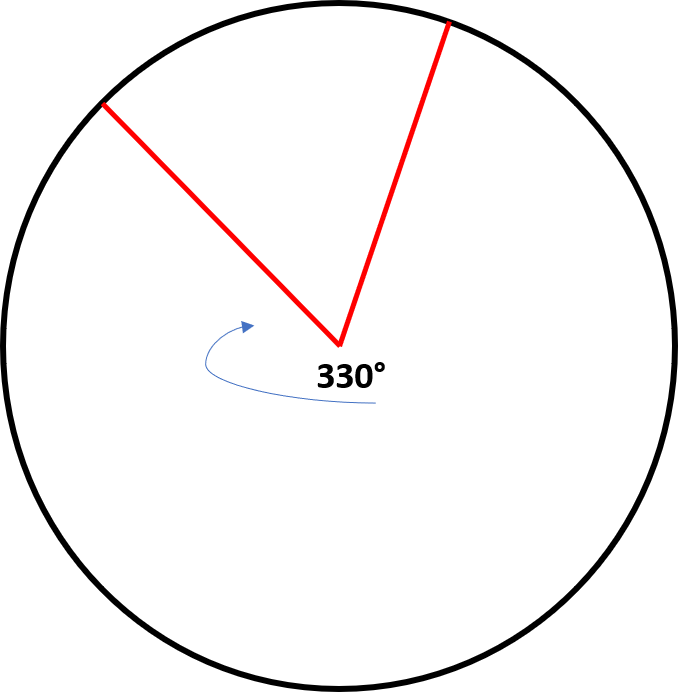
This is not true. Even obtuse angles are less than  so this formula will still work. We can demonstrate this using the sector below. The radius of the circle is 6 and the obtuse angle is 330 degrees.
so this formula will still work. We can demonstrate this using the sector below. The radius of the circle is 6 and the obtuse angle is 330 degrees.
Converting 330 degrees to radians:

We can now plug this into our formula





Now we can confirm this to be true by computing the area of the sector formed by the
area leftover formed by the acute angle, 30 degrees. To do this we will first find the total
area of the circle and then subtract the area of the sector formed by the acute angle. This should be equal to the area of the larger vector if our formula works for all angles because the sum of both sectors should be the total area of the circle.
To find the area of the circle:


To find the area of the smaller sector (note, 30 degrees in radians is  :
:




Clearly, the total area of the circle minus the area of the small sector is equal to the area
of the larger circle, therefore this formula works for all angles less than 

This is not true. Even obtuse angles are less than 
Converting 330 degrees to radians:
We can now plug this into our formula
Now we can confirm this to be true by computing the area of the sector formed by the
area leftover formed by the acute angle, 30 degrees. To do this we will first find the total
area of the circle and then subtract the area of the sector formed by the acute angle. This should be equal to the area of the larger vector if our formula works for all angles because the sum of both sectors should be the total area of the circle.
To find the area of the circle:
To find the area of the smaller sector (note, 30 degrees in radians is 
Clearly, the total area of the circle minus the area of the small sector is equal to the area
of the larger circle, therefore this formula works for all angles less than
Compare your answer with the correct one above
































































