Properties of Parallel and Perpendicular Lines - SSAT Upper Level Quantitative (Math)

Card 0 of 20

Question

Line A has equation .

Line B has equation .

Which statement is true of the two lines?

Answer

Write each statement in slope-intercept form:

Line A:

$y =-\frac{1}{7}\left ( -5x+ 20 \right )$

$y = \frac{5}{7} x-\frac{ 20}{7}$

The slope is $\frac{5}{7}$ .

Line B:

$y = -\frac{1}{5 }\left ( - 7x+ 32 \right )$

$y = \frac{7}{5}x-\frac{32}{5}$

The slope is $\frac{7}{5}$ .

The lines have differing slopes, so they are neither identical nor parallel. The product of the slopes is $\frac{5}{7} \times \frac{7}{5} = 1 e -1$ , so they are not perpendicular. The correct response is that they are distinct lines that are neither parallel nor perpendicular.

Compare your answer with the correct one above

Question

You are given three lines as follows:

Line A includes points and .

Line B includes point and has -intercept .

Line C includes the origin and point .

Which lines are parallel?

Answer

Find the slope of all three lines using the slope formula $m= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ :

Line A:

$m= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

$m= \frac{12-8}{1-3} = \frac{4}{-2} = -2$

Line B:

$m= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

$m= \frac{7-17}{6-0} = \frac{-10}{6} = -\frac{5}{3}$

Line C:

$m= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

$m= \frac{-8-0}{4-0}= \frac{-8}{4} = -2$

Lines A and C have the same slope; Line B has a different slope. Only Lines A and C are parallel.

Compare your answer with the correct one above

Question

Line P passes through the origin and point $\left ( \frac{1}{9} , \frac{1}{7}\right )$ .

Line Q passes through the origin and point $\left ( \frac{1}{9} , -\frac{1}{7}\right )$ .

Line R passes through the origin and point $\left (\frac{1}{7}, \frac{1}{9} \right )$ .

Line S passes through the origin and point $\left (\frac{1}{7}, -\frac{1}{9} \right )$ .

Which of these lines is parallel to the line of the equation ?

Answer

First, find the slope of the line of the equation by rewriting it in slope-intercept form:

$y =\frac{1}{9} \left (-7x+ 111 \right )$

$y = -\frac{7}{9}x+ \frac{111 }{9}$

The slope of this line is $-\frac{7}{9}$ , so we are looking for a line which also has this slope.

Find the slopes of all four lines by using the slope formula $m= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ . Since each line passes through the origin, this formula can be simplified to

$m= \frac{y_{2}-0}{x_{2}-0} = \frac{y_{2} }{x_{2} }$

using the other point.

Line P:

$m = \frac{y_{2} }{x_{2} }= \frac{ \frac{1}{7} }{ \frac{1}{9}} = \frac{1}{7} \div \frac{1}{9}= \frac{1}{7} \cdot \frac{9} {1} = \frac{9}{7}$

Line Q:

$m = \frac{y_{2} }{x_{2} }= \frac{- \frac{1}{7} }{ \frac{1}{9}} =- \frac{1}{7} \div \frac{1}{9}= -\frac{1}{7} \cdot \frac{9} {1} =- \frac{9}{7}$

Line R:

$m = \frac{y_{2} }{x_{2} }= \frac{ \frac{1}{9} }{ \frac{1}{7}} = \frac{1}{9} \div \frac{1}{7}= \frac{1}{9} \cdot \frac{7} {1} = \frac{7}{9}$

Line S:

$m = \frac{y_{2} }{x_{2} }= \frac{- \frac{1}{9} }{ \frac{1}{7}} = -\frac{1}{9} \div \frac{1}{7}=- \frac{1}{9} \cdot \frac{7} {1} =-\frac{7}{9}$

Line S has the desired slope and is the correct choice.

Compare your answer with the correct one above

Question

Figure NOT drawn to scale

In the above figure, . Evaluate .

Answer

The two marked angles are same-side exterior angles of two parallel lines formed by a transversal ,; by the Parallel Postulate, the angles are supplementary - the sum of their measures is 180 degrees. Therefore,

Compare your answer with the correct one above

Question

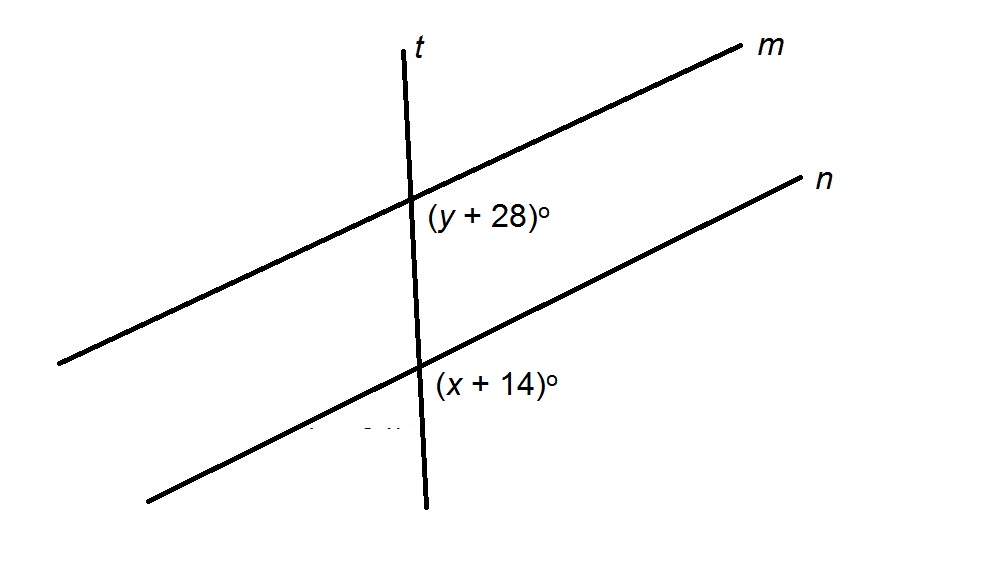
Figure NOT drawn to scale

In the above figure, . Express in terms of .

Answer

The two marked angles are corresponding angles of two parallel lines formed by a transversal, so the angles are congruent. Therefore,

Solving for by subtracting 28 from both sides:

Compare your answer with the correct one above

Question

Figure NOT drawn to scale

In the above figure, . Express in terms of .

Answer

The two marked angles are same-side interior angles of two parallel lines formed by a transversal ; by the Parallel Postulate, the angles are supplementary - the sum of their measures is 180 degrees. Therefore,

Solve for by moving the other terms to the other side and simplifying:

Compare your answer with the correct one above

Question

Figure NOT drawn to scale

In the above figure, . Evaluate .

Answer

Angles of degree measures and form a linear pair, making the angles supplementary - that is, their degree measures total 180. Therefore,

Solving for :

$4y \div 4 = 192 \div 4$

The angles of measures and form a pair of alternating interior angles of parallel lines, so, as a consequence of the Parallel Postulate, they are congruent, and

Substituting for :

Compare your answer with the correct one above

Question

Three lines are drawn on the coordinate plane.

The green line has slope $\frac{2}{3}$ , and -intercept $\frac{4}{5}$ .

The blue line has slope $\frac{3}{2}$ , and -intercept $-\frac{5}{4}$ .

The red line has slope $-\frac{2}{3}$ , and -intercept $-\frac{4}{5}$ .

Which two lines are perpendicular to each other?

Answer

To demonstrate two perpendicular lines, multiply their slopes; if their product is , then the lines are perpendicular (the -intercepts are irrelevant).

The products of these lines are given here.

Blue and green lines: $\frac{2}{3} * \frac{3}{2} = 1$

Red and green lines: $\frac{2}{3} * \left - \frac{2}{3} \right = -\frac{4}{9}$

Blue and red lines: $\frac{2}{3}* \left - \frac{3}{2} \right = -1$

It is the blue and red lines that are perpendicular.

We can also see that their slopes are negative reciprocals, indicating perpendicular lines.

Compare your answer with the correct one above

Question

Two perpendicular lines intersect at point . One line also includes point . What is the slope of the other line?

Answer

The slopes of two perpendicular lines are the opposites of each other's reciprocals.

To find the slope of the first line substitute $x_{1} = 3, y_{1} =8, x_{2} = 4, y_{2} =-1$ in the slope formula:

$m =\frac{ y_{1}-y_{2}}{ x_{1}-x_{2}}$

$m =\frac{ 8 - (-1)}{ 3-4} = \frac{ 9}{ -1} = -9$

The slope of the first line is , so the slope of the second line is the opposite reciprocal of this, which is $\frac{1}{9}$ .

Compare your answer with the correct one above

Question

Two perpendicular lines intersect at the origin; one line also passes through point . What is the slope of the other line?

Answer

The slopes of two perpendicular lines are the opposites of each other's reciprocals.

To find the slope of the first line, substitute $x_{1} = 5, y_{1} =7, x_{2} = 0, y_{2} =0$ in the slope formula:

$m =\frac{ y_{1}-y_{2}}{ x_{1}-x_{2}}$

$m =\frac{ 7-0}{5-0}=\frac{ 7}{5}$

The slope of the first line is $\frac{ 7}{5}$ , so the slope of the second line is the opposite reciprocal of this, which is $-\frac{5}{ 7}$ .

Compare your answer with the correct one above

Question

Which of the following lines is perpendicular to the line ?

Answer

All we care about for this problem is the slopes of the lines...the x- and y-intercepts are irrelevant.

Remember that the slopes of perpendicular lines are opposite reciprocals. By putting the given equation into form, we can see that its slope is $\frac{3}{5}$ . So we are looking for a line with a slope of $-\frac{5}{3}$ .

The equation can be put into the form $y=-\frac{5}{3}x+6$ , and so we know that it is perpendicular to the given line.

Compare your answer with the correct one above

Question

Line A passes through the origin and .

Line B passes through the origin and $\left ( -36, 64\right )$ .

Line C passes through the origin and $\left ( \frac{1}{12},- \frac{1}{16} \right )$ .

Line D passes through the origin and .

Line E passes through the origin and $\left ( \sqrt{2},-\sqrt{3} \right )$ .

Which line is perpendicular to Line A?

Answer

Find the slopes of all five lines using the slope formula $m= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ . Since each line passes through the origin, this formula can be simplified to

$m= \frac{y_{2}-0}{x_{2}-0} = \frac{y_{2} }{x_{2} }$

using the other point.

Line A:

$m = \frac{6 }{8 } = \frac{3}{4}$

The correct line must have as its slope the opposite of the reciprocal of this, which is $m = -\frac{4}{3}$ .

Line B:

$m = \frac{64 }{-36}= - \frac{16}{9}$

Line C:

$m = \frac{ -\frac{1}{16} }{ \frac{1}{12}} = -\frac{1}{16} \div \frac{1}{12} = -\frac{1}{16} \cdot \frac{12} {1}= -\frac{12}{16} = -\frac{3}{4}$

Line D:

$m = \frac{-1.2 }{0.9 } = -\frac{12}{9} = -\frac{4}{3}$

Line E:

$m = \frac{ - \sqrt{3}}{ \sqrt{2} } = -\frac{\sqrt{6}}{2}$

Of the last four lines, only Line D has the desired slope.

Compare your answer with the correct one above

Question

Line W passes through the origin and point $\left (\frac{1}{4}, \frac{1}{9} \right )$ .

Line X passes through the origin and point $\left (\frac{1}{4}, -\frac{1}{9} \right )$ .

Line Y passes through the origin and point $\left ( \frac{1}{9} , \frac{1}{4}\right )$ .

Line Z passes through the origin and point $\left ( \frac{1}{9} , -\frac{1}{4}\right )$ .

Which of these lines is perpendicular to the line of the equation ?

Answer

First, find the slope of the line of the equation by rewriting it in slope-intercept form:

$y =-\frac{1}{9} \left (-4x+100 \right )$

$y = \frac{4}{9} x-\frac{100 }{9}$

The slope of this line is $\frac{4}{9}$ , so we are looking for a line whose slope is the opposite of the reciprocal of this, or $-\frac{9}{4}$ .

Find the slopes of all four lines by using the slope formula $m= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ . Since each line passes through the origin, this formula can be simplified to

$m= \frac{y_{2}-0}{x_{2}-0} = \frac{y_{2} }{x_{2} }$

using the other point.

Line W:

$m = \frac{y_{2} }{x_{2} }= \frac{ \frac{1}{9} }{ \frac{1}{4}} = \frac{1}{9} \div \frac{1}{4}= \frac{1}{9} \cdot \frac{4} {1} = \frac{4}{9}$

Line X:

$m = \frac{y_{2} }{x_{2} }= \frac{ - \frac{1}{9} }{ \frac{1}{4}} =- \frac{1}{9} \div \frac{1}{4}= -\frac{1}{9} \cdot \frac{4} {1} =- \frac{4}{9}$

Line Y:

$m = \frac{y_{2} }{x_{2} }= \frac{ \frac{1}{4} }{ \frac{1}{9}} = \frac{1}{4} \div \frac{1}{9}= \frac{1}{4} \cdot \frac{9} {1} = \frac{9}{4}$

Line Z:

$m = \frac{y_{2} }{x_{2} }= \frac{ -\frac{1}{4} }{ \frac{1}{9}} =-\frac{1}{4} \div \frac{1}{9}= -\frac{1}{4} \cdot \frac{9} {1} = -\frac{9}{4}$

Line Z has the desired slope and is the correct choice.

Compare your answer with the correct one above

Question

Determine whether the two equations are parallel, perpendicular or neither, and choose the best reason.

$-2x+6y = 3 \textup{ and } -\frac{y}{3}=1$

Answer

Convert both equations to slope intercept form:

$y=\frac{1}{3}x+\frac{1}{2}$

The slope of the first equation is $m_1=\frac{1}{3}$ .

Convert the second equation.

$-\frac{y}{3}=1$

The slope of this equation is zero since there is no term!

In order for the two functions to be parallel, they must have the same slopes.

In order for the two functions to be perpendicular, their slopes must be the negative reciprocal to each other.

Since there's no correlation with both slopes, the equations are neither parallel or perpendicular to each other.

The correct answer is:

Neither, the slopes have no correlation

Compare your answer with the correct one above

Question

Given: the following three lines on the coordinate plane:

Line 1: The line of the equation

Line 2: The line of the equation

Line 3: The line of the equation

Which of the following is a true statement?

Answer

Line 1, the line of the equation , is a vertical line on the coordinate plane; Line 2, the line of the equation , is a horizontal line. Lines 1 and 2 are perpendicular to each other.

The slope of Line 3, the line of the equation , can be calculated by putting the equation in slope-intercept form:

The slope is , which makes it perpendicular to a line of slope $-\frac{1}{-1} = 1$ . Line 1, being vertical, has undefined slope, and Line 2, being horizontal, has slope 0.

Correct response: Line 1 and Line 2 are perpendicular; Line 3 is perpendicular to neither.

Compare your answer with the correct one above

Question

Given: the following three lines on the coordinate plane:

Line 1: The line of the equation

Line 2: The line of the equation

Line 3: The line of the equation

Which of the following is a true statement?

Answer

The slope of each line can be calculated by putting the equation in slope-intercept form and noting the coefficient of :

Line 1:

$\frac{2y }{2}= \frac{-1x + 12}{2}$

$y= -\frac{1}{2}x+6$

Slope of Line 1: $-\frac{1}{2}$

Line 2:

Slope of Line 2:

Line 3: The equation is already in slope-intercept form; its slope is 2.

Two lines are perpendicular if and only their slopes have product . The slopes of Lines 1 and 3 have product $-\frac{1}{2} \cdot 2 = -1$ ; they are perpendicular. The slopes of Lines 1 and 2 have product $-\frac{1}{2} \cdot (- 2 )= 1$ ; they are not perpendicular. The slopes of Lines 2 and 3 have product $-2 \cdot 2 = -4$ ; they are not perpendicular.

Correct response: Line 1 and Line 3 are perpendicular; Line 2 is perpendicular to neither.

Compare your answer with the correct one above

Question

The line of the equation is perpendicular to which of the following lines on the coordinate plane?

Answer

First, find the slope of the line by rewriting the equation in slope-intercept form and noting the coefficient of :

$\frac{- 8y}{-8} =\frac{ -6x+17}{-8}$

$y = \frac{3}{4}x-\frac{17}{8}$

The line has slope $\frac{3}{4}$ .

A line perpendicular to this would have slope $-1 \div \frac{3}{4} = -\frac{4}{3}$ . Of the four equations among the choices, all of which are in slope-intercept form, only $y =- \frac{4}{3}x$ has this slope.

Compare your answer with the correct one above

Question

One side of a rectangle on the coordinate plane has as its endpoints the points and .

What would be the slope of a side adjacent to this side?

Answer

First, we find the slope of the segment connecting or . Using the formula

$m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

and setting

$x_{1} = 2, y_{1}=4, x_{2}= 9, y_{2} = -1$

we get

$m = \frac{-1-4}{9-2}= \frac{-5}{7} = -\frac{5}{7}$

Adjacent sides of a rectangle are perpendicuar, so their slopes will be the opposites of each other's reciprocals. Therefore, the slope of an adjacent side will be the opposite of the reciprocal of $-\frac{5}{7}$ , which is $\frac{7}{5}$ .

Compare your answer with the correct one above

Question

Lines 1 and 2, which are perpendicular, have their -intercepts at the point . The -intercept of Line 1 is at the point . Give the -intercept of Line 2.

Answer

The slope of a line with -intercept and -intercept is $m = -\frac {b}{a}$ . For Line 1, , so Line 1 has slope $-\frac{8}{5}$ . The slope of Line 2, which is perpendicular to Line 1, will be the opposite of the reciprocal of this, which is $\frac{5}{8}$ . Setting equal to this and , we get

$\frac{5}{8}= -\frac {8}{a}$ , or $\frac{5}{8}= \frac {-8}{a}$

Cross-multiplying:

$\frac{5a }{5}= \frac{-64}{5}$

$a = -12 \frac{4}{5}$

The -intercept of Line 2 is $\left ( -12 \frac{4}{5}, 0 \right )$ .

Compare your answer with the correct one above

Question

Which of the following choices gives the equations of a pair of perpendicular lines with the same -intercept?

Answer

All of the equations are given in slope-intercept form , so we can answer this question by examining the coefficients of , which are the slopes, and the constants, which are the -intercepts. In each case, since the lines are perpendicular, each -coefficient must be the other's opposite reciprocal, and since the lines have the same -intercept, the constants must be equal.

Of the five pairs, only

and $y = - \frac{1}{4}x + \frac{1}{8}$

and

$y = \frac{2}{5}x + 9$ and $y = - \frac{5}{2}x + 9$

have equations whose -coefficients are the other's opposite reciprocal. Of these, only the latter pair of equations have equal constant terms.

$y = \frac{2}{5}x + 9$ and $y = - \frac{5}{2}x + 9$

is the correct choice.

Compare your answer with the correct one above

Tap the card to reveal the answer