Lines - SSAT Middle Level Math
Card 0 of 13
Figure NOT drawn to scale.
Evaluate 
.
Figure NOT drawn to scale.
Evaluate
By the Segment Addition Postulate,
By the Segment Addition Postulate,
Compare your answer with the correct one above
Figure NOT drawn to scale.
Evaluate 
.
Figure NOT drawn to scale.
Evaluate
By the Segment Addition Postulate,
By the Segment Addition Postulate,
Compare your answer with the correct one above
What is the length of a line segment with end points 
and 
?
What is the length of a line segment with end points
The length of a line segment can be determined using the distance formula:
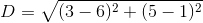
The length of a line segment can be determined using the distance formula:
Compare your answer with the correct one above
What is the length of a line with endpoints 
and 
.
What is the length of a line with endpoints
To find the length of this line, you can subtract 
to get 
. Since the y-coordinates are the same, you don't have to take any vertical direction into account. Therefore, you only look at the x-coordinates!
To find the length of this line, you can subtract
Compare your answer with the correct one above
Find the length of the line segment whose endpoints are 
and 
.
Find the length of the line segment whose endpoints are
We can use the distance formula:
We can use the distance formula:
Compare your answer with the correct one above
The point 
lies on a circle. What is the length of the radius of the circle if the center is located at 
?
The point
The radius is the distance from the center of the circle to anypoint on the circle. So we can use the distance formula in order to find the radius of the circle:
The radius is the distance from the center of the circle to anypoint on the circle. So we can use the distance formula in order to find the radius of the circle:
Compare your answer with the correct one above
The coordinates of 
and 
are 
and 
. Find the length of the diagonal of the following rectangle:
The coordinates of
A rectangle has two diagonals with the same length. So we should find the length of 
. We can use the distance formula:
A rectangle has two diagonals with the same length. So we should find the length of
Compare your answer with the correct one above
The radius of a circle is 6 inches. What is one-third of the diameter?
The radius of a circle is 6 inches. What is one-third of the diameter?
If the radius is equal to 6 inches, then the diameter will be double that value, or 12 inches. One-third of 12 is 4, which is therefore the correct answer.
If the radius is equal to 6 inches, then the diameter will be double that value, or 12 inches. One-third of 12 is 4, which is therefore the correct answer.
Compare your answer with the correct one above
If a circle has a radius of 12 inches, the biggest line that would be drawn within the circle is:
If a circle has a radius of 12 inches, the biggest line that would be drawn within the circle is:
The largest line that can be drawn within a circle is the diamater. The diameter is equal to twice the radius. Given that the radius is equal to 12 inches, the largest line that could be drawn (the diameter) would be equal to 24 inches.
The largest line that can be drawn within a circle is the diamater. The diameter is equal to twice the radius. Given that the radius is equal to 12 inches, the largest line that could be drawn (the diameter) would be equal to 24 inches.
Compare your answer with the correct one above
A right triangle has one leg with a length of 6 feet and a hypotenuse of 10 feet. What is the length of the other leg?
A right triangle has one leg with a length of 6 feet and a hypotenuse of 10 feet. What is the length of the other leg?
In geometry, a right angle triangle can occur with the ratio of 
in which 3 and 4 are each leg lengths, and 5 is the hypotenuse.
When you know the length of two sides of a right angle triangle like this, you can calculate the third side using this ratio.
Here, the ratio is:
This is double the 
ratio. Therefore, we should multiply 4 by 2 in order to solve for the missing leg, which would be a value of 8 feet.
Another way to solve is to use the Pythagorean Theorem: 
.
We know that one leg is 6 feet and the hypotenuse is 10 feet.
In geometry, a right angle triangle can occur with the ratio of
When you know the length of two sides of a right angle triangle like this, you can calculate the third side using this ratio.
Here, the ratio is:
This is double the
Another way to solve is to use the Pythagorean Theorem:
We know that one leg is 6 feet and the hypotenuse is 10 feet.
Compare your answer with the correct one above
The diameter of a circle is 
centimeters. What is one-fourth of the circle's radius?
The diameter of a circle is
By definition, the radius 
and diameter 
of a circle are related by the following equation:
Plugging in 
as stated in the question, we find that 
.
Since the question is asking us for the value of 
:
.
By definition, the radius
Plugging in
Since the question is asking us for the value of
Compare your answer with the correct one above
A right triangle has one leg with length 
and another leg with length 
. What is the length of the hypotenuse?
A right triangle has one leg with length
Since we are dealing with a right triangle, we can use the Pythagorean Theorem:
,
where 
and 
are leg lengths of 
and 
, respectively, and 
is the length of the hypotenuse.
Substituting values into the Theorem:
Since we are dealing with a right triangle, we can use the Pythagorean Theorem:
where
Substituting values into the Theorem:
Compare your answer with the correct one above
Line 
has a length of 
. It is bisected at point 
, and the resulting segment 
is bisected again at point 
. What is the length of the line segment 
?
Line
A line that is bisected is split into two segments of equal length. Therefore, if line 
is bisected at point 
,
.
Consequently, bisecting line segment 
at point 
:
A line that is bisected is split into two segments of equal length. Therefore, if line
Consequently, bisecting line segment
Compare your answer with the correct one above