How to find the area of a triangle - SSAT Middle Level Math

Card 0 of 20

Question

What is the area of a triangle with a base of and a height of ?

Answer

The formula for the area of a triangle is $\dpi{100} Area=\frac{1}{2}\times base\times height$ .

Plug the given values into the formula to solve:

$\dpi{100} Area=\frac{1}{2}\times 12\times 3$

$\dpi{100} Area=\frac{1}{2}\times 36$

$\dpi{100} Area=18$

Compare your answer with the correct one above

Question

A right triangle has legs 90 centimeters and 16 centimeters, What is its area?

Answer

The legs of a right triangle are its base and height, so use the area formula for a triangle with these dimension. Setting :

$A = \frac{1}{2} bh = \frac{1}{2} \cdot 16 \cdot 90= 720$

Compare your answer with the correct one above

Question

A triangle has base 18 inches and height 14 inches. What is its area?

Answer

Use the area formula for a triangle, setting :

$A = \frac{1}{2} bh = \frac{1}{2} \cdot 18 \cdot14 = 126$

Compare your answer with the correct one above

Question

What is the area of the above triangle?

Answer

The two legs of a right triangle can serve as its base and its height. The area of the triangle is half the product of the two:

$\frac{1}{2} \cdot 7 \cdot 24 = 84$

That is, the area is 84 square inches.

Compare your answer with the correct one above

Question

What is the area of the above triangle?

Answer

The two legs of a right triangle can serve as its base and its height. The area of the triangle is half the product of the two:

$\frac{1}{2} \cdot 50 \cdot 120 = 3,000$

That is, the area is 3,000 square millimeters.

Compare your answer with the correct one above

Question

Note: Figure NOT drawn to scale.

The above triangle has an area of 450 square centimers. $x = 20 \textrm{ cm}$ . What is ?

Answer

The area of a triangle is one half the product of its base and its height - in the above diagram, that means

$A = \frac{1}{2}xy$ .

Substitute , and solve for :

$\frac{1}{2} \cdot 20 \cdot y = 450$

$10 \cdot y = 450$

$10 \cdot y \div 10 = 450 \div 10$

$y = 45 \textrm{ cm}$

Compare your answer with the correct one above

Question

Please use the following shape for the question.

What is the area of this shape?

Answer

From this shape we are able to see that we have a square and a triangle, so lets split it into the two shapes to solve the problem. We know we have a square based on the 90 degree angles placed in the four corners of our quadrilateral.

Since we know the first part of our shape is a square, to find the area of the square we just need to take the length and multiply it by the width. Squares have equilateral sides so we just take 5 times 5, which gives us 25 inches squared.

We now know the area of the square portion of our shape. Next we need to find the area of our right triangle. Since we know that the shape below the triangle is square, we are able to know the base of the triangle as being 5 inches, because that base is a part of the square's side.

To find the area of the triangle we must take the base, which in this case is 5 inches, and multipy it by the height, then divide by 2. The height is 3 inches, so 5 times 3 is 15. Then, 15 divided by 2 is 7.5.

We now know both the area of the square and the triangle portions of our shape. The square is 25 inches squared and the triangle is 7.5 inches squared. All that is remaining is to added the areas to find the total area. Doing this gives us 32.5 inches squared.

Compare your answer with the correct one above

Question

Find the area of the triangle.

Note: Figure not drawn to scale.

Answer

To find the area of a triangle, multiply the base of the triangle by the height and then divide by two.

Compare your answer with the correct one above

Question

The hypotenuse of a right triangle is 25 inches; it has one leg 15 inches long. Give its area in square feet.

Answer

The area of a right triangle is half the product of the lengths of its legs, so we need to use the Pythagorean Theorem to find the length of the other leg. Set :

$a^{2} = c^{2} - b^{2}$

$a^{2} = 25^{2} - 15^{2}$

$a^{2} = 625-225$

$a^{2} =400$

$a = \sqrt{400} = 20$

The legs are 15 and 20 inches long. Divide both dimensions by 12 to convert from inches to feet:

$20 \div 12 = \frac{5}{3}$ feet

$15 \div 12 = \frac{5}{4}$ feet

Now find half their product:

$A = \frac{1}{2} \times \frac{5}{3}\times \frac{5}{4} = \frac{25}{24} = 1 \frac{1}{24}$ square feet

Compare your answer with the correct one above

Question

The hypotenuse of a right triangle is feet; it has one leg feet long. Give its area in square inches.

Answer

The area of a right triangle is half the product of the lengths of its legs, so we need to use the Pythagorean Theorem to find the length of the other leg. Set :

$a^{2} = c^{2} - b^{2}$

$a^{2} = 39 ^{2} - 36^{2}$

$a^{2} = 1,521 - 1,296$

$a^{2} = 225$

$a = \sqrt{225} = 15$

The legs have length and feet; multiply both dimensions by to convert to inches:

$15 \times 12 = 180$ inches

$36 \times 12 = 432$ inches.

Now find half the product:

$A = \frac{1}{2} \cdot 180 \cdot 432 = 38,880\ in^{2}$

Compare your answer with the correct one above

Question

What is the area of the triangle?

Answer

Area of a triangle can be determined using the equation:

$\small A=\frac{1}{2}bh$

$\small A=\frac{1}{2}(14)(5)=35$

Compare your answer with the correct one above

Question

A triangle has a height of 9 inches and a base that is one third as long as the height. What is the area of the triangle, in square inches?

Answer

The area of a triangle is found by multiplying the base times the height, divided by 2.

$\text{Area} =\frac{\text{base}\times \text{height}}{2}$

Given that the height is 9 inches, and the base is one third of the height, the base will be 3 inches.

$b=h\div3=9\div3=3$

We now have both the base (3) and height (9) of the triangle. We can use the equation to solve for the area.

$\text{Area} =\frac{9\times 3}{2}$

$\text{Area} =\frac{27}{2}$

The fraction cannot be simplified.

Compare your answer with the correct one above

Question

What is the area (in square feet) of a triangle with a base of feet and a height of feet?

Answer

The area of a triangle is found by multiplying the base times the height, divided by .

$Area =\frac{base\cdot height}{2}$

$Area =\frac{4\cdot 7}{2}$

Compare your answer with the correct one above

Question

Note: Figure NOT drawn to scale.

What percent of the above figure is green?

Answer

The area of the entire rectangle is the product of its length and width, or

$120 \times 50 = 6,000$ .

The area of the right triangle is half the product of its legs, or

$\frac{1}{2} \times 40 \times 80 = 1,600$

The area of the green region is therefore the difference of the two, or

.

The green region is therefore

$\frac{4,400}{6,000} \times 100 = 73 \frac{1}{3} %$

of the rectangle.

Compare your answer with the correct one above

Question

Note: Figure NOT drawn to scale.

Refer to the above diagram. Give the ratio of the area of the green region to that of the white region.

Answer

The area of the entire rectangle is the product of its length and width, or

$120 \times 50 = 6,000$ .

The area of the right triangle is half the product of its legs, or

$\frac{1}{2} \times 40 \times 80 = 1,600$

The area of the green region is therefore the difference of the two, or

.

The ratio of the area of the green region to that of the white region is

$\frac{4,400}{1,600} = \frac{4,400 \div 400}{1,600\div 400} = \frac{11}{4}$

That is, 11 to 4.

Compare your answer with the correct one above

Question

The quadrilateral in the above diagram is a square. What percent of it is white?

Answer

The area of the entire square is the square of the length of a side, or

$80 \times 80 = 6,400$ .

The area of the white right triangle is half the product of its legs, or

$\frac{1}{2} \times 30 \times 60 = 900$ .

Therefore, the area of that triangle is

$\frac{900 }{6,400} \times 100 = 14 \frac{1}{16} %$

of that of the entire square.

Compare your answer with the correct one above

Question

Mr. Jones owns the isosceles-triangle-shaped parcel of land seen in the above diagram. He sells the parcel represented in red to his brother. What is the area of the land he retains?

Answer

The area of a triangle is half the product of its base and its height, so Mr. Jones's parcel originally had area

$\frac{1}{2} \times 140 \times 160 = 11,200$ square meters.

The portion he sold his brother, represented by the red right triangle, has area

$\frac{1}{2} \times 56 \times 128 = 3,584$ square meters.

Therefore, the area of the parcel Mr. Jones retained is

square meters.

Compare your answer with the correct one above

Question

Find the area of the triangle below

Answer

The equation for area of a triangle is

$\frac{b\times h}{2}$ .

In this case the coordinates of the base are , which means the length of the base is .

The coordinates of the side that determines the height are .

Therefore the height is .

$\frac{8\times8}{2}=\frac{64}{2}=32$ .

Compare your answer with the correct one above

Question

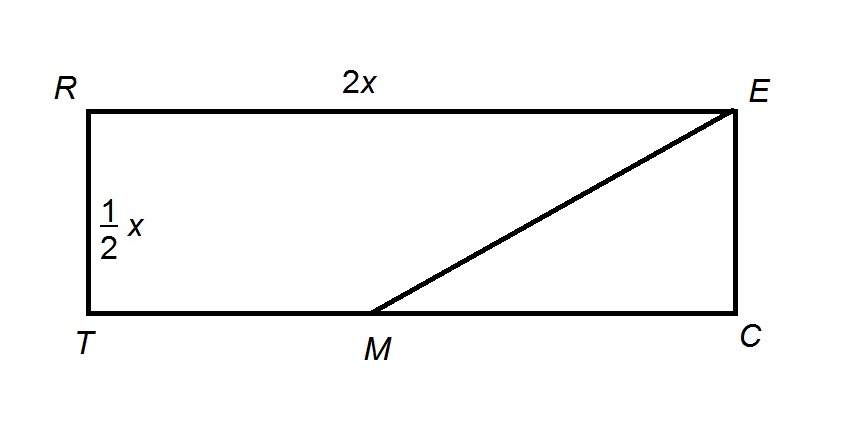
The above diagram shows Rectangle , with midpoint of $\overline{CT}$ .

The area of $\bigtriangleup ECM$ is 225. Evaluate

Answer

is the midpoint of $\overline{CT}$ , so $\bigtriangleup ECM$ has as its base $CM= \frac{1}{2} \cdot CT = \frac{1}{2} \cdot 2x =x$ ; its height is $EC = \frac{1}{2} x$ .

Its area is half their product, or

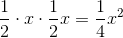
$\frac{1}{2} \cdot x \cdot \frac{1}{2} x = \frac{1}{4} x^{2}$

Set this equal to 225:

$\frac{1}{4} x^{2} = 225$

$4 \cdot \frac{1}{4} x^{2} = 4 \cdot 225$

$x^{2} = 900$

$x = \sqrt{900}= 30$ .

Compare your answer with the correct one above

Question

Give the perimeter of the above triangle in feet.

Answer

The perimeter of the triangle - the sum of the lengths of its sides - is

inches.

Divide by 12 to convert to feet:

$30 \div 12 = 2 \textrm{ R }6$

As a fraction, this is $2 \frac{6}{12}$ or $2 \frac{1}{2}$ feet,

Compare your answer with the correct one above

Tap the card to reveal the answer