Inequalities & Absolute Value - SAT Math
Card 0 of 20
If 
and 
, which of the following must be true?
If 
Systems of inequalities can be solved just like systems of equations, but with three important caveats:
-
You can only use the Elimination Method, not the Substitution Method. Since you only solve for ranges in inequalities (e.g. a < 5) and not for exact numbers (e.g. a = 5), you can't make a direct number-for-variable substitution.
-
In order to combine inequalities, the inequality signs must be pointed in the same direction.
-
When you're combining inequalities, you should always add, and never subtract. Since subtraction of inequalities is akin to multiplying by -1 and adding, this causes errors with flipped signs and negated terms. Always look to add inequalities when you attempt to combine them.
With all of that in mind, here you can stack these two inequalities and add them together:
Notice that the 
terms cancel, and that with 
on top and 
on bottom you're left with only one variable, 
. The new inequality hands you the answer, 
.
Note that if this were to appear on the calculator-allowed section, you could just graph the inequalities and look for their overlap to use process of elimination on the answer choices. These two inequalities intersect at the point (15, 39).
Systems of inequalities can be solved just like systems of equations, but with three important caveats:
-
You can only use the Elimination Method, not the Substitution Method. Since you only solve for ranges in inequalities (e.g. a < 5) and not for exact numbers (e.g. a = 5), you can't make a direct number-for-variable substitution.
-
In order to combine inequalities, the inequality signs must be pointed in the same direction.
-
When you're combining inequalities, you should always add, and never subtract. Since subtraction of inequalities is akin to multiplying by -1 and adding, this causes errors with flipped signs and negated terms. Always look to add inequalities when you attempt to combine them.
With all of that in mind, here you can stack these two inequalities and add them together:
Notice that the 
Note that if this were to appear on the calculator-allowed section, you could just graph the inequalities and look for their overlap to use process of elimination on the answer choices. These two inequalities intersect at the point (15, 39).
Compare your answer with the correct one above
Based on the system of inequalities above, which of the following must be true?
Based on the system of inequalities above, which of the following must be true?
Systems of inequalities can be solved just like systems of equations, but with three important caveats:
-
You can only use the Elimination Method, not the Substitution Method. Since you only solve for ranges in inequalities (e.g. a < 5) and not for exact numbers (e.g. a = 5), you can't make a direct number-for-variable substitution.
-
In order to combine inequalities, the inequality signs must be pointed in the same direction.
-
When you're combining inequalities, you should always add, and never subtract. Since subtraction of inequalities is akin to multiplying by -1 and adding, this causes errors with flipped signs and negated terms. Always look to add inequalities when you attempt to combine them.
With all of that in mind, you can add these two inequalities together to get:
So 
. This matches an answer choice, so you're done. Note that process of elimination is hard here, given that 
is always a positive variable on the "greater than" side of the inequality, meaning it can be as large as you want it to be. And as long as 
is larger than 
, 
can be extremely large or extremely small. This is why systems of inequalities problems are best solved through algebra; the possibilities can be endless trying to visualize numbers, but the algebra will help you find the direct, known limits.
Systems of inequalities can be solved just like systems of equations, but with three important caveats:
-
You can only use the Elimination Method, not the Substitution Method. Since you only solve for ranges in inequalities (e.g. a < 5) and not for exact numbers (e.g. a = 5), you can't make a direct number-for-variable substitution.
-
In order to combine inequalities, the inequality signs must be pointed in the same direction.
-
When you're combining inequalities, you should always add, and never subtract. Since subtraction of inequalities is akin to multiplying by -1 and adding, this causes errors with flipped signs and negated terms. Always look to add inequalities when you attempt to combine them.
With all of that in mind, you can add these two inequalities together to get:
So 
Compare your answer with the correct one above
If x > r and y < s, which of the following must also be true?
If x > r and y < s, which of the following must also be true?
Because of all the variables here, many students are tempted to pick their own numbers to try to prove or disprove each answer choice. But an important technique for dealing with systems of inequalities involves treating them almost exactly like you would systems of equations, just with three important caveats:
-
You can only use the Elimination Method, not the Substitution Method. Since you only solve for ranges in inequalities (e.g. a < 5) and not for exact numbers (e.g. a = 5), you can't make a direct number-for-variable substitution.
-
In order to combine inequalities, the inequality signs must be pointed in the same direction.
-
When you're combining inequalities, you should always add, and never subtract. Since subtraction of inequalities is akin to multiplying by -1 and adding, this causes errors with flipped signs and negated terms. Always look to add inequalities when you attempt to combine them.
Here, the first step is to get the signs pointing in the same direction. You already have x > r, so flip the other inequality to get s > y (which is the same thing − you’re not actually manipulating it; if y is less than s, then of course s is greater than y). Now you have:
x > r
s > y
And you can add the inequalities:
x + s > r + y
That’s similar to but not exactly like an answer choice, so now look at the other answer choices. Two of them involve the x and y term on one side and the s and r term on the other, so you can then subtract the same variables (y and s) from each side to arrive at:
x - y > r - s
Because of all the variables here, many students are tempted to pick their own numbers to try to prove or disprove each answer choice. But an important technique for dealing with systems of inequalities involves treating them almost exactly like you would systems of equations, just with three important caveats:
-
You can only use the Elimination Method, not the Substitution Method. Since you only solve for ranges in inequalities (e.g. a < 5) and not for exact numbers (e.g. a = 5), you can't make a direct number-for-variable substitution.
-
In order to combine inequalities, the inequality signs must be pointed in the same direction.
-
When you're combining inequalities, you should always add, and never subtract. Since subtraction of inequalities is akin to multiplying by -1 and adding, this causes errors with flipped signs and negated terms. Always look to add inequalities when you attempt to combine them.
Here, the first step is to get the signs pointing in the same direction. You already have x > r, so flip the other inequality to get s > y (which is the same thing − you’re not actually manipulating it; if y is less than s, then of course s is greater than y). Now you have:
x > r
s > y
And you can add the inequalities:
x + s > r + y
That’s similar to but not exactly like an answer choice, so now look at the other answer choices. Two of them involve the x and y term on one side and the s and r term on the other, so you can then subtract the same variables (y and s) from each side to arrive at:
x - y > r - s
Compare your answer with the correct one above
If 
and 
, which of the following must be true?
If 
Systems of inequalities can be solved just like systems of equations, but with three important caveats:
-
You can only use the Elimination Method, not the Substitution Method. Since you only solve for ranges in inequalities (e.g. a < 5) and not for exact numbers (e.g. a = 5), you can't make a direct number-for-variable substitution.
-
In order to combine inequalities, the inequality signs must be pointed in the same direction.
-
When you're combining inequalities, you should always add, and never subtract. Since subtraction of inequalities is akin to multiplying by -1 and adding, this causes errors with flipped signs and negated terms. Always look to add inequalities when you attempt to combine them.
So what does that mean for you here? You have two inequalities, one dealing with 
and one dealing with 
. But all of your answer choices are one equality with both 
and 
in the comparison. Since your given inequalities are both "greater than," meaning the signs are pointing in the same direction, you can add those two inequalities together:
Sums to:
And now you can just divide both sides by 3, and you have:
Which matches an answer choice and is therefore your correct answer.
Systems of inequalities can be solved just like systems of equations, but with three important caveats:
-
You can only use the Elimination Method, not the Substitution Method. Since you only solve for ranges in inequalities (e.g. a < 5) and not for exact numbers (e.g. a = 5), you can't make a direct number-for-variable substitution.
-
In order to combine inequalities, the inequality signs must be pointed in the same direction.
-
When you're combining inequalities, you should always add, and never subtract. Since subtraction of inequalities is akin to multiplying by -1 and adding, this causes errors with flipped signs and negated terms. Always look to add inequalities when you attempt to combine them.
So what does that mean for you here? You have two inequalities, one dealing with 
Sums to:
And now you can just divide both sides by 3, and you have:
Which matches an answer choice and is therefore your correct answer.
Compare your answer with the correct one above
Which of the following consists of the 
-coordinates of all the points that satisfy the system of inequalities above?
Which of the following consists of the 
Systems of inequalities can be solved just like systems of equations, but with three important caveats:
-
You can only use the Elimination Method, not the Substitution Method. Since you only solve for ranges in inequalities (e.g. a < 5) and not for exact numbers (e.g. a = 5), you can't make a direct number-for-variable substitution.
-
In order to combine inequalities, the inequality signs must be pointed in the same direction.
-
When you're combining inequalities, you should always add, and never subtract. Since subtraction of inequalities is akin to multiplying by -1 and adding, this causes errors with flipped signs and negated terms. Always look to add inequalities when you attempt to combine them.
Here you have the signs pointing in the same direction, but you don't have the same coefficients for 
in order to eliminate it to be left with only 
terms (which is your goal, since you're being asked to solve for a range for 
). So you will want to multiply the second inequality by 3 so that the coefficients match. That yields:
When you then stack the two inequalities and sum them, you have:
Yields:
You can then divide both sides by 4 to get your answer:
Systems of inequalities can be solved just like systems of equations, but with three important caveats:
-
You can only use the Elimination Method, not the Substitution Method. Since you only solve for ranges in inequalities (e.g. a < 5) and not for exact numbers (e.g. a = 5), you can't make a direct number-for-variable substitution.
-
In order to combine inequalities, the inequality signs must be pointed in the same direction.
-
When you're combining inequalities, you should always add, and never subtract. Since subtraction of inequalities is akin to multiplying by -1 and adding, this causes errors with flipped signs and negated terms. Always look to add inequalities when you attempt to combine them.
Here you have the signs pointing in the same direction, but you don't have the same coefficients for 
When you then stack the two inequalities and sum them, you have:
Yields:
You can then divide both sides by 4 to get your answer:
Compare your answer with the correct one above
Which of the following consists of the 
-coordinates of all of the points that satisfy the system of inequalities above?
Which of the following consists of the 
This systems of inequalities problem rewards you for creative algebra that allows for the transitive property. You know that 
, and since you're being asked about 
you want to get as much value out of that statement as you can. And while you don't know exactly what 
is, the second inequality does tell you about 
. Note that algebra allows you to add (or subtract) the same thing to both sides of an inequality, so if you want to learn more about 
, you can just add 
to both sides of that second inequality. In doing so, you'll find that 
becomes 
, or 
.
Now you have two inequalities that each involve 
. If 
and 
, then by the transitive property, 
.
This systems of inequalities problem rewards you for creative algebra that allows for the transitive property. You know that 
Now you have two inequalities that each involve 
Compare your answer with the correct one above
Which of the following represents the complete set of values for 
that satisfy the system of inequalities above?
Which of the following represents the complete set of values for 
Systems of inequalities can be solved just like systems of equations, but with three important caveats:
-
You can only use the Elimination Method, not the Substitution Method. Since you only solve for ranges in inequalities (e.g. a < 5) and not for exact numbers (e.g. a = 5), you can't make a direct number-for-variable substitution.
-
In order to combine inequalities, the inequality signs must be pointed in the same direction.
-
When you're combining inequalities, you should always add, and never subtract. Since subtraction of inequalities is akin to multiplying by -1 and adding, this causes errors with flipped signs and negated terms. Always look to add inequalities when you attempt to combine them.
Here you should see that the 
terms have the same coefficient (2), meaning that if you can move them to the same side of their respective inequalities, you'll be able to combine the inequalities and eliminate the 
variable. To do so, subtract 
from both sides of the second inequality, making the system:
(the first, unchanged inequality)
(the new second inequality)
When you sum these inequalities, you're left with:
Here is where you need to remember an important rule about inequalities: if you multiply or divide by a negative, you must flip the sign. So to divide by -2 to isolate 
, you will have to flip the sign:
Systems of inequalities can be solved just like systems of equations, but with three important caveats:
-
You can only use the Elimination Method, not the Substitution Method. Since you only solve for ranges in inequalities (e.g. a < 5) and not for exact numbers (e.g. a = 5), you can't make a direct number-for-variable substitution.
-
In order to combine inequalities, the inequality signs must be pointed in the same direction.
-
When you're combining inequalities, you should always add, and never subtract. Since subtraction of inequalities is akin to multiplying by -1 and adding, this causes errors with flipped signs and negated terms. Always look to add inequalities when you attempt to combine them.
Here you should see that the 
When you sum these inequalities, you're left with:
Here is where you need to remember an important rule about inequalities: if you multiply or divide by a negative, you must flip the sign. So to divide by -2 to isolate 
Compare your answer with the correct one above
If 
and 
, which of the following must be true?
If 
When students face abstract inequality problems, they often pick numbers to test outcomes. But that can be time-consuming and confusing - notice that with so many variables and each given inequality including subtraction, you'd have to consider the possibilities of positive and negative numbers for each, numbers that are close together vs. far apart. There are lots of options.
The more direct way to solve features performing algebra. Notice that with two steps of algebra, you can get both inequalities in the same terms, of 
. If you add 
to both sides of 
you get:
And if you add 
to both sides of 
you get:
If you then combine the inequalities you know that 
and 
, so it must be true that 
.
When students face abstract inequality problems, they often pick numbers to test outcomes. But that can be time-consuming and confusing - notice that with so many variables and each given inequality including subtraction, you'd have to consider the possibilities of positive and negative numbers for each, numbers that are close together vs. far apart. There are lots of options.
The more direct way to solve features performing algebra. Notice that with two steps of algebra, you can get both inequalities in the same terms, of 
And if you add 
If you then combine the inequalities you know that 
Compare your answer with the correct one above
Which of the following is a possible value of x given the system of inequalities below?
3x+4y > 54
-4x+2y < 10
Which of the following is a possible value of x given the system of inequalities below?
3x+4y > 54
-4x+2y < 10
In order to combine this system of inequalities, we’ll want to get our signs pointing the same direction, so that we’re able to add the inequalities. We’re also trying to solve for the range of x in the inequality, so we’ll want to be able to eliminate our other unknown, y. In order to accomplish both of these tasks in one step, we can multiply both signs of the second inequality by -2, giving us
3x+4y > 54 (our original first inequality)
8x-4y > -10 (our new, manipulated second inequality)
We can now add the inequalities, since our signs are the same direction (and when I start with something larger and add something larger to it, the end result will universally be larger) to arrive at
3x+4y > 54
+8x-4y > -10
11x > 44
Thus, dividing by 11 gets us to
x > 4. Only positive 5 complies with this simplified inequality.
In order to combine this system of inequalities, we’ll want to get our signs pointing the same direction, so that we’re able to add the inequalities. We’re also trying to solve for the range of x in the inequality, so we’ll want to be able to eliminate our other unknown, y. In order to accomplish both of these tasks in one step, we can multiply both signs of the second inequality by -2, giving us
3x+4y > 54 (our original first inequality)
8x-4y > -10 (our new, manipulated second inequality)
We can now add the inequalities, since our signs are the same direction (and when I start with something larger and add something larger to it, the end result will universally be larger) to arrive at
3x+4y > 54
+8x-4y > -10
11x > 44
Thus, dividing by 11 gets us to
x > 4. Only positive 5 complies with this simplified inequality.
Compare your answer with the correct one above
Which of the following set of coordinates is within the graphed solution set for the system of inequalities below?
x+2y > 16
-3x+y < 1
Which of the following set of coordinates is within the graphed solution set for the system of inequalities below?
x+2y > 16
-3x+y < 1
In order to combine this system of inequalities, we’ll want to get our signs pointing the same direction, so that we’re able to add the inequalities. We’ll also want to be able to eliminate one of our variables. In order to do so, we can multiply both sides of our second equation by -2, arriving at
x+2y > 16 (our original first inequality)
6x- 2y > -2 (our new, manipulated second inequality)
Adding these inequalities gets us to
x+2y > 16
+6x- 2y > -2
7x > 14
Dividing this inequality by 7 gets us to
x > 2.
Thus, the only possible value for x in the given coordinates is 3, in the coordinate set (3, 8), our correct answer.
Note - if you encounter an example like this one in the calculator-friendly section, you can graph the system of inequalities and see which set applies. The graph will, in this case, look like:
And we can see that the point (3, 8) falls into the overlap of both inequalities. We could also test both inequalities to see if the results comply with the set of numbers, but would likely need to invest more time in such an approach. Here, drawing conclusions on the basis of x is likely the easiest no-calculator way to go!
In order to combine this system of inequalities, we’ll want to get our signs pointing the same direction, so that we’re able to add the inequalities. We’ll also want to be able to eliminate one of our variables. In order to do so, we can multiply both sides of our second equation by -2, arriving at
x+2y > 16 (our original first inequality)
6x- 2y > -2 (our new, manipulated second inequality)
Adding these inequalities gets us to
x+2y > 16
+6x- 2y > -2
7x > 14
Dividing this inequality by 7 gets us to
x > 2.
Thus, the only possible value for x in the given coordinates is 3, in the coordinate set (3, 8), our correct answer.
Note - if you encounter an example like this one in the calculator-friendly section, you can graph the system of inequalities and see which set applies. The graph will, in this case, look like:
And we can see that the point (3, 8) falls into the overlap of both inequalities. We could also test both inequalities to see if the results comply with the set of numbers, but would likely need to invest more time in such an approach. Here, drawing conclusions on the basis of x is likely the easiest no-calculator way to go!
Compare your answer with the correct one above
Which of the following, if solved, would yield the set of all real numbers that are exactly 15 units away from -3?
Which of the following, if solved, would yield the set of all real numbers that are exactly 15 units away from -3?
If you're looking for a number exactly 
units to either side of 
, you need an absolute value equation that gives you answers of 
and 
.
One way forward is to simply solve each equation for 
using the two-case method, assuming first that the expression within the absolute value signs positive and then that it is negative and solving the resulting equation for each case.
If you do so, choice 
becomes: 
, or 
and 
, or 
, which is correct.
Choice 
becomes: 
, or 
, which doesn't work.
Choice 
becomes: 
, or 
, which doesn't match.
Choice 
becomes: 
, or 
, which doesn't work.
You could also quickly solve this question if you remember the general way number line absolute value problems like this one work. Each one will be in the general form 
, where the "Distance" referenced is the distance from the center value to one of the two values for 
.
So in this case the "center value" would be 
and the "distance" would be 
, yielding an equation of 
.
If you're looking for a number exactly 
One way forward is to simply solve each equation for 
If you do so, choice 
Choice 
Choice 
Choice 
You could also quickly solve this question if you remember the general way number line absolute value problems like this one work. Each one will be in the general form 
So in this case the "center value" would be 
Compare your answer with the correct one above
If 
is an integer, what is the value of 
such that 
is minimized?
If 
Any time you have an absolute value equation and a question that is asking for the smallest possible value for the expression, remember that absolute value expressions can be zero but can never be less than 0. There are two ways to solve a problem like the one given. The first is by finding the value of 
such that the expression within the absolute value signs is zero and then finding the closest integer to that number. The second is by inspection (simply using brute force to find the value for xx that will minimize the value given).
If you set 
, and that 
. Since 
, the closest integer value is 
, which will yield a value of 
.
The other way to approach this problem is by inspection, or through brute force. Try plugging in a few values for 
to see what happens.
If 
then the expression is 
If 
, then the expression is 
.
If x=2x=2 then the expression becomes 
.
Notice that the function decreases and then increases around 
, indicating that (for integer values, at least) 
will yield the smallest result for 
.
Any time you have an absolute value equation and a question that is asking for the smallest possible value for the expression, remember that absolute value expressions can be zero but can never be less than 0. There are two ways to solve a problem like the one given. The first is by finding the value of 
If you set 
The other way to approach this problem is by inspection, or through brute force. Try plugging in a few values for 
If 
If 
If x=2x=2 then the expression becomes 
Notice that the function decreases and then increases around 
Compare your answer with the correct one above
Which of the following equations describes the set of all real numbers that are 
units away from 
?
Which of the following equations describes the set of all real numbers that are 
This problem is a perfect candidate to test the answer choices, as the calculations required are not particularly difficult but the algebraic setup can be quite challenging to conceptualize. If you look for the two numbers that are 66 units away from −4−4, they are:
Then plug those values in as 
and see which equations work. For answer choice 
, 
does equal 
, and 
also equals 
, so 
satisfies the equation.
This problem is a perfect candidate to test the answer choices, as the calculations required are not particularly difficult but the algebraic setup can be quite challenging to conceptualize. If you look for the two numbers that are 66 units away from −4−4, they are:
Then plug those values in as 
Compare your answer with the correct one above
Which of the following equations describes the set of all real numbers that are 2 units away from -3?
Which of the following equations describes the set of all real numbers that are 2 units away from -3?
Even if you're unsure of where to start on this problem, you should have a head start. The problem is testing absolute values, and you should know that the result of any absolute value is always nonnegative, 
. So the answer choices that include an absolute value equalling a negative number must be incorrect: that just cannot be possible.
To test the remaining choices, consider that the numbers that are exactly two units away from -3 are -3+2 = -1, and -3-2 = -5. When you plug these numbers in for 
in the answer choices, only one is valid:
gives you:
--> 
--> 
Therefore this absolute value satisfies the given situation, and is correct.
Even if you're unsure of where to start on this problem, you should have a head start. The problem is testing absolute values, and you should know that the result of any absolute value is always nonnegative, 
To test the remaining choices, consider that the numbers that are exactly two units away from -3 are -3+2 = -1, and -3-2 = -5. When you plug these numbers in for 
Therefore this absolute value satisfies the given situation, and is correct.
Compare your answer with the correct one above
For what value of 
is 
?
For what value of 
It is important to recognize that absolute values must be nonnegative, 
. That means that for this given expression, the 
can only go as low as 
, and then the second part of the expression asks you to add 
. So this expression can never equal zero: it's an absolute value added to 1, so the lowest this expression can be is 1.
It is important to recognize that absolute values must be nonnegative, 
Compare your answer with the correct one above
Which of the following choices provides the complete solution set for the equation 
?
Which of the following choices provides the complete solution set for the equation 
To solve an absolute value like this, recognize that there are two outcomes inside an absolute value that would have it equal 3. If the inside of an absolute value expression is 3, then the result is 3. Or if the inside of an absolute value expression equals -3, the absolute value will equal 3. So you can solve this as two equations:
and 
.
Solving for the first one, you have:
And solving for the second one, you have:
Therefore, the correct answer is:
To solve an absolute value like this, recognize that there are two outcomes inside an absolute value that would have it equal 3. If the inside of an absolute value expression is 3, then the result is 3. Or if the inside of an absolute value expression equals -3, the absolute value will equal 3. So you can solve this as two equations:
Solving for the first one, you have:
And solving for the second one, you have:
Therefore, the correct answer is:
Compare your answer with the correct one above
What is the sum of the two solutions to the equation 
?
What is the sum of the two solutions to the equation 
To solve an equation with an absolute value, recognize that there are two things that would make an absolute value equal 5: the inside of the absolute value could equal 5, or it could equal -5. So your job is to solve for both possibilities:
Possibility 1:
You can then subtract 3 from both sides to get:
And divide both sides by 2 to finish:
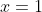
Possibility 2:
Subtract 3 from both sides to get:
Divide both sides by 2:
Your two solutions are 1 and -4. Since the question wants the sum of the two answers, you can add them together to get your answer, -3.
To solve an equation with an absolute value, recognize that there are two things that would make an absolute value equal 5: the inside of the absolute value could equal 5, or it could equal -5. So your job is to solve for both possibilities:
Possibility 1:
You can then subtract 3 from both sides to get:
And divide both sides by 2 to finish:
Possibility 2:
Subtract 3 from both sides to get:
Divide both sides by 2:
Your two solutions are 1 and -4. Since the question wants the sum of the two answers, you can add them together to get your answer, -3.
Compare your answer with the correct one above
What is the sum of all real-number solutions to the equation 
?
What is the sum of all real-number solutions to the equation 
When you're solving equations involving absolute values, it's important to recognize that there are generally two solutions. Here if the inside of the absolute value equals 1, you've solved for 
-- or if the inside of the absolute value equals -1 you've also solved for 
. So you should solve this as two equations:
Possibility 1
Here you can add 7 to both sides to get:
And then divide both sides by 2:
Possibility 2
Add 7 to both sides:
And divide both sides by 2:
The question asks for the sum of all answers, so add 
to get the right answer, 
When you're solving equations involving absolute values, it's important to recognize that there are generally two solutions. Here if the inside of the absolute value equals 1, you've solved for 
Possibility 1
Here you can add 7 to both sides to get:
And then divide both sides by 2:
Possibility 2
Add 7 to both sides:
And divide both sides by 2:
The question asks for the sum of all answers, so add 
Compare your answer with the correct one above
For which value of 
is the equation 
true?
For which value of 
An important thing to know about absolute values is that their minimum value is zero; absolute values must be nonnegative. So here if you take the result of an absolute value and then add 1 to it, it simply cannot equal 0. To do so, the absolute value itself would have to equal -1, and that is just not possible.
An important thing to know about absolute values is that their minimum value is zero; absolute values must be nonnegative. So here if you take the result of an absolute value and then add 1 to it, it simply cannot equal 0. To do so, the absolute value itself would have to equal -1, and that is just not possible.
Compare your answer with the correct one above
Which of the following equations describes the set of all real numbers that are 5 units away from -3?
Which of the following equations describes the set of all real numbers that are 5 units away from -3?
One helpful shortcut on this problem is just understanding that the result of an absolute value can never be negative. So an answer choice like 
simply cannot be correct: it's not a valid equation.
Of course, there are three remaining choices so your guessing probability isn't high enough to quit now. To solve this, first think about which values are 5 units away from -3. Since -3 + 5 = 2, and -3 - 5 = -8, you have two values that you know fit the definition: 2 and -8.
Now plug those numbers into the answer choices to see which fit with one of the absolute values. You'll see that 
fits:
, so this satisfies 
, so this satisfies 
One helpful shortcut on this problem is just understanding that the result of an absolute value can never be negative. So an answer choice like 
Of course, there are three remaining choices so your guessing probability isn't high enough to quit now. To solve this, first think about which values are 5 units away from -3. Since -3 + 5 = 2, and -3 - 5 = -8, you have two values that you know fit the definition: 2 and -8.
Now plug those numbers into the answer choices to see which fit with one of the absolute values. You'll see that 
Compare your answer with the correct one above