Acute / Obtuse Triangles - SAT Math
Card 0 of 20
If the average of the measures of two angles in a triangle is 75o, what is the measure of the third angle in this triangle?
If the average of the measures of two angles in a triangle is 75o, what is the measure of the third angle in this triangle?
The sum of the angles in a triangle is 180o: a + b + c = 180
In this case, the average of a and b is 75:
(a + b)/2 = 75, then multiply both sides by 2
(a + b) = 150, then substitute into first equation
150 + c = 180
c = 30
The sum of the angles in a triangle is 180o: a + b + c = 180
In this case, the average of a and b is 75:
(a + b)/2 = 75, then multiply both sides by 2
(a + b) = 150, then substitute into first equation
150 + c = 180
c = 30
Compare your answer with the correct one above
Which of the following can NOT be the angles of a triangle?
Which of the following can NOT be the angles of a triangle?
In a triangle, there can only be one obtuse angle. Additionally, all the angle measures must add up to 180.
In a triangle, there can only be one obtuse angle. Additionally, all the angle measures must add up to 180.
Compare your answer with the correct one above
Let the measures, in degrees, of the three angles of a triangle be x, y, and z. If y = 2z, and z = 0.5x - 30, then what is the measure, in degrees, of the largest angle in the triangle?
Let the measures, in degrees, of the three angles of a triangle be x, y, and z. If y = 2z, and z = 0.5x - 30, then what is the measure, in degrees, of the largest angle in the triangle?
The measures of the three angles are x, y, and z. Because the sum of the measures of the angles in any triangle must be 180 degrees, we know that x + y + z = 180. We can use this equation, along with the other two equations given, to form this system of equations:
x + y + z = 180
y = 2z
z = 0.5x - 30
If we can solve for both y and x in terms of z, then we can substitute these values into the first equation and create an equation with only one variable.
Because we are told already that y = 2z, we alreay have the value of y in terms of z.
We must solve the equation z = 0.5x - 30 for x in terms of z.
Add thirty to both sides.
z + 30 = 0.5x
Mutliply both sides by 2
2(z + 30) = 2z + 60 = x
x = 2z + 60
Now we have the values of x and y in terms of z. Let's substitute these values for x and y into the equation x + y + z = 180.
(2z + 60) + 2z + z = 180
5z + 60 = 180
5z = 120
z = 24
Because y = 2z, we know that y = 2(24) = 48. We also determined earlier that x = 2z + 60, so x = 2(24) + 60 = 108.
Thus, the measures of the three angles of the triangle are 24, 48, and 108. The question asks for the largest of these measures, which is 108.
The answer is 108.
The measures of the three angles are x, y, and z. Because the sum of the measures of the angles in any triangle must be 180 degrees, we know that x + y + z = 180. We can use this equation, along with the other two equations given, to form this system of equations:
x + y + z = 180
y = 2z
z = 0.5x - 30
If we can solve for both y and x in terms of z, then we can substitute these values into the first equation and create an equation with only one variable.
Because we are told already that y = 2z, we alreay have the value of y in terms of z.
We must solve the equation z = 0.5x - 30 for x in terms of z.
Add thirty to both sides.
z + 30 = 0.5x
Mutliply both sides by 2
2(z + 30) = 2z + 60 = x
x = 2z + 60
Now we have the values of x and y in terms of z. Let's substitute these values for x and y into the equation x + y + z = 180.
(2z + 60) + 2z + z = 180
5z + 60 = 180
5z = 120
z = 24
Because y = 2z, we know that y = 2(24) = 48. We also determined earlier that x = 2z + 60, so x = 2(24) + 60 = 108.
Thus, the measures of the three angles of the triangle are 24, 48, and 108. The question asks for the largest of these measures, which is 108.
The answer is 108.
Compare your answer with the correct one above
Angles x, y, and z make up the interior angles of a scalene triangle. Angle x is three times the size of y and 1/2 the size of z. How big is angle y.
Angles x, y, and z make up the interior angles of a scalene triangle. Angle x is three times the size of y and 1/2 the size of z. How big is angle y.
The answer is 18
We know that the sum of all the angles is 180. Using the rest of the information given we can write the other two equations:
x + y + z = 180
x = 3y
2x = z
We can solve for y and z in the second and third equations and then plug into the first to solve.
x + (1/3)x + 2x = 180
3\[x + (1/3)x + 2x = 180\]
3x + x + 6x = 540
10x = 540
x = 54
y = 18
z = 108
The answer is 18
We know that the sum of all the angles is 180. Using the rest of the information given we can write the other two equations:
x + y + z = 180
x = 3y
2x = z
We can solve for y and z in the second and third equations and then plug into the first to solve.
x + (1/3)x + 2x = 180
3\[x + (1/3)x + 2x = 180\]
3x + x + 6x = 540
10x = 540
x = 54
y = 18
z = 108
Compare your answer with the correct one above

In the picture above,  is a straight line segment. Find the value of
is a straight line segment. Find the value of  .
.

In the picture above, 

A straight line segment has 180 degrees. Therefore, the angle that is not labelled must have:

We know that the sum of the angles in a triangle is 180 degrees. As a result, we can set up the following algebraic equation:

Subtract 70 from both sides:

Divide by 2:

A straight line segment has 180 degrees. Therefore, the angle that is not labelled must have:
We know that the sum of the angles in a triangle is 180 degrees. As a result, we can set up the following algebraic equation:
Subtract 70 from both sides:
Divide by 2:
Compare your answer with the correct one above
Solve each problem and decide which is the best of the choices given.
Solve for  .
.

Solve each problem and decide which is the best of the choices given.
Solve for 

To solve for  , you must first solve for
, you must first solve for  .
.
All triangles' angles add up to  .
.
So subtract  from
from  to get
to get  , the value of
, the value of  .
.
Angles  and
and  are supplementary, meaning they add up to
are supplementary, meaning they add up to  .
.
Subtract  from
from  to get
to get  .
.
 , so
, so  .
.
To solve for 

All triangles' angles add up to 
So subtract 



Angles 


Subtract 




Compare your answer with the correct one above
If  ,
,  , and
, and  are measures of three angles of a triangle, what is the value of
are measures of three angles of a triangle, what is the value of  ?
?
If 



Since the sum of the angles of a triangle is  , we know that
, we know that
 .
.
So



and  .
.
Since the sum of the angles of a triangle is 

So
and 
Compare your answer with the correct one above

Figure is not drawn to scale.
Refer to the provided figure. Evaluate  .
.

Figure is not drawn to scale.
Refer to the provided figure. Evaluate 
 is an equilateral, so all of its angles - in particular,
is an equilateral, so all of its angles - in particular,  - measure
- measure  . This angle is an exterior angle to
. This angle is an exterior angle to  , and its measure is equal to the sum of those of its two remote interior angles,
, and its measure is equal to the sum of those of its two remote interior angles,  and
and  , so
, so

Setting  and
and  , solve for
, solve for  :
:








Setting 


Compare your answer with the correct one above

Refer to the above figure. Evaluate  .
.

Refer to the above figure. Evaluate 
 is marked with three congruent sides, making it an equilateral triangle, so
is marked with three congruent sides, making it an equilateral triangle, so  . This is an exterior angle of
. This is an exterior angle of  , making its measure the sum of those of its remote interior angles; that is,
, making its measure the sum of those of its remote interior angles; that is,

 has congruent sides
has congruent sides  and
and  , so, by the Isosceles Triangle Theorem,
, so, by the Isosceles Triangle Theorem,  . Substituting
. Substituting  for
for  and
and  for
for  :
:



 and
and  form a linear pair and are therefore supplementary - that is, their degree measures total
form a linear pair and are therefore supplementary - that is, their degree measures total  . Setting up the equation
. Setting up the equation

and substituting:
















and substituting:
Compare your answer with the correct one above
 and
and  are similar triangles. The perimeter of Triangle A is 45” and the length of two of its sides are 15” and 10”. If the perimeter of Triangle B is 135” and what are lengths of two of its sides?
are similar triangles. The perimeter of Triangle A is 45” and the length of two of its sides are 15” and 10”. If the perimeter of Triangle B is 135” and what are lengths of two of its sides?


The perimeter is equal to the sum of the three sides. In similar triangles, each side is in proportion to its correlating side. The perimeters are also in equal proportion.
Perimeter A = 45” and perimeter B = 135”
The proportion of Perimeter A to Perimeter B is 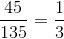 .
.
This applies to the sides of the triangle. Therefore to get the any side of Triangle B, just multiply the correlating side by 3.
15” x 3 = 45”
10” x 3 = 30“

The perimeter is equal to the sum of the three sides. In similar triangles, each side is in proportion to its correlating side. The perimeters are also in equal proportion.
Perimeter A = 45” and perimeter B = 135”
The proportion of Perimeter A to Perimeter B is 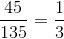
This applies to the sides of the triangle. Therefore to get the any side of Triangle B, just multiply the correlating side by 3.
15” x 3 = 45”
10” x 3 = 30“

Compare your answer with the correct one above
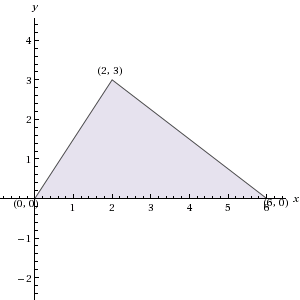
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
If  *
* , then the length of
, then the length of  must be
must be 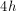 .
.
Using the formula for the area of a triangle ( ), with
), with  , the area of the triangle must be
, the area of the triangle must be  .
.
If 


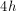
Using the formula for the area of a triangle (


Compare your answer with the correct one above
Find the height of a triangle if the area of the triangle = 18 and the base = 4.
Find the height of a triangle if the area of the triangle = 18 and the base = 4.
The area of a triangle = (1/2)bh where b is base and h is height. 18 = (1/2)4h which gives us 36 = 4h so h =9.
The area of a triangle = (1/2)bh where b is base and h is height. 18 = (1/2)4h which gives us 36 = 4h so h =9.
Compare your answer with the correct one above
Two sides of a triangle have lengths 4 and 7. Which of the following represents the set of all possible lengths of the third side, x?
Two sides of a triangle have lengths 4 and 7. Which of the following represents the set of all possible lengths of the third side, x?
The set of possible lengths is: 7-4 < x < 7+4, or 3 < X < 11.
The set of possible lengths is: 7-4 < x < 7+4, or 3 < X < 11.
Compare your answer with the correct one above
If two sides of a triangle have lengths 8 and 10, what could the length of the third side NOT be?
If two sides of a triangle have lengths 8 and 10, what could the length of the third side NOT be?
According to the Triangle Inequality Theorem, the sums of the lengths of any two sides of a triangle must be greater than the length of the third side. Since 10 + 8 is 18, the only length out of the answer choices that is not possible is 19.
According to the Triangle Inequality Theorem, the sums of the lengths of any two sides of a triangle must be greater than the length of the third side. Since 10 + 8 is 18, the only length out of the answer choices that is not possible is 19.
Compare your answer with the correct one above
A triangle has sides of length 8, 13, and L. Which of the following cannot equal L?
A triangle has sides of length 8, 13, and L. Which of the following cannot equal L?
The sum of the lengths of two sides of a triangle cannot be less than the length of the third side. 8 + 4 = 12, which is less than 13.
The sum of the lengths of two sides of a triangle cannot be less than the length of the third side. 8 + 4 = 12, which is less than 13.
Compare your answer with the correct one above
Two sides of a triangle are 20 and 32. Which of the following CANNOT be the third side of this triangle.
Two sides of a triangle are 20 and 32. Which of the following CANNOT be the third side of this triangle.
Please remember the Triangle Inequality Theorem, which states that the sum of any two sides of a triangle must be greater than the third side. Therefore, the correct answer is 10 because the sum of 10 and 20 would not be greater than the third side 32.
Please remember the Triangle Inequality Theorem, which states that the sum of any two sides of a triangle must be greater than the third side. Therefore, the correct answer is 10 because the sum of 10 and 20 would not be greater than the third side 32.
Compare your answer with the correct one above
A triangle has sides of length 5, 7, and x. Which of the following can NOT be a value of x?
A triangle has sides of length 5, 7, and x. Which of the following can NOT be a value of x?
The sum of the lengths of any two sides of a triangle must exceed the length of the third side; therefore, 5+7 > x, which cannot happen if x = 13.
The sum of the lengths of any two sides of a triangle must exceed the length of the third side; therefore, 5+7 > x, which cannot happen if x = 13.
Compare your answer with the correct one above
The lengths of two sides of a triangle are 9 and 7. Which of the following could be the length of the third side?
The lengths of two sides of a triangle are 9 and 7. Which of the following could be the length of the third side?
Let us call the third side x. According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be larger than the other two sides. Thus, all of the following must be true:
x + 7 > 9
x + 9 > 7
7 + 9 > x
We can solve these three inequalities to determine the possible values of x.
x + 7 > 9
Subtract 7 from both sides.
x > 2
Now, we can look at x + 9 > 7. Subtracting 9 from both sides, we obtain
x > –2
Finally, 7 + 9 > x, which means that 16 > x.
Therefore, x must be greater than 2, greater than –2, but also less than 16. The only number that satisfies all of these requirements is 12.
The answer is 12.
Let us call the third side x. According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be larger than the other two sides. Thus, all of the following must be true:
x + 7 > 9
x + 9 > 7
7 + 9 > x
We can solve these three inequalities to determine the possible values of x.
x + 7 > 9
Subtract 7 from both sides.
x > 2
Now, we can look at x + 9 > 7. Subtracting 9 from both sides, we obtain
x > –2
Finally, 7 + 9 > x, which means that 16 > x.
Therefore, x must be greater than 2, greater than –2, but also less than 16. The only number that satisfies all of these requirements is 12.
The answer is 12.
Compare your answer with the correct one above
The lengths of a triangle are 8, 12, and x. Which of the following inequalities shows all of the possible values of x?
The lengths of a triangle are 8, 12, and x. Which of the following inequalities shows all of the possible values of x?
According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be greater (not greater than or equal) than the remaining side. Thus, the following inequalities must all be true:
x + 8 > 12
x + 12 > 8
8 + 12 > x
Let's solve each inequality.
x + 8 > 12
Subtract 8 from both sides.
x > 4
Next, let's look at the inequality x + 12 > 8
x + 12 > 8
Subtract 12 from both sides.
x > –4
Lastly, 8 + 12 > x, which means that x < 20.
This means that x must be less than twenty, but greater than 4 and greater than –4. Since any number greater than 4 is also greater than –4, we can exclude the inequality x > –4.
To summarize, x must be greater than 4 and less than 20. We can write this as 4 < x < 20.
The answer is 4 < x < 20.
According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be greater (not greater than or equal) than the remaining side. Thus, the following inequalities must all be true:
x + 8 > 12
x + 12 > 8
8 + 12 > x
Let's solve each inequality.
x + 8 > 12
Subtract 8 from both sides.
x > 4
Next, let's look at the inequality x + 12 > 8
x + 12 > 8
Subtract 12 from both sides.
x > –4
Lastly, 8 + 12 > x, which means that x < 20.
This means that x must be less than twenty, but greater than 4 and greater than –4. Since any number greater than 4 is also greater than –4, we can exclude the inequality x > –4.
To summarize, x must be greater than 4 and less than 20. We can write this as 4 < x < 20.
The answer is 4 < x < 20.
Compare your answer with the correct one above
 , of triangle
, of triangle  in the figure is one-fourth the length of
in the figure is one-fourth the length of  . In terms of h, what is the area of triangle
. In terms of h, what is the area of triangle  ?
?