Spheres - SAT Math
Card 0 of 20
Find the diameter of a sphere with a surface area of  .
.
Find the diameter of a sphere with a surface area of 
Write the formula to find the surface area of a sphere.

Substitute the area and solve for the radius.



The diameter is double the radius.

Write the formula to find the surface area of a sphere.
Substitute the area and solve for the radius.
The diameter is double the radius.
Compare your answer with the correct one above
What is the diameter of a sphere if the surface area is  ?
?
What is the diameter of a sphere if the surface area is 
Write the formula for the surface area of a sphere.

Substitute the area and find the radius.



The diameter is double the radius.

Write the formula for the surface area of a sphere.
Substitute the area and find the radius.
The diameter is double the radius.
Compare your answer with the correct one above
What is the diameter of a sphere with a volume of  ?
?
What is the diameter of a sphere with a volume of 
Write the formula for the volume of a sphere.

Substitute the volume.

Multiply by  on both sides in order to isolate the
on both sides in order to isolate the  term.
term.


Cube root both sides.
![\sqrt[3]{\frac{9}{\pi}}= r](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/574190/gif.latex)
The diameter is double the radius.
![d= 2\sqrt[3]{\frac{9}{\pi}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/574191/gif.latex)
The answer is: ![2\sqrt[3]{\frac{9}{\pi}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/574192/gif.latex)
Write the formula for the volume of a sphere.
Substitute the volume.
Multiply by 

Cube root both sides.
The diameter is double the radius.
The answer is:
Compare your answer with the correct one above
A cube with volume 27 cubic inches is inscribed inside a sphere such that each vertex of the cube touches the sphere. What is the radius, in inches, of the sphere?
A cube with volume 27 cubic inches is inscribed inside a sphere such that each vertex of the cube touches the sphere. What is the radius, in inches, of the sphere?
We know that the cube has a volume of 27 cubic inches, so each side of the cube must be ∛27=3 inches. Since the cube is inscribed inside the sphere, the diameter of the sphere is the diagonal length of the cube, so the radius of the sphere is half of the diagonal length of the cube. To find the diagonal length of the cube, we use the distance formula d=√(32+32+32 )=√(3*32 )=3√3, and then divide the result by 2 to find the radius of the sphere, (3√3)/2.
We know that the cube has a volume of 27 cubic inches, so each side of the cube must be ∛27=3 inches. Since the cube is inscribed inside the sphere, the diameter of the sphere is the diagonal length of the cube, so the radius of the sphere is half of the diagonal length of the cube. To find the diagonal length of the cube, we use the distance formula d=√(32+32+32 )=√(3*32 )=3√3, and then divide the result by 2 to find the radius of the sphere, (3√3)/2.
Compare your answer with the correct one above
The surface area of a sphere is 100π square feet. What is the radius in feet?
The surface area of a sphere is 100π square feet. What is the radius in feet?
S = 4π(r2)
100π = 4π(r2)
100 = 4r2
25 = r2
5 = r
S = 4π(r2)
100π = 4π(r2)
100 = 4r2
25 = r2
5 = r
Compare your answer with the correct one above
What is the radius of a sphere with a surface area of 16?
What is the radius of a sphere with a surface area of 16?
In order to find the radius, first write the surface area formula for a sphere and substitute the surface area.


Divide by  on both sides in order to isolate the
on both sides in order to isolate the  term.
term.

Simplify both sides of the equation.

Square root both sides.

The radius is  .
.
In order to find the radius, first write the surface area formula for a sphere and substitute the surface area.
Divide by 

Simplify both sides of the equation.
Square root both sides.
The radius is 
Compare your answer with the correct one above
The volume of a sphere is 2304_π_ in3. What is the surface area of this sphere in square inches?
The volume of a sphere is 2304_π_ in3. What is the surface area of this sphere in square inches?
To solve this, we must first begin by finding the radius of the sphere. To do this, recall that the volume of a sphere is:
V = (4/3)_πr_3
For our data, we can say:
2304_π_ = (4/3)_πr_3; 2304 = (4/3)_r_3; 6912 = 4_r_3; 1728 = _r_3; 12 * 12 * 12 = _r_3; r = 12
Now, based on this, we can ascertain the surface area using the equation:
A = 4_πr_2
For our data, this is:
A = 4_π_*122 = 576_π_
To solve this, we must first begin by finding the radius of the sphere. To do this, recall that the volume of a sphere is:
V = (4/3)_πr_3
For our data, we can say:
2304_π_ = (4/3)_πr_3; 2304 = (4/3)_r_3; 6912 = 4_r_3; 1728 = _r_3; 12 * 12 * 12 = _r_3; r = 12
Now, based on this, we can ascertain the surface area using the equation:
A = 4_πr_2
For our data, this is:
A = 4_π_*122 = 576_π_
Compare your answer with the correct one above
A sphere has its center at the origin. A point on its surface is found on the x-y axis at (6,8). In square units, what is the surface area of this sphere?
A sphere has its center at the origin. A point on its surface is found on the x-y axis at (6,8). In square units, what is the surface area of this sphere?
To find the surface area, we must first find the radius. Based on our description, this passes from (0,0) to (6,8). This can be found using the distance formula:
62 + 82 = _r_2; _r_2 = 36 + 64; _r_2 = 100; r = 10
It should be noted that you could have quickly figured this out by seeing that (6,8) is the hypotenuse of a 6-8-10 triangle (which is a multiple of the "easy" 3-4-5).
The rest is easy. The surface area of the sphere is defined by:
A = 4_πr_2 = 4 * 100 * π = 400_π_
To find the surface area, we must first find the radius. Based on our description, this passes from (0,0) to (6,8). This can be found using the distance formula:
62 + 82 = _r_2; _r_2 = 36 + 64; _r_2 = 100; r = 10
It should be noted that you could have quickly figured this out by seeing that (6,8) is the hypotenuse of a 6-8-10 triangle (which is a multiple of the "easy" 3-4-5).
The rest is easy. The surface area of the sphere is defined by:
A = 4_πr_2 = 4 * 100 * π = 400_π_
Compare your answer with the correct one above
A spherical orange fits snugly inside a small cubical box such that each of the six walls of the box just barely touches the surface of the orange. If the volume of the box is 64 cubic inches, what is the surface area of the orange in square inches?
A spherical orange fits snugly inside a small cubical box such that each of the six walls of the box just barely touches the surface of the orange. If the volume of the box is 64 cubic inches, what is the surface area of the orange in square inches?
The volume of a cube is found by V = s3. Since V = 64, s = 4. The side of the cube is the same as the diameter of the sphere. Since d = 4, r = 2. The surface area of a sphere is found by SA = 4π(r2) = 4π(22) = 16π.
The volume of a cube is found by V = s3. Since V = 64, s = 4. The side of the cube is the same as the diameter of the sphere. Since d = 4, r = 2. The surface area of a sphere is found by SA = 4π(r2) = 4π(22) = 16π.
Compare your answer with the correct one above
A solid sphere is cut in half to form two solid hemispheres. What is the ratio of the surface area of one of the hemispheres to the surface area of the entire sphere before it was cut?
A solid sphere is cut in half to form two solid hemispheres. What is the ratio of the surface area of one of the hemispheres to the surface area of the entire sphere before it was cut?
The surface area of the sphere before it was cut is equal to the following:
surface area of solid sphere = 4_πr_2, where r is the length of the radius.
Each hemisphere will have the following shape:
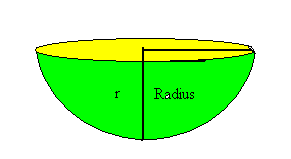
In order to determine the surface area of the hemisphere, we must find the surface area of the flat region and the curved region. The flat region will have a surface area equal to the area of a circle with radius r.
area of flat part of hemisphere = _πr_2
The surface area of the curved portion of the hemisphere will equal one-half of the surface area of the uncut sphere, which we established to be 4_πr_2.
area of curved part of hemisphere = (1/2)4_πr_2 = 2_πr_2
The total surface area of the hemisphere will be equal to the sum of the surface areas of the flat part and curved part of the hemisphere.
total surface area of hemisphere = _πr_2 + 2_πr_2 = 3_πr_2
Finally, we must find the ratio of the surface area of the hemisphere to the surface area of the uncut sphere.
ratio = (3_πr_2)/(4_πr_2) = 3/4
The answer is 3/4.
The surface area of the sphere before it was cut is equal to the following:
surface area of solid sphere = 4_πr_2, where r is the length of the radius.
Each hemisphere will have the following shape:
In order to determine the surface area of the hemisphere, we must find the surface area of the flat region and the curved region. The flat region will have a surface area equal to the area of a circle with radius r.
area of flat part of hemisphere = _πr_2
The surface area of the curved portion of the hemisphere will equal one-half of the surface area of the uncut sphere, which we established to be 4_πr_2.
area of curved part of hemisphere = (1/2)4_πr_2 = 2_πr_2
The total surface area of the hemisphere will be equal to the sum of the surface areas of the flat part and curved part of the hemisphere.
total surface area of hemisphere = _πr_2 + 2_πr_2 = 3_πr_2
Finally, we must find the ratio of the surface area of the hemisphere to the surface area of the uncut sphere.
ratio = (3_πr_2)/(4_πr_2) = 3/4
The answer is 3/4.
Compare your answer with the correct one above
A sphere is perfectly contained within a cube that has a surface area of 726 square units. In square units, what is the surface area of the sphere?
A sphere is perfectly contained within a cube that has a surface area of 726 square units. In square units, what is the surface area of the sphere?
To begin, we must determine the dimensions of the cube. To do this, recall that the surface area of a cube is made up of six squares and is thus defined as: A = 6_s_2, where s is one of the sides of the cube. For our data, this gives us:
726 = 6_s_2; 121 = _s_2; s = 11
Now, if the sphere is contained within the cube, that means that 11 represents the diameter of the sphere. Therefore, the radius of the sphere is 5.5 units. The surface area of a sphere is defined as: A = 4_πr_2. For our data, that would be:
A = 4_π_ * 5.52 = 30.25 * 4 * π = 121_π_
To begin, we must determine the dimensions of the cube. To do this, recall that the surface area of a cube is made up of six squares and is thus defined as: A = 6_s_2, where s is one of the sides of the cube. For our data, this gives us:
726 = 6_s_2; 121 = _s_2; s = 11
Now, if the sphere is contained within the cube, that means that 11 represents the diameter of the sphere. Therefore, the radius of the sphere is 5.5 units. The surface area of a sphere is defined as: A = 4_πr_2. For our data, that would be:
A = 4_π_ * 5.52 = 30.25 * 4 * π = 121_π_
Compare your answer with the correct one above
The area of a circle with radius 4 divided by the surface area of a sphere with radius 2 is equal to:
The area of a circle with radius 4 divided by the surface area of a sphere with radius 2 is equal to:
The surface area of a sphere is 4_πr_2. The area of a circle is _πr_2. 16/16 is equal to 1.
The surface area of a sphere is 4_πr_2. The area of a circle is _πr_2. 16/16 is equal to 1.
Compare your answer with the correct one above
What is the ratio of the surface area of a cube to the surface area of a sphere inscribed within it?
What is the ratio of the surface area of a cube to the surface area of a sphere inscribed within it?
Let's call the radius of the sphere r. The formula for the surface area of a sphere (A) is given below:
A = 4_πr_2
Because the sphere is inscribed inside the cube, the diameter of the sphere is equal to the side length of the cube. Because the diameter is twice the length of the radius, the diameter of the sphere is 2_r_. This means that the side length of the cube is also 2_r_.
The surface area for a cube is given by the following formula, where s represents the length of each side of the cube:
surface area of cube = 6_s_2
The formula for surface area of a cube comes from the fact that each face of the cube has an area of _s_2, and there are 6 faces total on a cube.
Since we already determined that the side length of the cube is the same as 2_r_, we can replace s with 2_r_.
surface area of cube = 6(2_r_)2 = 6(2_r_)(2_r_) = 24_r_2.
We are asked to find the ratio of the surface area of the cube to the surface area of the sphere. This means we must divide the surface area of the cube by the surface area of the sphere.
ratio = (24_r_2)/(4_πr_2)
The _r_2 term cancels in the numerator and denominator. Also, 24/4 simplifes to 6.
ratio = (24_r_2)/(4_πr_2) = 6/π
The answer is 6/π.
Let's call the radius of the sphere r. The formula for the surface area of a sphere (A) is given below:
A = 4_πr_2
Because the sphere is inscribed inside the cube, the diameter of the sphere is equal to the side length of the cube. Because the diameter is twice the length of the radius, the diameter of the sphere is 2_r_. This means that the side length of the cube is also 2_r_.
The surface area for a cube is given by the following formula, where s represents the length of each side of the cube:
surface area of cube = 6_s_2
The formula for surface area of a cube comes from the fact that each face of the cube has an area of _s_2, and there are 6 faces total on a cube.
Since we already determined that the side length of the cube is the same as 2_r_, we can replace s with 2_r_.
surface area of cube = 6(2_r_)2 = 6(2_r_)(2_r_) = 24_r_2.
We are asked to find the ratio of the surface area of the cube to the surface area of the sphere. This means we must divide the surface area of the cube by the surface area of the sphere.
ratio = (24_r_2)/(4_πr_2)
The _r_2 term cancels in the numerator and denominator. Also, 24/4 simplifes to 6.
ratio = (24_r_2)/(4_πr_2) = 6/π
The answer is 6/π.
Compare your answer with the correct one above
What is the surface area of a hemisphere with a diameter of  ?
?
What is the surface area of a hemisphere with a diameter of 
A hemisphere is half of a sphere. The surface area is broken into two parts: the spherical part and the circular base.
The surface area of a sphere is given by  .
.
So the surface area of the spherical part of a hemisphere is  .
.
The area of the circular base is given by  . The radius to use is half the diameter, or 2 cm.
. The radius to use is half the diameter, or 2 cm.
A hemisphere is half of a sphere. The surface area is broken into two parts: the spherical part and the circular base.
The surface area of a sphere is given by 
So the surface area of the spherical part of a hemisphere is 
The area of the circular base is given by 
Compare your answer with the correct one above
Six spheres have surface areas that form an arithmetic sequence. The two smallest spheres have radii 4 and 6. Give the surface area of the largest sphere.
Six spheres have surface areas that form an arithmetic sequence. The two smallest spheres have radii 4 and 6. Give the surface area of the largest sphere.
The surface area of a sphere with radius  can be determined using the formula
can be determined using the formula
 .
.
The smallest sphere, with radius  , has surface area
, has surface area

The second-smallest sphere, with radius  , has surface area
, has surface area

The surface areas are in an arithmetic sequence; their common difference is the difference of these two surface areas, or

Since the six surface areas are in an arithmetic sequence, the surface area of the largest of the six spheres - that is, the sixth-smallest sphere - is




The surface area of a sphere with radius 

The smallest sphere, with radius 
The second-smallest sphere, with radius 
The surface areas are in an arithmetic sequence; their common difference is the difference of these two surface areas, or
Since the six surface areas are in an arithmetic sequence, the surface area of the largest of the six spheres - that is, the sixth-smallest sphere - is
Compare your answer with the correct one above
The radii of six spheres form an arithmetic sequence. The smallest and largest spheres have radii 10 and 30, respectively. Give the surface area of the second-smallest sphere.
The radii of six spheres form an arithmetic sequence. The smallest and largest spheres have radii 10 and 30, respectively. Give the surface area of the second-smallest sphere.
The radii of the spheres form an arithmetic sequence, with
 and
and 
The common difference  can be computed as follows:
can be computed as follows:




The second-smallest sphere has radius

The surface area of a sphere with radius  can be determined using the formula
can be determined using the formula
 .
.
Setting  , we get
, we get
 .
.
The radii of the spheres form an arithmetic sequence, with

The common difference 
The second-smallest sphere has radius
The surface area of a sphere with radius 

Setting 

Compare your answer with the correct one above
Find the surface area of a sphere with radius 1.
Find the surface area of a sphere with radius 1.
To solve, use the formula for the surface are a of a sphere.
Substitute in the radius of one into the following equation.
Thus,

To solve, use the formula for the surface are a of a sphere.
Substitute in the radius of one into the following equation.
Thus,
Compare your answer with the correct one above
Find the surface area of a sphere whose radius is 5.
Find the surface area of a sphere whose radius is 5.
To solve, simply use the formula for the surface area of a sphere. Thus,

To solve, simply use the formula for the surface area of a sphere. Thus,
Compare your answer with the correct one above
Find the surface area of a sphere with radius 4.
Find the surface area of a sphere with radius 4.
To solve, simply use the formula for the surface area of a sphere. Thus,

The surface area for a sphere is one of those formulas you are going to have to memorize. There isn't exactly an easy wasy to derive it. My only trick for differentiating it from other circular formulas is the fact that area is two-dimensional, so you only square the r, not cube it.
To solve, simply use the formula for the surface area of a sphere. Thus,
The surface area for a sphere is one of those formulas you are going to have to memorize. There isn't exactly an easy wasy to derive it. My only trick for differentiating it from other circular formulas is the fact that area is two-dimensional, so you only square the r, not cube it.
Compare your answer with the correct one above
The surface area of a given sphere is  . What is the radius of the sphere?
. What is the radius of the sphere?
The surface area of a given sphere is 
The surface area of a given sphere is represented by the equation

Substituting in our given surface area, we can simplify this equation and solve for r.



The surface area of a given sphere is represented by the equation
Substituting in our given surface area, we can simplify this equation and solve for r.
Compare your answer with the correct one above