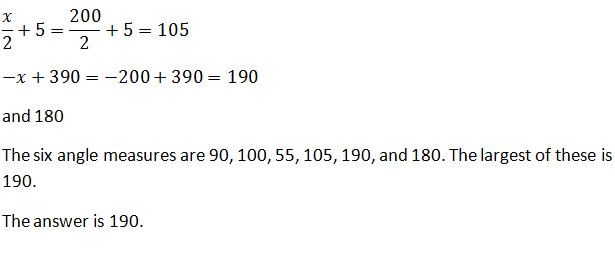Hexagons - SAT Math
Card 0 of 11
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
The sum of the interior angles of a polygon is given by  where
where  = number of sides of the polygon. An octagon has 8 sides, so the formula becomes
= number of sides of the polygon. An octagon has 8 sides, so the formula becomes 
The sum of the interior angles of a polygon is given by 

Compare your answer with the correct one above
Find the sum of all the inner angles in a hexagon.
Find the sum of all the inner angles in a hexagon.
To solve, simply use the formula to find the total degrees inside a polygon, where n is the number of vertices.
In this particular case, a hexagon means a shape with six sides and thus six vertices.
Thus,

To solve, simply use the formula to find the total degrees inside a polygon, where n is the number of vertices.
In this particular case, a hexagon means a shape with six sides and thus six vertices.
Thus,
Compare your answer with the correct one above
Calculate the approximate area a regular hexagon with the following side length:

Calculate the approximate area a regular hexagon with the following side length:
How do you find the area of a hexagon?
There are several ways to find the area of a hexagon.
- In a regular hexagon, split the figure into triangles.
- Find the area of one triangle.
- Multiply this value by six.
Alternatively, the area can be found by calculating one-half of the side length times the apothem.
Regular hexagons:
Regular hexagons are interesting polygons. Hexagons are six sided figures and possess the following shape:
In a regular hexagon, all sides equal the same length and all interior angles have the same measure; therefore, we can write the following expression.

One of the easiest methods that can be used to find the area of a polygon is to split the figure into triangles. Let's start by splitting the hexagon into six triangles.

In this figure, the center point,  , is equidistant from all of the vertices. As a result, the six dotted lines within the hexagon are the same length. Likewise, all of the triangles within the hexagon are congruent by the side-side-side rule: each of the triangle's share two sides inside the hexagon as well as a base side that makes up the perimeter of the hexagon. In a similar fashion, each of the triangles have the same angles. There are
, is equidistant from all of the vertices. As a result, the six dotted lines within the hexagon are the same length. Likewise, all of the triangles within the hexagon are congruent by the side-side-side rule: each of the triangle's share two sides inside the hexagon as well as a base side that makes up the perimeter of the hexagon. In a similar fashion, each of the triangles have the same angles. There are  in a circle and the hexagon in our image has separated it into six equal parts; therefore, we can write the following:
in a circle and the hexagon in our image has separated it into six equal parts; therefore, we can write the following:



We also know the following:

Now, let's look at each of the triangles in the hexagon. We know that each triangle has two two sides that are equal; therefore, each of the base angles of each triangle must be the same. We know that a triangle has  and we can solve for the two base angles of each triangle using this information.
and we can solve for the two base angles of each triangle using this information.



Each angle in the triangle equals  . We now know that all the triangles are congruent and equilateral: each triangle has three equal side lengths and three equal angles. Now, we can use this vital information to solve for the hexagon's area. If we find the area of one of the triangles, then we can multiply it by six in order to calculate the area of the entire figure. Let's start by analyzing
. We now know that all the triangles are congruent and equilateral: each triangle has three equal side lengths and three equal angles. Now, we can use this vital information to solve for the hexagon's area. If we find the area of one of the triangles, then we can multiply it by six in order to calculate the area of the entire figure. Let's start by analyzing  . If we draw, an altitude through the triangle, then we find that we create two
. If we draw, an altitude through the triangle, then we find that we create two  triangles.
triangles.

Let's solve for the length of this triangle. Remember that in  triangles, triangles possess side lengths in the following ratio:
triangles, triangles possess side lengths in the following ratio:

Now, we can analyze  using the a substitute variable for side length,
using the a substitute variable for side length,  .
.

We know the measure of both the base and height of  and we can solve for its area.
and we can solve for its area.



Now, we need to multiply this by six in order to find the area of the entire hexagon.
![\textup{Area of Hexagon}[ABCDEF]=6\times\frac{\sqrt{3}s^2}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065143/gif.latex)
![\textup{Area of Hexagon}[ABCDEF]=\frac{6 \sqrt{3}s^2}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065144/gif.latex)
![\textup{Area of Hexagon}[ABCDEF]=\frac{3\sqrt{3}}{2}\times s^2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065145/gif.latex)
We have solved for the area of a regular hexagon with side length,  . If we know the side length of a regular hexagon, then we can solve for the area.
. If we know the side length of a regular hexagon, then we can solve for the area.
If we are not given a regular hexagon, then we an solve for the area of the hexagon by using the side length(i.e.  ) and apothem (i.e.
) and apothem (i.e.  ), which is the length of a line drawn from the center of the polygon to the right angle of any side. This is denoted by the variable
), which is the length of a line drawn from the center of the polygon to the right angle of any side. This is denoted by the variable  in the following figure:
in the following figure:

Alternative method:
If we are given the variables  and
and  , then we can solve for the area of the hexagon through the following formula:
, then we can solve for the area of the hexagon through the following formula:

In this equation,  is the area,
is the area,  is the perimeter, and
is the perimeter, and  is the apothem. We must calculate the perimeter using the side length and the equation
is the apothem. We must calculate the perimeter using the side length and the equation  , where
, where  is the side length.
is the side length.
Solution:
In the given problem we know that the side length of a regular hexagon is the following:

Let's substitute this value into the area formula for a regular hexagon and solve.


Simplify.



Round the answer to the nearest whole number.

How do you find the area of a hexagon?
There are several ways to find the area of a hexagon.
- In a regular hexagon, split the figure into triangles.
- Find the area of one triangle.
- Multiply this value by six.
Alternatively, the area can be found by calculating one-half of the side length times the apothem.
Regular hexagons:
Regular hexagons are interesting polygons. Hexagons are six sided figures and possess the following shape:
In a regular hexagon, all sides equal the same length and all interior angles have the same measure; therefore, we can write the following expression.
One of the easiest methods that can be used to find the area of a polygon is to split the figure into triangles. Let's start by splitting the hexagon into six triangles.

In this figure, the center point, 


We also know the following:
Now, let's look at each of the triangles in the hexagon. We know that each triangle has two two sides that are equal; therefore, each of the base angles of each triangle must be the same. We know that a triangle has 
Each angle in the triangle equals 



Let's solve for the length of this triangle. Remember that in 
Now, we can analyze 


We know the measure of both the base and height of 
Now, we need to multiply this by six in order to find the area of the entire hexagon.
We have solved for the area of a regular hexagon with side length, 
If we are not given a regular hexagon, then we an solve for the area of the hexagon by using the side length(i.e. 



Alternative method:
If we are given the variables 

In this equation, 




Solution:
In the given problem we know that the side length of a regular hexagon is the following:
Let's substitute this value into the area formula for a regular hexagon and solve.
Simplify.
Round the answer to the nearest whole number.
Compare your answer with the correct one above
An equilateral triangle with side length  has one of its vertices at the center of a regular hexagon, and the side opposite that vertex is one of the sides of the hexagon. What is the hexagon's area?
has one of its vertices at the center of a regular hexagon, and the side opposite that vertex is one of the sides of the hexagon. What is the hexagon's area?
An equilateral triangle with side length 
Because it can be split into two  triangles, the area of an equilateral triangle can be expressed as...
triangles, the area of an equilateral triangle can be expressed as...

With that in mind, the equilateral triangle in question has area of  .
.
Now consider that a regular hexagon can be split into six congruent equilateral triangles with a vertex at the center and the side opposite the center as one of the hexagon's sides (a handy way of finding a hexagon's area if you can't use the regular polygon formula requiring an apothem.) Knowing that, our answer is  .
.
Because it can be split into two 
With that in mind, the equilateral triangle in question has area of 
Now consider that a regular hexagon can be split into six congruent equilateral triangles with a vertex at the center and the side opposite the center as one of the hexagon's sides (a handy way of finding a hexagon's area if you can't use the regular polygon formula requiring an apothem.) Knowing that, our answer is 
Compare your answer with the correct one above
How many diagonals are there in a regular hexagon?
How many diagonals are there in a regular hexagon?
A diagonal connects two non-consecutive vertices of a polygon. A hexagon has six sides. There are 3 diagonals from a single vertex, and there are 6 vertices on a hexagon, which suggests there would be 18 diagonals in a hexagon. However, we must divide by two as half of the diagonals are common to the same vertices. Thus there are 9 unique diagonals in a hexagon. The formula for the number of diagonals of a polygon is:

where n = the number of sides in the polygon.
Thus a pentagon thas 5 diagonals. An octagon has 20 diagonals.
A diagonal connects two non-consecutive vertices of a polygon. A hexagon has six sides. There are 3 diagonals from a single vertex, and there are 6 vertices on a hexagon, which suggests there would be 18 diagonals in a hexagon. However, we must divide by two as half of the diagonals are common to the same vertices. Thus there are 9 unique diagonals in a hexagon. The formula for the number of diagonals of a polygon is:
where n = the number of sides in the polygon.
Thus a pentagon thas 5 diagonals. An octagon has 20 diagonals.
Compare your answer with the correct one above
How many diagonals are there in a regular hexagon?
How many diagonals are there in a regular hexagon?
A diagonal is a line segment joining two non-adjacent vertices of a polygon. A regular hexagon has six sides and six vertices. One vertex has three diagonals, so a hexagon would have three diagonals times six vertices, or 18 diagonals. Divide this number by 2 to account for duplicate diagonals between two vertices. The formula for the number of vertices in a polygon is:

where  .
.
A diagonal is a line segment joining two non-adjacent vertices of a polygon. A regular hexagon has six sides and six vertices. One vertex has three diagonals, so a hexagon would have three diagonals times six vertices, or 18 diagonals. Divide this number by 2 to account for duplicate diagonals between two vertices. The formula for the number of vertices in a polygon is:
where 
Compare your answer with the correct one above
Hexagon  is a regular hexagon with sides of length 10.
is a regular hexagon with sides of length 10.  is the midpoint of
is the midpoint of  . To the nearest tenth, give the length of the segment
. To the nearest tenth, give the length of the segment  .
.
Hexagon 



Below is the referenced hexagon, with some additional segments constructed.

Note that the segments  and
and  have been constructed. Along with
have been constructed. Along with  , they form right triangle
, they form right triangle  with hypotenuse
with hypotenuse  .
.
 is the midpoint of
is the midpoint of  , so
, so
 .
.
 has been divided by drawing the perpendicular from
has been divided by drawing the perpendicular from  to the segment and calling the point of intersection
to the segment and calling the point of intersection  .
.  is a 30-60-90 triangle with hypotenuse
is a 30-60-90 triangle with hypotenuse  , short leg
, short leg  , and long leg
, and long leg  , so by the 30-60-90 Triangle Theorem,
, so by the 30-60-90 Triangle Theorem,

and

For the same reason,  , so
, so

By the Pythagorean Theorem,




 when rounded to the nearest tenth.
when rounded to the nearest tenth.
Below is the referenced hexagon, with some additional segments constructed.

Note that the segments 














and
For the same reason, 
By the Pythagorean Theorem,

Compare your answer with the correct one above

The provided image represents a track in the shape of a regular hexagon with perimeter one fourth of a mile.
Teresa starts at Point A and runs clockwise until she gets halfway between Point E and Point F. How far does she run, in feet?

The provided image represents a track in the shape of a regular hexagon with perimeter one fourth of a mile.
Teresa starts at Point A and runs clockwise until she gets halfway between Point E and Point F. How far does she run, in feet?
One mile is equal to 5,280 feet; one fourth of a mile is equal to

Each of the six congruent sides measures one sixth of this, or

Teresa runs clockwise from Point A to halfway between Point E and Point F, so she runs along four and one half sides, for a total of

One mile is equal to 5,280 feet; one fourth of a mile is equal to
Each of the six congruent sides measures one sixth of this, or
Teresa runs clockwise from Point A to halfway between Point E and Point F, so she runs along four and one half sides, for a total of
Compare your answer with the correct one above

Archimedes High School has an unusual track in that it is shaped like a regular hexagon, as above. Each side of the hexagon measures 264 feet.
Alvin runs at a steady speed of seven miles an hour for twelve minutes, starting at point A and working his way clockwise. When he is finished, which of the following points is he closest to?

Archimedes High School has an unusual track in that it is shaped like a regular hexagon, as above. Each side of the hexagon measures 264 feet.
Alvin runs at a steady speed of seven miles an hour for twelve minutes, starting at point A and working his way clockwise. When he is finished, which of the following points is he closest to?
Alvin runs at a rate of seven miles an hour for twelve minutes, or 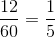 hours. The distance he runs is equal to his rate multiplied by his time, so, setting
hours. The distance he runs is equal to his rate multiplied by his time, so, setting in this formula:
in this formula:

 miles.
miles.
One mile comprises 5,280 feet, so this is equal to
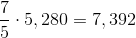 feet
feet
Since each side of the track measures 264 feet, this means that Alvin runs
 sidelengths.
sidelengths.
 ,
,
which means that Alvin runs around the track four complete times, plus four more sides of the track. Alvin stops when he is at Point E.
Alvin runs at a rate of seven miles an hour for twelve minutes, or 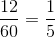


One mile comprises 5,280 feet, so this is equal to
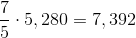
Since each side of the track measures 264 feet, this means that Alvin runs


which means that Alvin runs around the track four complete times, plus four more sides of the track. Alvin stops when he is at Point E.
Compare your answer with the correct one above
A circle with circumference 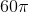 is inscribed in a regular hexagon. Give the perimeter of the hexagon.
is inscribed in a regular hexagon. Give the perimeter of the hexagon.
A circle with circumference 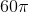
Below is the figure referenced; note that the hexagon is divided by its diameters, and that an apothem—a perpendicular bisector from the center to one side—has been drawn.

The circle has circumference  ; its radius, which coincides with the apothem of the hexagon,
; its radius, which coincides with the apothem of the hexagon,  is the circumference divided by
is the circumference divided by  :
:

The hexagon is divided into six equilateral triangles. One,  , is divided by an apothem of the hexagon
, is divided by an apothem of the hexagon  - a radius of the circle - into two 30-60-90 triangles, one of which is
- a radius of the circle - into two 30-60-90 triangles, one of which is  . Since
. Since  has length 30, and it is a long leg of
has length 30, and it is a long leg of  , then short leg
, then short leg  has length
has length

 is the midpoint of
is the midpoint of  , one of the six congruent sides of the hexagon, so
, one of the six congruent sides of the hexagon, so
 ;
;
this makes the perimeter of the hexagon six times this, or
 .
.
Below is the figure referenced; note that the hexagon is divided by its diameters, and that an apothem—a perpendicular bisector from the center to one side—has been drawn.

The circle has circumference 


The hexagon is divided into six equilateral triangles. One, 








this makes the perimeter of the hexagon six times this, or

Compare your answer with the correct one above