Circles - SAT Math
Card 0 of 20
A 6 by 8 rectangle is inscribed in a circle. What is the circumference of the circle?
A 6 by 8 rectangle is inscribed in a circle. What is the circumference of the circle?
First you must draw the diagram. The diagonal of the rectangle is also the diameter of the circle. The diagonal is the hypotenuse of a multiple of 2 of a 3,4,5 triangle, and therefore is 10.
Circumference = π * diameter = 10_π_.
First you must draw the diagram. The diagonal of the rectangle is also the diameter of the circle. The diagonal is the hypotenuse of a multiple of 2 of a 3,4,5 triangle, and therefore is 10.
Circumference = π * diameter = 10_π_.
Compare your answer with the correct one above
A circle with an area of 13_π_ in2 is centered at point C. What is the circumference of this circle?
A circle with an area of 13_π_ in2 is centered at point C. What is the circumference of this circle?
The formula for the area of a circle is A = _πr_2.
We are given the area, and by substitution we know that 13_π_ = _πr_2.
We divide out the π and are left with 13 = _r_2.
We take the square root of r to find that r = √13.
We find the circumference of the circle with the formula C = 2_πr_.
We then plug in our values to find C = 2√13_π_.
The formula for the area of a circle is A = _πr_2.
We are given the area, and by substitution we know that 13_π_ = _πr_2.
We divide out the π and are left with 13 = _r_2.
We take the square root of r to find that r = √13.
We find the circumference of the circle with the formula C = 2_πr_.
We then plug in our values to find C = 2√13_π_.
Compare your answer with the correct one above
Ashley has a square room in her apartment that measures 81 square feet. What is the circumference of the largest circular area rug that she can fit in the space?
Ashley has a square room in her apartment that measures 81 square feet. What is the circumference of the largest circular area rug that she can fit in the space?
In order to solve this question, first calculate the length of each side of the room.



The length of each side of the room is also equal to the length of the diameter of the largest circular rug that can fit in the room. Since  , the circumference is simply
, the circumference is simply

In order to solve this question, first calculate the length of each side of the room.
The length of each side of the room is also equal to the length of the diameter of the largest circular rug that can fit in the room. Since 
Compare your answer with the correct one above
A gardener wants to build a fence around their garden shown below. How many feet of fencing will they need, if the length of the rectangular side is 12 and the width is 8?

A gardener wants to build a fence around their garden shown below. How many feet of fencing will they need, if the length of the rectangular side is 12 and the width is 8?

The shape of the garden consists of a rectangle and two semi-circles. Since they are building a fence we need to find the perimeter. The perimeter of the length of the rectangle is 24. The perimeter or circumference of the circle can be found using the equation C=2π(r), where r= the radius of the circle. Since we have two semi-circles we can find the circumference of one whole circle with a radius of 4, which would be 8π.
The shape of the garden consists of a rectangle and two semi-circles. Since they are building a fence we need to find the perimeter. The perimeter of the length of the rectangle is 24. The perimeter or circumference of the circle can be found using the equation C=2π(r), where r= the radius of the circle. Since we have two semi-circles we can find the circumference of one whole circle with a radius of 4, which would be 8π.
Compare your answer with the correct one above
If a circle has an area of  , what is the circumference of the circle?
, what is the circumference of the circle?
If a circle has an area of 
The formula for the area of a circle is πr2. For this particular circle, the area is 81π, so 81π = πr2. Divide both sides by π and we are left with r2=81. Take the square root of both sides to find r=9. The formula for the circumference of the circle is 2πr = 2π(9) = 18π. The correct answer is 18π.
The formula for the area of a circle is πr2. For this particular circle, the area is 81π, so 81π = πr2. Divide both sides by π and we are left with r2=81. Take the square root of both sides to find r=9. The formula for the circumference of the circle is 2πr = 2π(9) = 18π. The correct answer is 18π.
Compare your answer with the correct one above
A car tire has a radius of 18 inches. When the tire has made 200 revolutions, how far has the car gone in feet?
A car tire has a radius of 18 inches. When the tire has made 200 revolutions, how far has the car gone in feet?
If the radius is 18 inches, the diameter is 3 feet. The circumference of the tire is therefore 3π by C=d(π). After 200 revolutions, the tire and car have gone 3π x 200 = 600π feet.
If the radius is 18 inches, the diameter is 3 feet. The circumference of the tire is therefore 3π by C=d(π). After 200 revolutions, the tire and car have gone 3π x 200 = 600π feet.
Compare your answer with the correct one above
A circle has the equation below. What is the circumference of the circle?
(x – 2)2 + (y + 3)2 = 9
A circle has the equation below. What is the circumference of the circle?
(x – 2)2 + (y + 3)2 = 9
The radius is 3. Yielding a circumference of  .
.
The radius is 3. Yielding a circumference of 
Compare your answer with the correct one above
The diameter of a circle is defined by the two points (2,5) and (4,6). What is the circumference of this circle?
The diameter of a circle is defined by the two points (2,5) and (4,6). What is the circumference of this circle?
We first must calculate the distance between these two points. Recall that the distance formula is:√((x2 - x1)2 + (y2 - y1)2)
For us, it is therefore: √((4 - 2)2 + (6 - 5)2) = √((2)2 + (1)2) = √(4 + 1) = √5
If d = √5, the circumference of our circle is πd, or π√5.
We first must calculate the distance between these two points. Recall that the distance formula is:√((x2 - x1)2 + (y2 - y1)2)
For us, it is therefore: √((4 - 2)2 + (6 - 5)2) = √((2)2 + (1)2) = √(4 + 1) = √5
If d = √5, the circumference of our circle is πd, or π√5.
Compare your answer with the correct one above
Find the circumferencce fo a circle given radius of 7.
Find the circumferencce fo a circle given radius of 7.
To solve, simply use the formula for the circumference of a circle. Thus,

Like the prior question, it is important to think about dimensions if you don't remember the exact formula. Circumference is 1 dimensional, so it makes sense that the variable is not squared as cubed. If you rather, you can use the following formula, but realize by defining diameter, it equals the prior one.


Thus,

To solve, simply use the formula for the circumference of a circle. Thus,
Like the prior question, it is important to think about dimensions if you don't remember the exact formula. Circumference is 1 dimensional, so it makes sense that the variable is not squared as cubed. If you rather, you can use the following formula, but realize by defining diameter, it equals the prior one.
Thus,
Compare your answer with the correct one above
The area of a circle is  . What is its circumference?
. What is its circumference?
The area of a circle is 
First, let's find the radius r of the circle by using the given area.



Now, plug this radius into the formula for a circle's circumference.
 .
.
First, let's find the radius r of the circle by using the given area.
Now, plug this radius into the formula for a circle's circumference.

Compare your answer with the correct one above
The surface area of a sphere is  .
.
 is a point on the surface of the sphere;
is a point on the surface of the sphere;  is the point on the sphere farthest from
is the point on the sphere farthest from  . A curve is drawn from
. A curve is drawn from  to
to  entirely on the surface of the sphere. Give the length of the shortest possible curve fitting this description.
entirely on the surface of the sphere. Give the length of the shortest possible curve fitting this description.
The surface area of a sphere is 





Below is a sphere with its center  and with points
and with points  and
and  as described.
as described.

For  and
and  to be on the surface of the sphere and to be a maximum distance apart, they must be endpoints of a diameter of the sphere. The shortest curve connecting them that is entirely on the surface is a semicircle whose radius coincides with that of the sphere. Therefore, first find the radius of the sphere using the surface area formula
to be on the surface of the sphere and to be a maximum distance apart, they must be endpoints of a diameter of the sphere. The shortest curve connecting them that is entirely on the surface is a semicircle whose radius coincides with that of the sphere. Therefore, first find the radius of the sphere using the surface area formula

Setting  and solving for
and solving for  :
:




The length of the curve is half the circumference of a circle with radius 10, or

Substituting 10 for  , this is
, this is
 .
.
Below is a sphere with its center 



For 

Setting 

The length of the curve is half the circumference of a circle with radius 10, or
Substituting 10 for 

Compare your answer with the correct one above
Give the circumference of a circle with the following diameter:

Give the circumference of a circle with the following diameter:
The circumference of a circle is its diameter multiplied by  , so, since the diameter is 100, the circumference is simply
, so, since the diameter is 100, the circumference is simply  .
.
The circumference of a circle is its diameter multiplied by 

Compare your answer with the correct one above

In the circle above, the length of arc BC is 100 degrees, and the segment AC is a diameter. What is the measure of angle ADB in degrees?
In the circle above, the length of arc BC is 100 degrees, and the segment AC is a diameter. What is the measure of angle ADB in degrees?
Since we know that segment AC is a diameter, this means that the length of the arc ABC must be 180 degrees. This means that the length of the arc AB must be 80 degrees.
Since angle ADB is an inscribed angle, its measure is equal to half of the measure of the angle of the arc that it intercepts. This means that the measure of the angle is half of 80 degrees, or 40 degrees.
Since we know that segment AC is a diameter, this means that the length of the arc ABC must be 180 degrees. This means that the length of the arc AB must be 80 degrees.
Since angle ADB is an inscribed angle, its measure is equal to half of the measure of the angle of the arc that it intercepts. This means that the measure of the angle is half of 80 degrees, or 40 degrees.
Compare your answer with the correct one above
The length of an arc,  , of a circle is
, of a circle is  and the radius,
and the radius,  , of the circle is
, of the circle is  . What is the measure in degrees of the central angle,
. What is the measure in degrees of the central angle,  , formed by the arc
, formed by the arc  ?
?
The length of an arc, 





The circumference of the circle is  .
.

The length of the arc S is  .
.
A ratio can be established:


Solving for _ _yields 90o.
_yields 90o.
Note: This makes sense. Since the arc S was one-fourth the circumference of the circle, the central angle formed by arc S should be one-fourth the total degrees of a circle.
The circumference of the circle is 
The length of the arc S is 
A ratio can be established:
Solving for _
Note: This makes sense. Since the arc S was one-fourth the circumference of the circle, the central angle formed by arc S should be one-fourth the total degrees of a circle.
Compare your answer with the correct one above
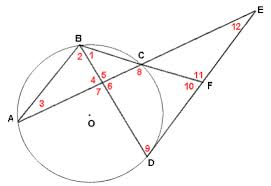
In the figure above that includes Circle O, the measure of angle BAC is equal to 35 degrees, the measure of angle FBD is equal to 40 degrees, and the measure of arc AD is twice the measure of arc AB. Which of the following is the measure of angle CEF? The figure is not necessarily drawn to scale, and the red numbers are used to mark the angles, not represent angle measures.

In the figure above that includes Circle O, the measure of angle BAC is equal to 35 degrees, the measure of angle FBD is equal to 40 degrees, and the measure of arc AD is twice the measure of arc AB. Which of the following is the measure of angle CEF? The figure is not necessarily drawn to scale, and the red numbers are used to mark the angles, not represent angle measures.
The measure of angle CEF is going to be equal to half of the difference between the measures two arcs that it intercepts, namely arcs AD and CD.

Thus, we need to find the measure of arcs AD and CD. Let's look at the information given and determine how it can help us figure out the measures of arcs AD and CD.
Angle BAC is an inscribed angle, which means that its meausre is one-half of the measure of the arc that it incercepts, which is arc BC.


Thus, since angle BAC is 35 degrees, the measure of arc BC must be 70 degrees.
We can use a similar strategy to find the measure of arc CD, which is the arc intercepted by the inscribed angle FBD.

Because angle FBD has a measure of 40 degrees, the measure of arc CD must be 80 degrees.
We have the measures of arcs BC and CD. But we still need the measure of arc AD. We can use the last piece of information given, along with our knowledge about the sum of the arcs of a circle, to determine the measure of arc AD.
We are told that the measure of arc AD is twice the measure of arc AB. We also know that the sum of the measures of arcs AD, AB, CD, and BC must be 360 degrees, because there are 360 degrees in a full circle.



Because AD = 2AB, we can substitute 2AB for AD.



This means the measure of arc AB is 70 degrees, and the measure of arc AD is 2(70) = 140 degrees.
Now, we have all the information we need to find the measure of angle CEF, which is equal to half the difference between the measure of arcs AD and CD.



The measure of angle CEF is going to be equal to half of the difference between the measures two arcs that it intercepts, namely arcs AD and CD.
Thus, we need to find the measure of arcs AD and CD. Let's look at the information given and determine how it can help us figure out the measures of arcs AD and CD.
Angle BAC is an inscribed angle, which means that its meausre is one-half of the measure of the arc that it incercepts, which is arc BC.
Thus, since angle BAC is 35 degrees, the measure of arc BC must be 70 degrees.
We can use a similar strategy to find the measure of arc CD, which is the arc intercepted by the inscribed angle FBD.
Because angle FBD has a measure of 40 degrees, the measure of arc CD must be 80 degrees.
We have the measures of arcs BC and CD. But we still need the measure of arc AD. We can use the last piece of information given, along with our knowledge about the sum of the arcs of a circle, to determine the measure of arc AD.
We are told that the measure of arc AD is twice the measure of arc AB. We also know that the sum of the measures of arcs AD, AB, CD, and BC must be 360 degrees, because there are 360 degrees in a full circle.
Because AD = 2AB, we can substitute 2AB for AD.
This means the measure of arc AB is 70 degrees, and the measure of arc AD is 2(70) = 140 degrees.
Now, we have all the information we need to find the measure of angle CEF, which is equal to half the difference between the measure of arcs AD and CD.
Compare your answer with the correct one above
A pie has a diameter of 12". A piece is cut out, having a surface area of 4.5π. What is the angle of the cut?
A pie has a diameter of 12". A piece is cut out, having a surface area of 4.5π. What is the angle of the cut?
This is simply a matter of percentages. We first have to figure out what percentage of the surface area is represented by 4.5π. To do that, we must calculate the total surface area. If the diameter is 12, the radius is 6. Don't be tricked by this!
A = π * 6 * 6 = 36π
Now, 4.5π is 4.5π/36π percentage or 0.125 (= 12.5%)
To figure out the angle, we must take that percentage of 360°:
0.125 * 360 = 45°
This is simply a matter of percentages. We first have to figure out what percentage of the surface area is represented by 4.5π. To do that, we must calculate the total surface area. If the diameter is 12, the radius is 6. Don't be tricked by this!
A = π * 6 * 6 = 36π
Now, 4.5π is 4.5π/36π percentage or 0.125 (= 12.5%)
To figure out the angle, we must take that percentage of 360°:
0.125 * 360 = 45°
Compare your answer with the correct one above
Eric is riding a Ferris wheel. The Ferris wheel has 18 compartments, numbered in order clockwise. If compartment 1 is at 0 degrees and Eric enters compartment 13, what angle is he at?
Eric is riding a Ferris wheel. The Ferris wheel has 18 compartments, numbered in order clockwise. If compartment 1 is at 0 degrees and Eric enters compartment 13, what angle is he at?
12 compartments further means 240 more degrees. 240 is the answer.
360/12 = 240 degrees
12 compartments further means 240 more degrees. 240 is the answer.
360/12 = 240 degrees
Compare your answer with the correct one above
What is the angle of a sector of area 
 on a circle having a radius of
on a circle having a radius of  ?
?
What is the angle of a sector of area 


To begin, you should compute the complete area of the circle:

For your data, this is:

Now, to find the angle measure of a sector, you find what portion of the circle the sector is. Here, it is:

Now, multiply this by the total  degrees in a circle:
degrees in a circle:

Rounded, this is  .
.
To begin, you should compute the complete area of the circle:
For your data, this is:
Now, to find the angle measure of a sector, you find what portion of the circle the sector is. Here, it is:
Now, multiply this by the total 
Rounded, this is 
Compare your answer with the correct one above
What is the angle of a sector that has an arc length of 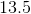
 on a circle of diameter
on a circle of diameter 
 ?
?
What is the angle of a sector that has an arc length of 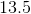



The first thing to do for this problem is to compute the total circumference of the circle. Notice that you were given the diameter. The proper equation is therefore:

For your data, this means,

Now, to compute the angle, note that you have a percentage of the total circumference, based upon your arc length:

Rounded to the nearest hundredth, this is  .
.
The first thing to do for this problem is to compute the total circumference of the circle. Notice that you were given the diameter. The proper equation is therefore:
For your data, this means,
Now, to compute the angle, note that you have a percentage of the total circumference, based upon your arc length:
Rounded to the nearest hundredth, this is 
Compare your answer with the correct one above

Figure NOT drawn to scale.
Refer to the above diagram. is a semicircle. Evaluate
is a semicircle. Evaluate  .
.

Figure NOT drawn to scale.
Refer to the above diagram.

An inscribed angle of a circle that intercepts a semicircle is a right angle; therefore,  , which intercepts the semicircle
, which intercepts the semicircle  , is such an angle. Consequently,
, is such an angle. Consequently,  , and
, and  is a right triangle. The acute angles of
is a right triangle. The acute angles of  are complementary, so
are complementary, so








The measure of inscribed  is
is
 .
.
An inscribed angle of a circle intercepts an arc of twice its degree measure, so
 .
.
An inscribed angle of a circle that intercepts a semicircle is a right angle; therefore, 




The measure of inscribed 

An inscribed angle of a circle intercepts an arc of twice its degree measure, so

Compare your answer with the correct one above



