How to find slope of a line - SAT Math

Card 0 of 20

Question

What is a possible slope of line y?

Answer

The slope is negative as it starts in quadrant 2 and ends in quadrant 4. Slope is equivlent to the change in y divided by the change in x. The change in y is greater than the change in x, which implies that the slope must be less than –1, leaving –2 as the only possible solution.

Compare your answer with the correct one above

Question

What is the slope of a line that runs through points: (-2, 5) and (1, 7)?

Answer

The slope of a line is defined as a change in the y coordinates over a change in the x coordinates (rise over run).

To calculate the slope of a line, use the following formula:

Compare your answer with the correct one above

Question

Find the slope of the line 6X – 2Y = 14

Answer

Put the equation in slope-intercept form:

y = mx + b

-2y = -6x +14

y = 3x – 7

The slope of the line is represented by M; therefore the slope of the line is 3.

Compare your answer with the correct one above

Question

A line passes through the points (–3, 5) and (2, 3). What is the slope of this line?

Answer

The slope of the line that passes these two points are simply ∆y/∆x = (3-5)/(2+3) = -2/5

Compare your answer with the correct one above

Question

What is the slope of line 3 = 8y - 4x?

Answer

Solve equation for y. y=mx+b, where m is the slope

Compare your answer with the correct one above

Question

Based on the table below, when x = 5, y will equal

x y
-1 3
0 1
1 -1
2 -3

x	y
-1	3
0	1
1	-1
2	-3

Answer

Use 2 points from the chart to find the equation of the line.

Example: (–1, 3) and (1, –1)

Using the formula for the slope, we find the slope to be –2. Putting that into our equation for a line we get y = –2x + b. Plug in one of the points for x and y into this equation in order to find b. b = 1.

The equation then will be: y = –2x + 1.

Plug in 5 for x in order to find y.

y = –2(5) + 1

y = –9

Compare your answer with the correct one above

Question

What is the slope of the given linear equation?

2x + 4y = -7

Answer

We can convert the given equation into slope-intercept form, y=mx+b, where m is the slope. We get y = (-1/2)x + (-7/2)

Compare your answer with the correct one above

Question

What is the slope of the line:

$\frac{14}{3}x=\frac{1}{6}y-7$

Answer

First put the question in slope intercept form (y = mx + b):

–(1/6)y = –(14/3)x – 7 =>

y = 6(14/3)x – 7

y = 28x – 7.

The slope is 28.

Compare your answer with the correct one above

Question

If 2x – 4y = 10, what is the slope of the line?

Answer

First put the equation into slope-intercept form, solving for y: 2x – 4y = 10 → –4y = –2x + 10 → y = 1/2*x – 5/2. So the slope is 1/2.

Compare your answer with the correct one above

Question

Which of the following lines intersects the y-axis at a thirty degree angle?

Answer

Compare your answer with the correct one above

Question

What is the slope of the line with equation 4_x_ – 16_y_ = 24?

Answer

The equation of a line is:

y = mx + b, where m is the slope

4_x_ – 16_y_ = 24

–16_y_ = –4_x_ + 24

y = (–4_x_)/(–16) + 24/(–16)

y = (1/4)x – 1.5

Slope = 1/4

Compare your answer with the correct one above

Question

What is the slope of a line which passes through coordinates $\dpi{100} \small (3,7)$ and $\dpi{100} \small (4,12)$ ?

Answer

Slope is found by dividing the difference in the $\dpi{100} \small y$ -coordinates by the difference in the $\dpi{100} \small x$ -coordinates.

$\dpi{100} \small \frac{(12-7)}{(4-3)}=\frac{5}{1}=5$

Compare your answer with the correct one above

Question

What is the slope of a line that passes though the coordinates $(5,2)$ and $(3,1)$ ?

Answer

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{1-2}{3-5}=\frac{-1}{-2}=\frac{1}{2}$

Compare your answer with the correct one above

Question

What is the slope of the line represented by the equation $6y-16x=7$ ?

Answer

To rearrange the equation into a $y=mx+b$ format, you want to isolate the $y$ so that it is the sole variable, without a coefficient, on one side of the equation.

First, add $11x$ to both sides to get $6y=7+16x$ .

Then, divide both sides by 6 to get $y=\frac{7+16x}{6}$ .

If you divide each part of the numerator by 6, you get $y=\frac{7}{6}+\frac{16x}{6}$ . This is in a $y=b+mx$ form, and the $m$ is equal to $\frac{16}{6}$ , which is reduced down to $\frac{8}{3}$ for the correct answer.

Compare your answer with the correct one above

Question

What is the slope between and ?

Answer

Let $P_{1}=(8,3)$ and $P_{2}=(5,7)$

$m = (y_{2} - y_{1}) \div (x_{2} - x_{1})$ so the slope becomes $-\frac{4}{3}$ .

Compare your answer with the correct one above

Question

What is the slope of a line running through points and ?

Answer

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

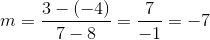
$m=\frac{3-(-4)}{7-8}=\frac{7}{-1}=-7$

Compare your answer with the correct one above

Question

Solve each problem and decide which is the best of the choices given.

Find the slope of the line for the given equation.

Answer

For this problem, you have to solve for . We want to get the equation in slope-intercept form,

where represents the slope of the line.

First subtract from each side to get

.

Then divide both sides by to get

.

The slope is the number in front of , so the slope is .

Compare your answer with the correct one above

Question

Point is at and point is at . What is the slope of the line that connects the two points?

Answer

The purpose of this question is to understand how the slope of a line is calculated.

The slope is the rise over the run, meaning the change in the y values over the change in the x values

$\frac{y_2-y_1}{x_2-x_1}$ .

So, the difference in y values divided by the difference in x values yields

$\frac{1-(-5)}{3-(-2)}=\frac{6}{5}$ .

Compare your answer with the correct one above

Question

The following two points are located on the same line. What is the slope of the line?

$(2\pi, 5\pi), (11\pi, 6\pi)$

Answer

The slope of a line with two points and is given by the following equation:

$m = \frac{y_2-y_1}{x_2-x_1}$

Let $(x_1, y_1) = (2\pi, 5\pi)$ and $(x_2, y_2) = (11\pi, 6\pi)$ . Substituting these values into the equation gives us:

$m = \frac{6\pi - 5\pi}{11\pi - 2\pi} = \frac{\pi}{9\pi} = \frac{1}{9}$

Compare your answer with the correct one above

Question

Figure NOT drawn to scale

On the coordinate axes shown above, the shaded triangle has area 16.

Give the slope of the line that includes the hypotenuse of the triangle.

Answer

The length of the horizontal leg of the triangle is the distance from the origin to , which is 4.

The area of a right triangle is half the product of the lengths of its legs and , so, setting and and solving for :

$\frac{1}{2} ab = A$

$\frac{1}{2} \cdot 4 \cdot b = 16$

$\frac{2b }{2}= \frac{16}{2}$

Since this is the vertical distance from the origin, this is also the absolute value of the -coordinate of the -intercept of the line; also, this point is along the positive -axis. The line has -intercept .

The slope of a line, given the intercepts , is

$m = - \frac{b}{a}$ ,

Substitute and :

$m = - \frac{8}{4} = -2$ .

Compare your answer with the correct one above

Tap the card to reveal the answer

How to find slope of a line - SAT Math

What is a possible slope of line y?

The slope is negative as it starts in quadrant 2 and ends in quadrant 4. Slope is equivlent to the change in y divided by the change in x. The change in y is greater than the change in x, which implies that the slope must be less than –1, leaving –2 as the only possible solution.

What is the slope of a line that runs through points: (-2, 5) and (1, 7)?

The slope of a line is defined as a change in the y coordinates over a change in the x coordinates (rise over run). To calculate the slope of a line, use the following formula:

Find the slope of the line 6X – 2Y = 14

Put the equation in slope-intercept form: y = mx + b -2y = -6x +14 y = 3x – 7 The slope of the line is represented by M; therefore the slope of the line is 3.

A line passes through the points (–3, 5) and (2, 3). What is the slope of this line?

The slope of the line that passes these two points are simply ∆y/∆x = (3-5)/(2+3) = -2/5

What is the slope of line 3 = 8y - 4x?

Solve equation for y. y=mx+b, where m is the slope

Based on the table below, when x = 5, y will equal xy-13011-12-3

What is the slope of the given linear equation? 2x + 4y = -7

We can convert the given equation into slope-intercept form, y=mx+b, where m is the slope. We get y = (-1/2)x + (-7/2)

What is the slope of the line:

First put the question in slope intercept form (y = mx + b): –(1/6)y = –(14/3)x – 7 => y = 6(14/3)x – 7 y = 28x – 7. The slope is 28.

If 2x – 4y = 10, what is the slope of the line?

First put the equation into slope-intercept form, solving for y: 2x – 4y = 10 → –4y = –2x + 10 → y = 1/2*x – 5/2. So the slope is 1/2.

Which of the following lines intersects the y-axis at a thirty degree angle?

What is the slope of the line with equation 4_x_ – 16_y_ = 24?

The equation of a line is: y = mx + b, where m is the slope 4_x_ – 16_y_ = 24 –16_y_ = –4_x_ + 24 y = (–4_x_)/(–16) + 24/(–16) y = (1/4)x – 1.5 Slope = 1/4

What is the slope of a line which passes through coordinates and ?

Slope is found by dividing the difference in the -coordinates by the difference in the -coordinates.

What is the slope of a line that passes though the coordinates and ?

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates. Use the give points in this formula to calculate the slope.

What is the slope of the line represented by the equation ?

What is the slope between and ?

Let and so the slope becomes .

What is the slope of a line running through points and ?

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates. Use the give points in this formula to calculate the slope.

Solve each problem and decide which is the best of the choices given. Find the slope of the line for the given equation.

For this problem, you have to solve for . We want to get the equation in slope-intercept form, where represents the slope of the line. First subtract from each side to get . Then divide both sides by to get . The slope is the number in front of , so the slope is .

Point is at and point is at . What is the slope of the line that connects the two points?

The purpose of this question is to understand how the slope of a line is calculated. The slope is the rise over the run, meaning the change in the y values over the change in the x values . So, the difference in y values divided by the difference in x values yields .

The following two points are located on the same line. What is the slope of the line?

The slope of a line with two points and is given by the following equation: Let and . Substituting these values into the equation gives us:

Figure NOT drawn to scale On the coordinate axes shown above, the shaded triangle has area 16. Give the slope of the line that includes the hypotenuse of the triangle.

The slope of a line is defined as a change in the y coordinates over a change in the x coordinates (rise over run).

To calculate the slope of a line, use the following formula:

Put the equation in slope-intercept form:

y = mx + b

-2y = -6x +14

y = 3x – 7

The slope of the line is represented by M; therefore the slope of the line is 3.

Based on the table below, when x = 5, y will equal

x y
-1 3
0 1
1 -1
2 -3

What is the slope of the given linear equation?

2x + 4y = -7

What is the slope of the line:

$\frac{14}{3}x=\frac{1}{6}y-7$

First put the question in slope intercept form (y = mx + b):

–(1/6)y = –(14/3)x – 7 =>

y = 6(14/3)x – 7

y = 28x – 7.

The slope is 28.

The equation of a line is:

y = mx + b, where m is the slope

4_x_ – 16_y_ = 24

–16_y_ = –4_x_ + 24

y = (–4_x_)/(–16) + 24/(–16)

y = (1/4)x – 1.5

Slope = 1/4

What is the slope of a line which passes through coordinates $\dpi{100} \small (3,7)$ and $\dpi{100} \small (4,12)$ ?

Slope is found by dividing the difference in the $\dpi{100} \small y$ -coordinates by the difference in the $\dpi{100} \small x$ -coordinates.

$\dpi{100} \small \frac{(12-7)}{(4-3)}=\frac{5}{1}=5$

What is the slope of a line that passes though the coordinates $(5,2)$ and $(3,1)$ ?

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{1-2}{3-5}=\frac{-1}{-2}=\frac{1}{2}$

What is the slope of the line represented by the equation $6y-16x=7$ ?

Let $P_{1}=(8,3)$ and $P_{2}=(5,7)$

$m = (y_{2} - y_{1}) \div (x_{2} - x_{1})$ so the slope becomes $-\frac{4}{3}$ .

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{3-(-4)}{7-8}=\frac{7}{-1}=-7$

Solve each problem and decide which is the best of the choices given.

Find the slope of the line for the given equation.

For this problem, you have to solve for . We want to get the equation in slope-intercept form,

where represents the slope of the line.

First subtract from each side to get

.

Then divide both sides by to get

.

The slope is the number in front of , so the slope is .

The following two points are located on the same line. What is the slope of the line?

$(2\pi, 5\pi), (11\pi, 6\pi)$

Figure NOT drawn to scale

On the coordinate axes shown above, the shaded triangle has area 16.

Give the slope of the line that includes the hypotenuse of the triangle.