Plane Geometry - SAT Math
Card 0 of 20
Compare your answer with the correct one above
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
The sum of the interior angles of a polygon is given by 
where 
= number of sides of the polygon. An octagon has 8 sides, so the formula becomes 
The sum of the interior angles of a polygon is given by
Compare your answer with the correct one above
Find the sum of all the inner angles in a hexagon.
Find the sum of all the inner angles in a hexagon.
To solve, simply use the formula to find the total degrees inside a polygon, where n is the number of vertices.
In this particular case, a hexagon means a shape with six sides and thus six vertices.
Thus,
To solve, simply use the formula to find the total degrees inside a polygon, where n is the number of vertices.
In this particular case, a hexagon means a shape with six sides and thus six vertices.
Thus,
Compare your answer with the correct one above
Find the sum of all the angles in a pentagon.
Find the sum of all the angles in a pentagon.
To solve, simply use the formula to find the total degrees in a polygon, where n is thenumber of vertices.
In this particular case, a pentagon is a shape that has five sides and thus has five vertices.
Thus,
To solve, simply use the formula to find the total degrees in a polygon, where n is thenumber of vertices.
In this particular case, a pentagon is a shape that has five sides and thus has five vertices.
Thus,
Compare your answer with the correct one above
If angle A and angle C are complementary angles and B and D are supplementary angles, which of the following must be true?
If angle A and angle C are complementary angles and B and D are supplementary angles, which of the following must be true?
This question is very misleading, because while each answer COULD be true, none of them MUST be true. Between angle A and C, onne of the angles could be very small (0.001 degrees) and the other one could be very large. For instance, if A = 89.9999 and C = 0.0001, AC = 0.009. On the other hand, the two angles could be very siimilar. If B = 90 and D = 90 then BD = 8100 and BD > AC. If we use these same values we disprove AD = BC as 8100 ≠ .009. Finally, if B is a very small value, then B/C will be very small and smaller than A/D.
This question is very misleading, because while each answer COULD be true, none of them MUST be true. Between angle A and C, onne of the angles could be very small (0.001 degrees) and the other one could be very large. For instance, if A = 89.9999 and C = 0.0001, AC = 0.009. On the other hand, the two angles could be very siimilar. If B = 90 and D = 90 then BD = 8100 and BD > AC. If we use these same values we disprove AD = BC as 8100 ≠ .009. Finally, if B is a very small value, then B/C will be very small and smaller than A/D.
Compare your answer with the correct one above
In isosceles triangle ABC, the measure of angle A is 50 degrees. Which is NOT a possible measure for angle B?
In isosceles triangle ABC, the measure of angle A is 50 degrees. Which is NOT a possible measure for angle B?
If angle A is one of the base angles, then the other base angle must measure 50 degrees. Since 50 + 50 + x = 180 means x = 80, the vertex angle must measure 80 degrees.
If angle A is the vertex angle, the two base angles must be equal. Since 50 + x + x = 180 means x = 65, the two base angles must measure 65 degrees.
The only number given that is not possible is 95 degrees.
If angle A is one of the base angles, then the other base angle must measure 50 degrees. Since 50 + 50 + x = 180 means x = 80, the vertex angle must measure 80 degrees.
If angle A is the vertex angle, the two base angles must be equal. Since 50 + x + x = 180 means x = 65, the two base angles must measure 65 degrees.
The only number given that is not possible is 95 degrees.
Compare your answer with the correct one above
In triangle ABC, the measure of angle A = 70 degrees, the measure of angle B = x degrees, and the measure of angle C = y degrees. What is the value of y in terms of x?
In triangle ABC, the measure of angle A = 70 degrees, the measure of angle B = x degrees, and the measure of angle C = y degrees. What is the value of y in terms of x?
Since the three angles of a triangle sum to 180, we know that 70 + x + y = 180. Subtract 70 from both sides and see that x + y = 110. Subtract x from both sides and see that y = 110 – x.
Since the three angles of a triangle sum to 180, we know that 70 + x + y = 180. Subtract 70 from both sides and see that x + y = 110. Subtract x from both sides and see that y = 110 – x.
Compare your answer with the correct one above
What is the measure, in degrees, of each interior angle of a regular convex polygon that has twelve sides?
What is the measure, in degrees, of each interior angle of a regular convex polygon that has twelve sides?
The sum of the interior angles, in degrees, of a regular polygon is given by the formula 180(n – 2), where n is the number of sides. The problem concerns a polygon with twelve sides, so we will let n = 12. The sum of the interior angles in this polygon would be 180(12 – 2) = 180(10) = 1800.
Because the polygon is regular (meaning its sides are all congruent), all of the angles have the same measure. Thus, if we divide the sum of the measures of the angles by the number of sides, we will have the measure of each interior angle. In short, we need to divide 1800 by 12, which gives us 150.
The answer is 150.
The sum of the interior angles, in degrees, of a regular polygon is given by the formula 180(n – 2), where n is the number of sides. The problem concerns a polygon with twelve sides, so we will let n = 12. The sum of the interior angles in this polygon would be 180(12 – 2) = 180(10) = 1800.
Because the polygon is regular (meaning its sides are all congruent), all of the angles have the same measure. Thus, if we divide the sum of the measures of the angles by the number of sides, we will have the measure of each interior angle. In short, we need to divide 1800 by 12, which gives us 150.
The answer is 150.
Compare your answer with the correct one above
A regular polygon has a measure of 
for each of its internal angles. How many sides does it have?
A regular polygon has a measure of 
To determine the measure of the angles of a regular polygon use:
Angle = (n – 2) x 180° / n
Thus, (n – 2) x 180° / n = 140°
180° n - 360° = 140° n
40° n = 360°
n = 360° / 40° = 9
To determine the measure of the angles of a regular polygon use:
Angle = (n – 2) x 180° / n
Thus, (n – 2) x 180° / n = 140°
180° n - 360° = 140° n
40° n = 360°
n = 360° / 40° = 9
Compare your answer with the correct one above
A regular seven sided polygon has a side length of 14”. What is the measurement of one of the interior angles of the polygon?
A regular seven sided polygon has a side length of 14”. What is the measurement of one of the interior angles of the polygon?
The formula for of interior angles based on a polygon with a number of side n is:
Each Interior Angle = (n-2)*180/n
= (7-2)*180/7 = 128.57 degrees
The formula for of interior angles based on a polygon with a number of side n is:
Each Interior Angle = (n-2)*180/n
= (7-2)*180/7 = 128.57 degrees
Compare your answer with the correct one above
In the figure above, polygon ABDFHGEC is a regular octagon. What is the measure, in degrees, of angle FHI?
In the figure above, polygon ABDFHGEC is a regular octagon. What is the measure, in degrees, of angle FHI?
Angle FHI is the supplement of angle FHG, which is an interior angle in the octagon. When two angles are supplementary, their sum is equal to 180 degrees. If we can find the measure of each interior angle in the octagon, then we can find the supplement of angle FHG, which will give us the measure of angle FHI.
The sum of the interior angles in a regular polygon is given by the formula 180(n – 2), where n is the number of sides in the polygon. An octagon has eight sides, so the sum of the angles of the octagon is 180(8 – 2) = 180(6) = 1080 degrees. Because the octagon is regular, all of its sides and angles are congruent. Thus, the measure of each angle is equal to the sum of its angles divided by 8. Therefore, each angle in the polygon has a measure of 1080/8 = 135 degrees. This means that angle FHG has a measure of 135 degrees.
Now that we know the measure of angle FHG, we can find the measure of FHI. The sum of the measures of FHG and FHI must be 180 degrees, because the two angles form a line and are supplementary. We can write the following equation:
Measure of FHG + measure of FHI = 180
135 + measure of FHI = 180
Subtract 135 from both sides.
Measure of FHI = 45 degrees.
The answer is 45.
Angle FHI is the supplement of angle FHG, which is an interior angle in the octagon. When two angles are supplementary, their sum is equal to 180 degrees. If we can find the measure of each interior angle in the octagon, then we can find the supplement of angle FHG, which will give us the measure of angle FHI.
The sum of the interior angles in a regular polygon is given by the formula 180(n – 2), where n is the number of sides in the polygon. An octagon has eight sides, so the sum of the angles of the octagon is 180(8 – 2) = 180(6) = 1080 degrees. Because the octagon is regular, all of its sides and angles are congruent. Thus, the measure of each angle is equal to the sum of its angles divided by 8. Therefore, each angle in the polygon has a measure of 1080/8 = 135 degrees. This means that angle FHG has a measure of 135 degrees.
Now that we know the measure of angle FHG, we can find the measure of FHI. The sum of the measures of FHG and FHI must be 180 degrees, because the two angles form a line and are supplementary. We can write the following equation:
Measure of FHG + measure of FHI = 180
135 + measure of FHI = 180
Subtract 135 from both sides.
Measure of FHI = 45 degrees.
The answer is 45.
Compare your answer with the correct one above
What is the measure of each angle in a regular octagon?
What is the measure of each angle in a regular octagon?
An octagon contains six triangles, or 1080 degrees. This means with 8 angles, each angle is 135 degrees.
An octagon contains six triangles, or 1080 degrees. This means with 8 angles, each angle is 135 degrees.
Compare your answer with the correct one above
What is the measure of each central angle of an octagon?
What is the measure of each central angle of an octagon?
There are 360 degrees and 8 angles, so dividing leaves 45 degrees per angle.
There are 360 degrees and 8 angles, so dividing leaves 45 degrees per angle.
Compare your answer with the correct one above
What is the average (arithmetic mean) of all 15 interior angles of a quadrilateral, pentagon, and hexagon?
What is the average (arithmetic mean) of all 15 interior angles of a quadrilateral, pentagon, and hexagon?
The 4 angles of a quadrilateral add to 360
The 5 angles of a pentagon add to 540
The 6 angles of a hexagon add to 720
The 4 angles of a quadrilateral add to 360
The 5 angles of a pentagon add to 540
The 6 angles of a hexagon add to 720
Compare your answer with the correct one above
Find the sum of the interior angles in a nonagon.
Find the sum of the interior angles in a nonagon.
To solve, simply use the formula for the total degrees in a polygon, where n is the number of vertices.
In this particular case, a nonagon is a shape with nine sides and thus nine vertices.
Thus,
To solve, simply use the formula for the total degrees in a polygon, where n is the number of vertices.
In this particular case, a nonagon is a shape with nine sides and thus nine vertices.
Thus,
Compare your answer with the correct one above
Which of the following cannot be the measure of an exterior angle of a regular polygon?
Which of the following cannot be the measure of an exterior angle of a regular polygon?
If one exterior angle is taken at each vertex of any convex polygon, the sum of their measures is 
. In a regular polygon - one with congruent sides and congruent interior angles, each exterior angle is congruent to one another. If the polygon has 
sides, each exterior angle has measure 
.
Given the common measure 
,
Multiplying both sides by 
:
and
Since 
is equal to a number of sides, it is a whole number. Thus, we are looking for a value of 
which, when we divide 360 by it, yields a non-whole result. We see that 
is the correct choice, since'
A quick check confirms that 360 divided by 8, 10, 12, or 15 yields a whole result.
If one exterior angle is taken at each vertex of any convex polygon, the sum of their measures is
Given the common measure
Multiplying both sides by
and
Since
A quick check confirms that 360 divided by 8, 10, 12, or 15 yields a whole result.
Compare your answer with the correct one above
To the nearest whole degree, give the measure of each interior angle of a regular polygon with 17 sides.
To the nearest whole degree, give the measure of each interior angle of a regular polygon with 17 sides.
The measure of each interior angle of an 
-sided polygon can be calculated using the formula
Setting 
:
The correct choice is therefore 
.
The measure of each interior angle of an
Setting
The correct choice is therefore
Compare your answer with the correct one above
Each interior angle of a regular polygon has measure 
. How many sides does the polygon have?
Each interior angle of a regular polygon has measure
The easiest way to work this is arguably to examine the exterior angles, each of which forms a linear pair with an interior angle. If an interior angle measures 
, then each exterior angle, which is supplementary to an interior angle, measures
The measures of the exterior angles of a polygon, one per vertex, total 
; in a regular polygon, they are congruent, so if there are 
such angles, each measures 
. Since the number of vertices is equal to the number of sides, if we set this equal to 
and solve for 
, we will find the number of sides.
Multiply both sides by 
:
The polygon has 72 vertices and, thus, 72 sides.
The easiest way to work this is arguably to examine the exterior angles, each of which forms a linear pair with an interior angle. If an interior angle measures
The measures of the exterior angles of a polygon, one per vertex, total
Multiply both sides by
The polygon has 72 vertices and, thus, 72 sides.
Compare your answer with the correct one above
If a polygon has 10 sides, what is the measure of each exterior angle?
If a polygon has 10 sides, what is the measure of each exterior angle?
In order to figure this out, we need to remember the formula for finding exterior angles. 
, where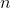 
is the number of sides of a polygon. Now we simply do the following calculation.
So the measure of each exterior angle is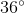 
.
In order to figure this out, we need to remember the formula for finding exterior angles.
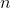
So the measure of each exterior angle is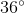
Compare your answer with the correct one above
Acute angles x and y are inside a right triangle. If x is four less than one third of 21, what is y?
Acute angles x and y are inside a right triangle. If x is four less than one third of 21, what is y?
We know that the sum of all the angles must be 180 and we already know one angle is 90, leaving the sum of x and y to be 90.
Solve for x to find y.
One third of 21 is 7. Four less than 7 is 3. So if angle x is 3 then that leaves 87 for angle y.
We know that the sum of all the angles must be 180 and we already know one angle is 90, leaving the sum of x and y to be 90.
Solve for x to find y.
One third of 21 is 7. Four less than 7 is 3. So if angle x is 3 then that leaves 87 for angle y.
Compare your answer with the correct one above