Basic Squaring / Square Roots - SAT Math
Card 0 of 15
Find the square root of the following decimal:

Find the square root of the following decimal:
The easiest way to find the square root of a fraction is to convert it into scientific notation.

The key is that the exponent in scientific notation has to be even for a square root because the square root of an exponent is diving it by two. The square root of 9 is 3, so the square root of 8.1 is a little bit less than 3, around 2.8

The easiest way to find the square root of a fraction is to convert it into scientific notation.
The key is that the exponent in scientific notation has to be even for a square root because the square root of an exponent is diving it by two. The square root of 9 is 3, so the square root of 8.1 is a little bit less than 3, around 2.8
Compare your answer with the correct one above
Find the square root of the following decimal:

Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.

Because  has an even exponent, we can divide the exponenet by 2 to get its square root.
has an even exponent, we can divide the exponenet by 2 to get its square root.

To find the square root of this decimal we convert it into scientific notation.
Because 
Compare your answer with the correct one above
Find the square root of the following decimal:

Find the square root of the following decimal:
This problem can be solve more easily by rewriting the decimal into scientific notation.

Because  has an even exponent, we can take the square root of it by dividing it by 2. The square root of 4 is 2, and the square root of 1 is 1, so the square root of 2.5 is less than 2 and greater than 1.
has an even exponent, we can take the square root of it by dividing it by 2. The square root of 4 is 2, and the square root of 1 is 1, so the square root of 2.5 is less than 2 and greater than 1.

This problem can be solve more easily by rewriting the decimal into scientific notation.
Because 
Compare your answer with the correct one above
Find the square root of the following decimal:

Find the square root of the following decimal:
This problem becomes much simpler if we rewrite the decimal in scientific notation

Because  has an even exponent, we can take its square root by dividing it by two. The square root of 4 is 2, and because 3.6 is a little smaller than 4, its square root is a little smaller than 2, around 1.9
has an even exponent, we can take its square root by dividing it by two. The square root of 4 is 2, and because 3.6 is a little smaller than 4, its square root is a little smaller than 2, around 1.9

This problem becomes much simpler if we rewrite the decimal in scientific notation
Because 
Compare your answer with the correct one above
Find the square root of the following decimal:

Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.

Because  has an even exponent, we can divide the exponenet by 2 to get its square root.
has an even exponent, we can divide the exponenet by 2 to get its square root.  is a perfect square, whose square root is
is a perfect square, whose square root is  .
.

To find the square root of this decimal we convert it into scientific notation.
Because 


Compare your answer with the correct one above
Find the square root of the following decimal:

Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.

Because  has an even exponent, we can divide the exponenet by 2 to get its square root.
has an even exponent, we can divide the exponenet by 2 to get its square root.  is a perfect square, whose square root is
is a perfect square, whose square root is  .
.

To find the square root of this decimal we convert it into scientific notation.
Because 


Compare your answer with the correct one above
Find the square root of the following decimal:

Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.

Because  has an even exponent, we can divide the exponenet by 2 to get its square root. The square root of 9 is 3, and the square root of 4 is two, so the square root of 6.4 is between 3 and 2, around 2.53
has an even exponent, we can divide the exponenet by 2 to get its square root. The square root of 9 is 3, and the square root of 4 is two, so the square root of 6.4 is between 3 and 2, around 2.53

To find the square root of this decimal we convert it into scientific notation.
Because 
Compare your answer with the correct one above
Find the square root of the following decimal:

Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.

Because  has an even exponent, we can divide the exponenet by 2 to get its square root. The square root of 9 is 3, so the square root of 10 should be a little larger than 3, around 3.16
has an even exponent, we can divide the exponenet by 2 to get its square root. The square root of 9 is 3, so the square root of 10 should be a little larger than 3, around 3.16

To find the square root of this decimal we convert it into scientific notation.
Because 
Compare your answer with the correct one above
Find the square root of the following decimal:

Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.

Because  has an even exponent, we can divide the exponenet by 2 to get its square root. The square root of 36 is 6, so the square root of 40 should be a little more than 6, around 6.32.
has an even exponent, we can divide the exponenet by 2 to get its square root. The square root of 36 is 6, so the square root of 40 should be a little more than 6, around 6.32.

To find the square root of this decimal we convert it into scientific notation.
Because 
Compare your answer with the correct one above
Solve for  :
:

Solve for 
Just like any other equation, isolate your variable. Start by multiplying both sides by  :
:

Now, this is the same as:

You know that  is
is  . You can intelligently rewrite this problem as:
. You can intelligently rewrite this problem as:
 , which is the same as:
, which is the same as:

Just like any other equation, isolate your variable. Start by multiplying both sides by 
Now, this is the same as:
You know that 


Compare your answer with the correct one above
Evaluate: 
Evaluate:
The square root of a number returns a positive and negative number that multiplies by itself to obtain the number inside the square root.

The square root of a number returns a positive and negative number that multiplies by itself to obtain the number inside the square root.
Compare your answer with the correct one above
Without using a calculator, solve for x:

Without using a calculator, solve for x:
Simplifying the given equation gives us


Therefore, the correct answer is  .
.
Simplifying the given equation gives us
Therefore, the correct answer is 
Compare your answer with the correct one above
If  and
and  , what is the value of
, what is the value of  ?
?
If 


We are given the equation  . To determine the value of
. To determine the value of  , take the square root of both sides.
, take the square root of both sides.
 .
.
To calculate this value, take note of the following pattern:



Each succeeding radicand is  of the previous radicand, and the value of each succeeding square root is
of the previous radicand, and the value of each succeeding square root is  of the previous value. Continuing the pattern:
of the previous value. Continuing the pattern:
 . However, we are also given the condition that
. However, we are also given the condition that  ; hence, we eliminate the extraneous solution
; hence, we eliminate the extraneous solution  and conclude that the only valid solution of
and conclude that the only valid solution of  is
is  .
.
We are given the equation 


To calculate this value, take note of the following pattern:
Each succeeding radicand is 






Compare your answer with the correct one above
Evaluate:
0.082
Evaluate:
0.082
0.08 * 0.08
First square 8:
8 * 8 = 64
Then move the decimal four places to the left:
0.0064
0.08 * 0.08
First square 8:
8 * 8 = 64
Then move the decimal four places to the left:
0.0064
Compare your answer with the correct one above
If all real values of 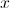 lie between 0 and 1, which of the following is always greater than 1?
lie between 0 and 1, which of the following is always greater than 1?
If all real values of 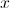
If 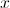 is greater than 0, then adding 1 to
is greater than 0, then adding 1 to  will make it greater than 1. Taking a number between 0 and 1 to a power results in a smaller number.
will make it greater than 1. Taking a number between 0 and 1 to a power results in a smaller number.
If 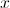

Compare your answer with the correct one above