Graphing - SAT Math

Card 0 of 20

Question

The figure above shows the graph of y = f(x). Which of the following is the graph of y = |f(x)|?

Answer

One of the properties of taking an absolute value of a function is that the values are all made positive. The values themselves do not change; only their signs do. In this graph, none of the y-values are negative, so none of them would change. Thus the two graphs should be identical.

Compare your answer with the correct one above

Question

Below is the graph of the function :

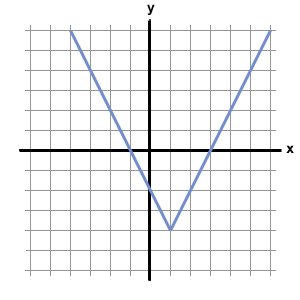
Which of the following could be the equation for ?

Answer

First, because the graph consists of pieces that are straight lines, the function must include an absolute value, whose functions usually have a distinctive "V" shape. Thus, we can eliminate f(x) = x2 – 4x + 3 from our choices. Furthermore, functions with x2 terms are curved parabolas, and do not have straight line segments. This means that f(x) = |x2 – 4x| – 3 is not the correct choice.

Next, let's examine f(x) = |2x – 6|. Because this function consists of an abolute value by itself, its graph will not have any negative values. An absolute value by itself will only yield non-negative numbers. Therefore, because the graph dips below the x-axis (which means f(x) has negative values), f(x) = |2x – 6| cannot be the correct answer.

Next, we can analyze f(x) = |x – 1| – 2. Let's allow x to equal 1 and see what value we would obtain from f(1).

f(1) = | 1 – 1 | – 2 = 0 – 2 = –2

However, the graph above shows that f(1) = –4. As a result, f(x) = |x – 1| – 2 cannot be the correct equation for the function.

By process of elimination, the answer must be f(x) = |2x – 2| – 4. We can verify this by plugging in several values of x into this equation. For example f(1) = |2 – 2| – 4 = –4, which corresponds to the point (1, –4) on the graph above. Likewise, if we plug 3 or –1 into the equation f(x) = |2x – 2| – 4, we obtain zero, meaning that the graph should cross the x-axis at 3 and –1. According to the graph above, this is exactly what happens.

The answer is f(x) = |2x – 2| – 4.

Compare your answer with the correct one above

Question

Which of the following could be a value of $f(x)$ for $f(x)=-x^2 + 3$ ?

Answer

The graph is a down-opening parabola with a maximum of $y=3$ . Therefore, there are no y values greater than this for this function.

Compare your answer with the correct one above

Question

What is the equation for the line pictured above?

Answer

A line has the equation

where is the intercept and is the slope.

The intercept can be found by noting the point where the line and the y-axis cross, in this case, at so .

The slope can be found by selecting two points, for example, the y-intercept and the next point over that crosses an even point, for example, .

Now applying the slope formula,

$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

which yields $m=\frac{-1-2}{2-0}=-\frac{3}{2}$ .

Therefore the equation of the line becomes:

$y=-\frac{3}{2}x+2$

Compare your answer with the correct one above

Question

Which of the following graphs represents the y-intercept of this function?

Answer

Graphically, the y-intercept is the point at which the graph touches the y-axis. Algebraically, it is the value of when .

Here, we are given the function . In order to calculate the y-intercept, set equal to zero and solve for .

So the y-intercept is at .

Compare your answer with the correct one above

Question

Which of the following graphs represents the x-intercept of this function?

Answer

Graphically, the x-intercept is the point at which the graph touches the x-axis. Algebraically, it is the value of for which .

Here, we are given the function . In order to calculate the x-intercept, set equal to zero and solve for .

So the x-intercept is at .

Compare your answer with the correct one above

Question

Which of the following represents $f(x)=\frac{1}{2}x-2$ ?

Answer

A line is defined by any two points on the line. It is frequently simplest to calculate two points by substituting zero for x and solving for y, and by substituting zero for y and solving for x.

$f(x)=\frac{1}{2}x-2$

Let . Then

$y=\frac{1}{2}(0)-2$

So our first set of points (which is also the y-intercept) is

Let . Then

$0=\frac{1}{2}x-2$

$2=\frac{1}{2}x$

So our second set of points (which is also the x-intercept) is .

Compare your answer with the correct one above

Question

The graphic shows Bob's walk. At what times is Bob the furthest from home?

Answer

If we look at the graph, the line segment from to , is the furthest from home. So the answer will be from $\text{Time}=8$ to $\text{Time}=14$ .

Compare your answer with the correct one above

Question

The equation represents a line. This line does NOT pass through which of the four quadrants?

Answer

Plug in for to find a point on the line:

Thus, is a point on the line.

Plug in for to find a second point on the line:

is another point on the line.

Now we know that the line passes through the points and .

A quick sketch of the two points reveals that the line passes through all but the third quadrant.

Compare your answer with the correct one above

Question

A line graphed on the coordinate plane below.

Give the equation of the line in slope intercept form.

Answer

The slope of the line is $\dpi{100} \small -2$ and the y-intercept is $\dpi{100} \small 4$ .

The equation of the line is $\dpi{100} \small y=-2x+4$ .

Compare your answer with the correct one above

Question

Give the equation of the curve.

Answer

This is the parent graph of $\dpi{100} \small x^{3}$ . Since the graph in question is negative, then we flip the quadrants in which it will approach infinity. So the graph of $\dpi{100} \small y=-x^{3}$ will start in quadrant 2 and end in 4.

Compare your answer with the correct one above

Question

Billy set up a ramp for his toy cars. He did this by taking a wooden plank and putting one end on top of a brick that was 3 inches high. He then put the other end on top of a box that was 9 inches high. The bricks were 18 inches apart. What is the slope of the plank?

Answer

The value of the slope (m) is rise over run, and can be calculated with the formula below:

$m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

The coordinates of the first end of the plank would be (0,3), given that this is the starting point of the plank (so x would be 0), and y would be 3 since the brick is 3 inches tall.

The coordinates of the second end of the plank would be (18,9) since the plank is 18 inches long (so x would be 18) and y would be 9 since the box was 9 inches tall at the other end.

From this information we know that we can assign the following coordinates for the equation:

$\left(x_{1},y_{1}\right) = (0,3)$ and $(x_{2}, y_{2})= (18,9)$

Below is the solution we would get from plugging this information into the equation for slope:

$m = \frac{9-3}{18-0}}$

This reduces to $\frac{6}{18} =\frac{1}{3}$

Compare your answer with the correct one above

Question

What is the slope of the line depicted by the graph?

Answer

Looking at the graph, it is seen that the line passes through the points (-8,-5) and (8,5).

The slope of a line through the points and can be found by setting

$x_{1} = -8,y_{1} = -5, x_{2} = 8, y_{2} = 5$ :

in the slope formula:

$m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{5-(-5)}{8 - (-8)} = \frac{5+5}{8 + 8} = \frac{10}{16} = \frac{5}{8}$

Compare your answer with the correct one above

Question

Give the area of the triangle on the coordinate plane that is bounded by the lines of the equations , and .

Answer

It is necessary to find the coordinates of the vertices of the triangle, each of which is the intersection of two of the three lines.

The intersection of the lines of the equations and can be found by noting that, by substituting for in the latter equation, , making the point of intersection .

The intersection of the lines of the equations and can be found by substituting for in the latter equation and solving for :

$\frac{4x}{4} = \frac{5}{4}$

$x = 1 \frac{1}{4}$

This point of intersection is $\left ( 1 \frac{1}{4}, -2 \right )$ .

The intersection of the lines of the equations and can be found by substituting for in the latter equation and solving for :

$\frac{3x }{3}= \frac{7}{3}$

$x = 2\frac{1}{3}$

Since , $y = 2\frac{1}{3}$ , and this point of intersection is $\left ( 2\frac{1}{3}, 2\frac{1}{3} \right )$ .

The lines in question are graphed below, and the triangle they bound is shaded:

We can take the horizontal side as the base of the triangle; its length is the difference of the -coordinates:

$b = 1\frac{1}{4} - (-2 ) = 3 \frac{1}{4}$

The height is the vertical distance from this side to the opposite side, which is the difference of the -coordinates:

$h = 2 \frac{1}{3} - (-2) = 4 \frac{1}{3}$

The area is half their product:

$A = \frac{1}{2} bh = \frac{1}{2} \cdot 3 \frac{1}{4} \cdot 4 \frac{1}{3} =7 \frac{1}{24}$

Compare your answer with the correct one above

Question

What is the -intercept of the function that is depicted in the graph above?

Answer

This question tests one's ability to recognize algebraic characteristics of a graph. This particular question examines a linear function.

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Step 1: Identify the general algebraic function for the given graph.

Since the graph is that of a straight line, the general algebraic form of the function is,

where

$\m=\textup{slope} \b=\textup{y-intercept}$

Step 2: Identify where the graph crosses the -axis.

Therefore the general form of the function looks like,

Step 3: Answer the question.

The -intercept is three.

Compare your answer with the correct one above

Question

On the coordinate plane, , , and are the points with coordinates , , and , respectively. Lines , , and are the perpendicular bisectors of $\overline{XY}$ , $\overline{XZ}$ , and $\overline{YZ}$ , respectively.

and intersect at a point ; and intersect at a point ; and intersect at a point .

Which of these statements is true of , , and ?

Answer

Another way of viewing this problem is to note that the three given vertices form a triangle $\bigtriangleup XYZ$ whose sides' perpendicular bisectors intersect at the points , , and . However, the three perpendicular bisectors of the sides of any triangle always intersect at a common point. The correct response is that , , and are the same point.

Compare your answer with the correct one above

Question

On the coordinate plane, a triangle has its vertices at the points with coordinates

, , and . Give the coordinates of the center of the circle that circumscribes this triangle.

Answer

The referenced figure is below.

The two non-horizontal line segments are perpendicular, as is proved as follows:

The slope of the line that connects and can be found using the slope formula, setting $x_{1} = 12 , y_{2} = x_{2} = 0, y_{2} = 12$ :

$m_{1} = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}= \frac{12-0}{0-12} = \frac{12}{-12} = -1$

The slope of the line that connects and can be found similarly, setting $x_{1} = 12 , y_{2} = x_{2} = 0, y_{2} = -12$ :

$m_{2} = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}= \frac{-12-0}{0-12} = \frac{-12}{-12} = 1$

The product of their slopes is $m_{1} m_{2} = -1 \cdot 1 = -1$ , which indicates perpendicularity between the sides.

This makes the triangle right, and the side with endpoints and the hypotenuse. The center of the circle that circumscribes a right triangle is the midpoint of its hypotenuse, which is easily be seen to be the origin, .

Compare your answer with the correct one above

Question

On the coordinate plane, a triangle has its vertices at the points with coordinates , , and . Give the coordinates of the center of the circle that circumscribes this triangle.

Answer

The referenced figure is below.

The triangle formed is a right triangle whose hypotenuse is the segment with the endpoints and . The center of the circle that circumscribes a right triangle is the midpoint of its hypotenuse, so the midpoint formula

$(x_{M}, y_{M}) = \left ( \frac{x_{1}+ x_{2} }{2},\frac{y_{1}+ y_{2} }{2} \right )$

can be applied, setting $x_{1} = 12, y_{1} = x_{2} = 0, y_{2} = 8$ :

$x_{M}= \frac{x_{1}+ x_{2} }{2}= \frac{12+0}{2}= \frac{12}{2} = 6$

$y_{M}= \frac{y_{1}+ y_{2} }{2}= \frac{0+8}{2}= \frac{8}{2} = 4$

The midpoint of the hypotenuse, and, consequently, the center of the circumscribed circle, is the point with coordinates .

Compare your answer with the correct one above

Question

Figure NOT drawn to scale.

On the coordinate axes shown above, the shaded triangle has area 40.

Evaluate .

Answer

The length of the horizontal leg of the triangle is the distance from the origin to , which is 8.

The area of a right triangle is half the product of the lengths of its legs and , so, setting and and solving for :

$\frac{1}{2} ab = A$

$\frac{1}{2} \cdot 8 \cdot b = 40$

$\frac{4 b}{4} = \frac{40}{4}$

Therefore, the length of the vertical leg is 10, and, since the -intercept of the line containing the hypotenuse is on the positive -axis, this intercept is . The slope of a line with intercepts is

$m = - \frac{b}{a}$ ,

so, setting and :

$m = - \frac{10}{8} = -\frac{5}{4}$

Set $m = -\frac{5}{4}$ and in the slope-intercept form of the equation of a line,

;

the line has equation

$y = -\frac{5}{4}x+10$

The -coordinate of the point on the line with -coordinate 2 can be found using substitution; setting ::

$Y = -\frac{5}{4} (2)+10 = -\frac{5}{2} + 10 = -2\frac{1}{2} + 10 = 7 \frac{1}{2}$

Compare your answer with the correct one above

Question

Mrs. Smith's 8th grade class has a weekly quiz. The graph below depicts the number of questions students got incorrect on their quiz and their corresponding quiz grade. Examining the graph, what type of correlation if any, exists?

Answer

Mrs. Smith's 8th grade class had a quiz last week. The graph below depicts the number of questions students got incorrect on their quiz and their corresponding quiz grade. In other words, the graph in this particular question is a dot plot and the question asks to find a correlation if one exists.

Recall that a correlation is a trend seen in the data. Graphically, trends can be either:

I. Positive

II. Negative

III. Constant

IV. No trend

For a trend to be positive the x and y variable both increase. A trend is negative when the y variable (dependent variable) decreases as the x variable (independent variable) increases. A constant trend occurs when the y variable stays the same as the x variable increases. No trend exists when the data appears to be scattered with no association between the x and y variables.

Examining the graph given it is seen that the x variable is the number of questions missed and the y variable is the overall score on the quiz. It is seen that as the number of questions missed increases, the overall score on the quiz decreases. This describes a negative trend.

In other words, the graph depicts a negative correlation.

Compare your answer with the correct one above

Tap the card to reveal the answer