Simplifying Square Roots - SAT Math

Card 0 of 20

Question

If m and n are postive integers and 4m = 2n, what is the value of m/n?

Answer

22 = 4. Also, following the rules of exponents, 41 = 1.

One can therefore say that m = 1 and n = 2.

The question asks to solve for m/n. Since m = 1 and n = 2, m/n = 1/2.

Compare your answer with the correct one above

Question

Simplify:

$\sqrt[2]{24,300}$

Answer

$\sqrt[2]{24,300}$

When simplifying the square root of a number that may not have a whole number root, it's helpful to approach the problem by finding common factors of the number inside the radicand. In this case, the number is 24,300.

What are the factors of 24,300?

24,300 can be factored into:

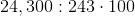
$24,300: 243\cdot 100$

When there are factors that appear twice, they may be pulled out of the radicand. For instance, 100 is a multiple of 24,300. When 100 is further factored, it is $10^{2}$ (or 10x10). However, 100 wouldn't be pulled out of the radicand, but the square root of 100 because the square root of 24,300 is being taken. The 100 is part of the24,300. This means that the problem would be rewritten as: $10\sqrt[2]{243}$

But 243 can also be factored: $24,300: (3\cdot 81)\cdot100$
$24,300: {\color{Orange} 9}\cdot{\color{Orange} 9}\cdot {\color{Cyan} 10}\cdot {\color{cyan} 10}\cdot 3$
Following the same principle as for the 100, the problem would become
$9\cdot 10\sqrt[2]{3}$ because there is only one factor of 3 left in the radicand. If there were another, the radicand would be lost and it would be 9103.
9 and 10 may be multiplied together, yielding the final simplified answer of
$90\sqrt[2]{3}$

Compare your answer with the correct one above

Question

$\sqrt{180} + \sqrt{125} = ?$

Answer

To solve the equation $\sqrt{180} + \sqrt{125} = ?$ , we can first factor the numbers under the square roots.

$\sqrt{2\cdot 2\cdot 3\cdot 3\cdot 5} + \sqrt{5\cdot 5\cdot 5} = ?$

When a factor appears twice, we can take it out of the square root.

$2\cdot 3\sqrt{5} + 5\sqrt{5} = ?$

$6\sqrt{5} + 5\sqrt{5} = ?$

Now the numbers can be added directly because the expressions under the square roots match.

$6\sqrt{5} + 5\sqrt{5} = 11\sqrt{5}$

Compare your answer with the correct one above

Question

what is

√0.0000490

Answer

easiest way to simplify: turn into scientific notation

√0.0000490= √4.9 X 10-5

finding the square root of an even exponent is easy, and 49 is a perfect square, so we can write out an improper scientific notation:

√4.9 X 10-5 = √49 X 10-6

√49 = 7; √10-6 = 10-3 this is equivalent to raising 10-6 to the 1/2 power, in which case all that needs to be done is multiply the two exponents: 7 X 10-3= 0.007

Compare your answer with the correct one above

Question

Simplify:

√112

Answer

√112 = {√2 * √56} = {√2 * √2 * √28} = {2√28} = {2√4 * √7} = 4√7

Compare your answer with the correct one above

Question

Simplify the following: (√(6) + √(3)) / √(3)

Answer

Begin by multiplying top and bottom by √(3):

(√(18) + √(9)) / 3

Note the following:

√(9) = 3

√(18) = √(9 * 2) = √(9) * √(2) = 3 * √(2)

Therefore, the numerator is: 3 * √(2) + 3. Factor out the common 3: 3 * (√(2) + 1)

Rewrite the whole fraction:

(3 * (√(2) + 1)) / 3

Simplfy by dividing cancelling the 3 common to numerator and denominator: √(2) + 1

Compare your answer with the correct one above

Question

Simplify:

√192

Answer

√192 = √2 X √96

√96 = √2 X √48

√48 = √4 X√12

√12 = √4 X √3

√192 = √(2X2X4X4) X √3

= √4X√4X√4 X √3

= 8√3

Compare your answer with the correct one above

Question

Simplify

9 ÷ √3

Answer

in order to simplify a square root on the bottom, multiply top and bottom by the root

Compare your answer with the correct one above

Question

Which of the following is the most simplified form of:

$\sqrt{468}$

Answer

First find all of the prime factors of

$468=6\ast78=6\ast6\ast13=2\ast3\ast2\ast3\ast13$

So $\sqrt{468}=\sqrt{2\ast2\ast3\ast3\ast13}=2\ast3\sqrt{13}=6\sqrt{13}$

Compare your answer with the correct one above

Question

Which of the following is equal to $\sqrt{75}$ ?

Answer

√75 can be broken down to √25 * √3. Which simplifies to 5√3.

Compare your answer with the correct one above

Question

Simplify:

$4\sqrt{27}+16\sqrt{75}+3\sqrt{12}$

Answer

4√27 + 16√75 +3√12 =

4(√3)(√9) + 16(√3)(√25) +3(√3)(√4) =

4(√3)(3) + 16(√3)(5) + 3(√3)(2) =

12√3 + 80√3 +6√3= 98√3

Compare your answer with the correct one above

Question

Simplify: $\sqrt{576}$

Answer

In order to take the square root, divide 576 by 2.

$\dpi{100} \sqrt{576}= \sqrt{2}\sqrt{288}=\sqrt{2}\sqrt{2}\sqrt{144}=\sqrt{4}\sqrt{144}=2\cdot 12=24$

Compare your answer with the correct one above

Question

Simplify $(\frac{16}{81})^{1/4}$ .

Answer

$(\frac{16}{81})^{1/4}$

$\frac{16^{1/4}}{81^{1/4}}$

$\frac{(2\cdot 2\cdot 2\cdot 2)^{1/4}}{(3\cdot 3\cdot 3\cdot 3)^{1/4}}$

$\frac{2}{3}$

Compare your answer with the correct one above

Question

What is the simplest way to express $\sqrt{3888}$ ?

Answer

First we will list the factors of 3888:

$3888=3\times1296=3\times\3\times432=3^2\times12\times36=3^2\times12\times12\times3=3^2\times12^2\times3$

$\sqrt{3888}=\sqrt{3^{2}\times 12^{2}\times 3}=\sqrt{3^{2}}\times\sqrt{12^{2}} \times \sqrt{3}=3\times 12\times \sqrt{3}=36\sqrt{3}$

Compare your answer with the correct one above

Question

Simplify $\sqrt{a^{3}b^{4}c^{5}}$ .

Answer

Rewrite what is under the radical in terms of perfect squares:

$x^{2}=x\cdot x$

$x^{4}=x^{2}\cdot x^{2}$

$x^{6}=x^{3}\cdot x^{3}$

Therefore, $\sqrt{a^{3}b^{4}c^{5}}= \sqrt{a^{2}a^{1}b^{4}c^{4}c^{1}}=ab^{2}c^{2}\sqrt{ac}$ .

Compare your answer with the correct one above

Question

Which of the following is equivalent to $\frac{x + \sqrt{3}}{3x + \sqrt{2}}$ ?

Answer

Multiply by the conjugate and the use the formula for the difference of two squares:

$\frac{x + \sqrt{3}}{3x + \sqrt{2}}$

$\frac{x + \sqrt{3}}{3x + \sqrt{2}}\cdot \frac{3x - \sqrt{2}}{3x - \sqrt{2}}$

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{(3x)^{2} - (\sqrt{2})^{2}}$

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{9x^{2} - 2}$

Compare your answer with the correct one above

Question

What is $\sqrt{50}$ ?

Answer

We know that 25 is a factor of 50. The square root of 25 is 5. That leaves $\sqrt{2}$ which can not be simplified further.

Compare your answer with the correct one above

Question

Simplify:

$\sqrt{48}$

Answer

To simplify, we want to find some factors of where at least one of the factors is a perfect square.

In this case, and are factors of , and is a perfect square.

We can simplify by saying:

$\sqrt{48} = \sqrt{16\cdot 3} = \sqrt{4^2 \cdot 3} = 4\sqrt{3}$

We could also recognize that two factors of are and . We could approach this way by saying:

$\sqrt{48}=\sqrt{4 \cdot 12} = \sqrt {2^2 \cdot 12} = 2\sqrt{12}$

But we wouldn't stop there. That's because can be further factored:

$2\sqrt{12} = 2\sqrt{4 \cdot 3} = 2\sqrt{2^2 \cdot 3} = 2\cdot 2 \sqrt{3} = 4\sqrt{3}$

Compare your answer with the correct one above

Question

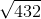
What is $\sqrt{432}$ equal to?

Answer

$\sqrt{432}$

1. We know that , which we can separate under the square root:

$\sqrt{144\cdot 3}$

2. 144 can be taken out since it is a perfect square: $12\cdot12=144$ . This leaves us with:

$12\sqrt{3}$

This cannot be simplified any further.

Compare your answer with the correct one above

Question

Simplfy the following radical $\sqrt{20x^{2}}$ .

Answer

You can rewrite the equation as $\sqrt{20x^2}=(x)\sqrt{5} \cdot \sqrt{4}$ .

This simplifies to $2x\sqrt{5}$ .

Compare your answer with the correct one above

Tap the card to reveal the answer