Variables - SAT Math
Card 0 of 20
Subtract  from
from  .
.
Subtract 

Step 1: We need to read the question carefully. It says subtract from. When you see the word "from", you read the question right to left.
I am subtracting the left equation from the right equation.
Step 2: We need to write the equation on the right minus the equation of the left.

Step 3: Distribute the minus sign in front of the parentheses:

Step 4: Combine like terms:



Step 5: Put all the terms together, starting with highest degree. The degree of the terms is the exponent. Here, the highest degree is 2 and lowest is zero.
The final equation is 
Step 1: We need to read the question carefully. It says subtract from. When you see the word "from", you read the question right to left.
I am subtracting the left equation from the right equation.
Step 2: We need to write the equation on the right minus the equation of the left.
Step 3: Distribute the minus sign in front of the parentheses:
Step 4: Combine like terms:
Step 5: Put all the terms together, starting with highest degree. The degree of the terms is the exponent. Here, the highest degree is 2 and lowest is zero.
The final equation is
Compare your answer with the correct one above
Given a♦b = (a+b)/(a-b) and b♦a = (b+a)/(b-a), which of the following statement(s) is(are) true:
I. a♦b = -(b♦a)
II. (a♦b)(b♦a) = (a♦b)2
III. a♦b + b♦a = 0
Given a♦b = (a+b)/(a-b) and b♦a = (b+a)/(b-a), which of the following statement(s) is(are) true:
I. a♦b = -(b♦a)
II. (a♦b)(b♦a) = (a♦b)2
III. a♦b + b♦a = 0
Notice that - (a-b) = b-a, so statement I & III are true after substituting the expression. Substitute the expression for statement II gives ((a+b)/(a-b))((a+b)/(b-a))=((a+b)(b+a))/((-1)(a-b)(a-b))=-1 〖(a+b)〗2/〖(a-b)〗2 =-((a+b)/(a-b))2 = -(a♦b)2 ≠ (a♦b)2
Notice that - (a-b) = b-a, so statement I & III are true after substituting the expression. Substitute the expression for statement II gives ((a+b)/(a-b))((a+b)/(b-a))=((a+b)(b+a))/((-1)(a-b)(a-b))=-1 〖(a+b)〗2/〖(a-b)〗2 =-((a+b)/(a-b))2 = -(a♦b)2 ≠ (a♦b)2
Compare your answer with the correct one above
If a positive integer a is divided by 7, the remainder is 4. What is the remainder if 3_a_ + 5 is divided by 3?
If a positive integer a is divided by 7, the remainder is 4. What is the remainder if 3_a_ + 5 is divided by 3?
The best way to solve this problem is to plug in an appropriate value for a. For example, plug-in 11 for a because 11 divided by 7 will give us a remainder of 4.
Then 3_a + 5_, where a = 11, gives us 38. Then 38 divided by 3 gives a remainder of 2.
The algebra method is as follows:
a divided by 7 gives us some positive integer b, with a remainder of 4.
Thus,
a / 7 = b 4/7
a / 7 = (7_b +_ 4) / 7
a = (7_b_ + 4)
then 3_a + 5 =_ 3 (7_b_ + 4) + 5
(3_a_+5)/3 = \[3(7_b_ + 4) + 5\] / 3
= (7_b_ + 4) + 5/3
The first half of this expression (7_b_ + 4) is a positive integer, but the second half of this expression (5/3) gives us a remainder of 2.
The best way to solve this problem is to plug in an appropriate value for a. For example, plug-in 11 for a because 11 divided by 7 will give us a remainder of 4.
Then 3_a + 5_, where a = 11, gives us 38. Then 38 divided by 3 gives a remainder of 2.
The algebra method is as follows:
a divided by 7 gives us some positive integer b, with a remainder of 4.
Thus,
a / 7 = b 4/7
a / 7 = (7_b +_ 4) / 7
a = (7_b_ + 4)
then 3_a + 5 =_ 3 (7_b_ + 4) + 5
(3_a_+5)/3 = \[3(7_b_ + 4) + 5\] / 3
= (7_b_ + 4) + 5/3
The first half of this expression (7_b_ + 4) is a positive integer, but the second half of this expression (5/3) gives us a remainder of 2.
Compare your answer with the correct one above
Compare your answer with the correct one above
Simplify: 
Simplify:
Cancel by subtracting the exponents of like terms:

Cancel by subtracting the exponents of like terms:
Compare your answer with the correct one above
If 3 less than 15 is equal to 2x, then 24/x must be greater than
If 3 less than 15 is equal to 2x, then 24/x must be greater than
Set up an equation for the sentence: 15 – 3 = 2x and solve for x. X equals 6. If you plug in 6 for x in the expression 24/x, you get24/6 = 4. 4 is only choice greater than a.
Set up an equation for the sentence: 15 – 3 = 2x and solve for x. X equals 6. If you plug in 6 for x in the expression 24/x, you get24/6 = 4. 4 is only choice greater than a.
Compare your answer with the correct one above
By what expression can  be multiplied to yield the product
be multiplied to yield the product  ?
?
By what expression can 

Divide  by
by  by setting up a long division.
by setting up a long division.
Divide the lead term of the dividend,  , by that of the divisor,
, by that of the divisor,  ; the result is
; the result is 
Enter that as the first term of the quotient. Multiply this by the divisor:

Subtract this from the dividend. This is shown in the figure below.

Repeat the process with the new difference:



Repeating:



The quotient - and the correct response - is  .
.
Divide 

Divide the lead term of the dividend, 

Enter that as the first term of the quotient. Multiply this by the divisor:
Subtract this from the dividend. This is shown in the figure below.

Repeat the process with the new difference:

Repeating:

The quotient - and the correct response - is 
Compare your answer with the correct one above
Divide  by
by  .
.
Divide 

It is not necessary to work a long division if you recognize  as the sum of two perfect cube expressions:
as the sum of two perfect cube expressions:

A sum of cubes can be factored according to the pattern
 ,
,
so, setting  ,
,
![x^{3} + (5y )^{3} =(x+5y) [x ^{2}+ x \cdot 5y + (5y)^{2}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/842425/gif.latex)

Therefore,

It is not necessary to work a long division if you recognize 
A sum of cubes can be factored according to the pattern

so, setting 
Therefore,
Compare your answer with the correct one above
What is a possible value for x in x2 – 12x + 36 = 0 ?
What is a possible value for x in x2 – 12x + 36 = 0 ?
You need to factor to find the possible values for x. You need to fill in the blanks with two numbers with a sum of -12 and a product of 36. In both sets of parenthesis, you know you will be subtracting since a negative times a negative is a positive and a negative plus a negative is a negative
(x –__)(x –__).
You should realize that 6 fits into both blanks.
You must now set each set of parenthesis equal to 0.
x – 6 = 0; x – 6 = 0
Solve both equations: x = 6
You need to factor to find the possible values for x. You need to fill in the blanks with two numbers with a sum of -12 and a product of 36. In both sets of parenthesis, you know you will be subtracting since a negative times a negative is a positive and a negative plus a negative is a negative
(x –__)(x –__).
You should realize that 6 fits into both blanks.
You must now set each set of parenthesis equal to 0.
x – 6 = 0; x – 6 = 0
Solve both equations: x = 6
Compare your answer with the correct one above
If r and t are constants and x2 +rx +6=(x+2)(x+t), what is the value of r?
If r and t are constants and x2 +rx +6=(x+2)(x+t), what is the value of r?
We first expand the right hand side as x2+2x+tx+2t and factor out the x terms to get x2+(2+t)x+2t. Next we set this equal to the original left hand side to get x2+rx +6=x2+(2+t)x+2t, and then we subtract x2 from each side to get rx +6=(2+t)x+2t. Since the coefficients of the x terms on each side must be equal, and the constant terms on each side must be equal, we find that r=2+t and 6=2t, so t is equal to 3 and r is equal to 5.
We first expand the right hand side as x2+2x+tx+2t and factor out the x terms to get x2+(2+t)x+2t. Next we set this equal to the original left hand side to get x2+rx +6=x2+(2+t)x+2t, and then we subtract x2 from each side to get rx +6=(2+t)x+2t. Since the coefficients of the x terms on each side must be equal, and the constant terms on each side must be equal, we find that r=2+t and 6=2t, so t is equal to 3 and r is equal to 5.
Compare your answer with the correct one above
2x + 3y = 5a + 2b (1)
3x + 2y = 4a – b (2)
Express x2 – y2 in terms of a and b
2x + 3y = 5a + 2b (1)
3x + 2y = 4a – b (2)
Express x2 – y2 in terms of a and b
Add the two equations together to yield 5x + 5y = 9a + b, then factor out 5 to get 5(x + y) = 9a + b; divide both sides by 5 to get x + y = (9a + b)/5; subtract the two equations to get x - y = -a - 3b. So, x2 – y2 = (x + y)(x – y) = (9a + b)/5 (–a – 3b) = (–\[(9a)\]2 – 28ab – \[(3b)\]2)/5
Add the two equations together to yield 5x + 5y = 9a + b, then factor out 5 to get 5(x + y) = 9a + b; divide both sides by 5 to get x + y = (9a + b)/5; subtract the two equations to get x - y = -a - 3b. So, x2 – y2 = (x + y)(x – y) = (9a + b)/5 (–a – 3b) = (–\[(9a)\]2 – 28ab – \[(3b)\]2)/5
Compare your answer with the correct one above
Let  and
and  be integers, such that
be integers, such that  . If
. If  and
and  , then what is
, then what is  ?
?
Let 





We are told that x3 - y3 = 56. We can factor the left side of the equation using the formula for difference of cubes.
x3 - y3 = (x - y)(x2 + xy + y2) = 56
Since x - y = 2, we can substitute this value in for the factor x - y.
2(x2 + xy + y2) = 56
Divide both sides by 2.
x2 + xy + y2 = 28
Because we are trying to find x2 + y2, if we can get rid of xy, then we would have our answer.
We are told that 3xy = 24. If we divide both sides by 3, we see that xy = 8.
We can then substitute this value into the equation x2 + xy + y2 = 28.
x2 + 8 + y2 = 28
Subtract both sides by eight.
x2 + y2 = 20.
The answer is 20.
ALTERNATE SOLUTION:
We are told that x - y = 2 and 3xy = 24. This is a system of equations.
If we solve the first equation in terms of x, we can then substitute this into the second equation.
x - y = 2
Add y to both sides.
x = y + 2
Now we will substitute this value for x into the second equation.
3(y+2)(y) = 24
Now we can divide both sides by three.
(y+2)(y) = 8
Then we distribute.
y2 + 2y = 8
Subtract 8 from both sides.
y2 + 2y - 8 = 0
We need to factor this by thinking of two numbers that multiply to give -8 but add to give 2. These numbers are 4 and -2.
(y + 4)(y - 2) = 0
This means either y - 4 = 0, or y + 2 = 0
y = -4, or y = 2
Because x = y + 2, if y = -4, then x must be -2. Similarly, if y = 2, then x must be 4.
Let's see which combination of x and y will satisfy the final equation that we haven't used, x3 - y3 = 56.
If x = -2 and y = -4, then
(-2)3 - (-4)3 = -8 - (-64) = 56. So that means that x= -2 and y = -4 is a valid solution.
If x = 4 and y = 2, then
(4)3 - 23 = 64 - 8 = 56. So that means x = 4 and y = 2 is also a valid solution.
The final value we are asked to find is x2 + y2.
If x= -2 and y = -4, then x2 + y2 = (-2)2 + (-4)2 = 4 + 16 = 20.
If x = 4 and y = 2, then x2 + y2 = (4)2 + 22 = 16 + 4 = 20.
Thus, no matter which solution we use for x and y, x2 + y2 = 20.
The answer is 20.
We are told that x3 - y3 = 56. We can factor the left side of the equation using the formula for difference of cubes.
x3 - y3 = (x - y)(x2 + xy + y2) = 56
Since x - y = 2, we can substitute this value in for the factor x - y.
2(x2 + xy + y2) = 56
Divide both sides by 2.
x2 + xy + y2 = 28
Because we are trying to find x2 + y2, if we can get rid of xy, then we would have our answer.
We are told that 3xy = 24. If we divide both sides by 3, we see that xy = 8.
We can then substitute this value into the equation x2 + xy + y2 = 28.
x2 + 8 + y2 = 28
Subtract both sides by eight.
x2 + y2 = 20.
The answer is 20.
ALTERNATE SOLUTION:
We are told that x - y = 2 and 3xy = 24. This is a system of equations.
If we solve the first equation in terms of x, we can then substitute this into the second equation.
x - y = 2
Add y to both sides.
x = y + 2
Now we will substitute this value for x into the second equation.
3(y+2)(y) = 24
Now we can divide both sides by three.
(y+2)(y) = 8
Then we distribute.
y2 + 2y = 8
Subtract 8 from both sides.
y2 + 2y - 8 = 0
We need to factor this by thinking of two numbers that multiply to give -8 but add to give 2. These numbers are 4 and -2.
(y + 4)(y - 2) = 0
This means either y - 4 = 0, or y + 2 = 0
y = -4, or y = 2
Because x = y + 2, if y = -4, then x must be -2. Similarly, if y = 2, then x must be 4.
Let's see which combination of x and y will satisfy the final equation that we haven't used, x3 - y3 = 56.
If x = -2 and y = -4, then
(-2)3 - (-4)3 = -8 - (-64) = 56. So that means that x= -2 and y = -4 is a valid solution.
If x = 4 and y = 2, then
(4)3 - 23 = 64 - 8 = 56. So that means x = 4 and y = 2 is also a valid solution.
The final value we are asked to find is x2 + y2.
If x= -2 and y = -4, then x2 + y2 = (-2)2 + (-4)2 = 4 + 16 = 20.
If x = 4 and y = 2, then x2 + y2 = (4)2 + 22 = 16 + 4 = 20.
Thus, no matter which solution we use for x and y, x2 + y2 = 20.
The answer is 20.
Compare your answer with the correct one above
Solve for  :
:

Solve for 

First, add 4 to both sides:

Divide both sides by 2:


First, add 4 to both sides:
Divide both sides by 2:
Compare your answer with the correct one above
How many negative solutions are there to the equation below?

How many negative solutions are there to the equation below?
First, subtract 3 from both sides in order to obtain an equation that equals 0:

The left side can be factored. We need factors of  that add up to
that add up to  .
.  and
and  work:
work:

Set both factors equal to 0 and solve:

To solve the left equation, add 1 to both sides. To solve the right equation, subtract 3 from both sides. This yields two solutions:

Only one of these solutions is negative, so the answer is 1.
First, subtract 3 from both sides in order to obtain an equation that equals 0:
The left side can be factored. We need factors of 



Set both factors equal to 0 and solve:
To solve the left equation, add 1 to both sides. To solve the right equation, subtract 3 from both sides. This yields two solutions:
Only one of these solutions is negative, so the answer is 1.
Compare your answer with the correct one above
If the polynomial

is divided by
 ,
,
what is the remainder?
If the polynomial
is divided by

what is the remainder?
By the Remainder Theorem, if a polynomial  is divided by a binomial
is divided by a binomial  , the remainder is
, the remainder is  .
.
Let  . Setting
. Setting  , if
, if  is divided by
is divided by  , the remainder is
, the remainder is  , which can be evaluated by setting
, which can be evaluated by setting  in the definition of
in the definition of  and evaluating:
and evaluating:




By the Remainder Theorem, if a polynomial 


Let 






Compare your answer with the correct one above
If the polynomial

is divided by
 ,
,
what is the remainder?
If the polynomial
is divided by

what is the remainder?
By the Remainder Theorem, if a polynomial  is divided by a binomial
is divided by a binomial  , the remainder is
, the remainder is  .
.
Let  . Setting
. Setting  (since
(since  ), if
), if  is divided by
is divided by  , the remainder is
, the remainder is  , which can be evaluated by setting
, which can be evaluated by setting  in the definition of
in the definition of  and evaluating:
and evaluating:





By the Remainder Theorem, if a polynomial 


Let 







Compare your answer with the correct one above
Which of the following is a factor of the polynomial  ?
?
Which of the following is a factor of the polynomial 
Call 
By the Rational Zeroes Theorem, since  has only integer coefficients, any rational solution of
has only integer coefficients, any rational solution of  must be a factor of 54 divided by a factor of 1 - positive or negative. 54 has as its factors 1, 2, 3, 6, 9, 18, 27 , 54; 1 has only itself as a factor. Therefore, the rational solutions of
must be a factor of 54 divided by a factor of 1 - positive or negative. 54 has as its factors 1, 2, 3, 6, 9, 18, 27 , 54; 1 has only itself as a factor. Therefore, the rational solutions of  must be chosen from this set:
must be chosen from this set:
 .
.
By the Factor Theorem, a polynomial  is divisible by
is divisible by  if and only if
if and only if  - that is, if
- that is, if  is a zero. By the preceding result, we can immediately eliminate
is a zero. By the preceding result, we can immediately eliminate  and
and  as factors, since 12 and 16 have been eliminated as possible zeroes.
as factors, since 12 and 16 have been eliminated as possible zeroes.
Of the three remaining choices, we can demonstrate that  is the factor by evaluating
is the factor by evaluating  :
:





 , so
, so  is a factor.
is a factor.
Of the remaining two choices,  and
and  , both can be proved to not be factors by showing that
, both can be proved to not be factors by showing that  and
and  are both nonzero:
are both nonzero:





 , so
, so  is not a factor.
is not a factor.





 , so
, so  is not a factor.
is not a factor.
Call
By the Rational Zeroes Theorem, since 



By the Factor Theorem, a polynomial 





Of the three remaining choices, we can demonstrate that 



Of the remaining two choices, 







Compare your answer with the correct one above
Solve each problem and decide which is the best of the choices given.
What are the zeros of the following trinomial?

Solve each problem and decide which is the best of the choices given.
What are the zeros of the following trinomial?
First factor out a  . Then the factors of the remaining polynomial,
. Then the factors of the remaining polynomial,
 , are
, are  and
and 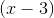 .
.
Set everything equal to zero and you get  ,
,  , and
, and  because you cant forget to set
because you cant forget to set  equal to zero.
equal to zero.
First factor out a 


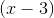
Set everything equal to zero and you get 



Compare your answer with the correct one above
Factor the following variable
(x2 + 18x + 72)
Factor the following variable
(x2 + 18x + 72)
You need to find two numbers that multiply to give 72 and add up to give 18
easiest way: write the multiples of 72:
1, 72
2, 36
3, 24
4, 18
6, 12: these add up to 18
(x + 6)(x + 12)
You need to find two numbers that multiply to give 72 and add up to give 18
easiest way: write the multiples of 72:
1, 72
2, 36
3, 24
4, 18
6, 12: these add up to 18
(x + 6)(x + 12)
Compare your answer with the correct one above
When  is factored, it can be written in the form
is factored, it can be written in the form  , where
, where  ,
,  ,
,  ,
,  ,
,  , and
, and  are all integer constants, and
are all integer constants, and  .
.
What is the value of  ?
?
When 








What is the value of 
Let's try to factor x2 – y2 – z2 + 2yz.
Notice that the last three terms are very close to y2 + z2 – 2yz, which, if we rearranged them, would become y2 – 2yz+ z2. We could factor y2 – 2yz+ z2 as (y – z)2, using the general rule that p2 – 2pq + q2 = (p – q)2 .
So we want to rearrange the last three terms. Let's group them together first.
x2 + (–y2 – z2 + 2yz)
If we were to factor out a –1 from the last three terms, we would have the following:
x2 – (y2 + z2 – 2yz)
Now we can replace y2 + z2 – 2yz with (y – z)2.
x2 – (y – z)2
This expression is actually a differences of squares. In general, we can factor p2 – q2 as (p – q)(p + q). In this case, we can substitute x for p and (y – z) for q.
x2 – (y – z)2 = (x – (y – z))(x + (y – z))
Now, let's distribute the negative one in the trinomial x – (y – z)
(x – (y – z))(x + (y – z))
(x – y + z)(x + y – z)
The problem said that factoring x2 – y2 – z2 + 2yz would result in two polynomials in the form (ax + by + cz)(dx + ey + fz), where a, b, c, d, e, and f were all integers, and a > 0.
(x – y + z)(x + y – z) fits this form. This means that a = 1, b = –1, c = 1, d = 1, e = 1, and f = –1. The sum of all of these is 2.
The answer is 2.
Let's try to factor x2 – y2 – z2 + 2yz.
Notice that the last three terms are very close to y2 + z2 – 2yz, which, if we rearranged them, would become y2 – 2yz+ z2. We could factor y2 – 2yz+ z2 as (y – z)2, using the general rule that p2 – 2pq + q2 = (p – q)2 .
So we want to rearrange the last three terms. Let's group them together first.
x2 + (–y2 – z2 + 2yz)
If we were to factor out a –1 from the last three terms, we would have the following:
x2 – (y2 + z2 – 2yz)
Now we can replace y2 + z2 – 2yz with (y – z)2.
x2 – (y – z)2
This expression is actually a differences of squares. In general, we can factor p2 – q2 as (p – q)(p + q). In this case, we can substitute x for p and (y – z) for q.
x2 – (y – z)2 = (x – (y – z))(x + (y – z))
Now, let's distribute the negative one in the trinomial x – (y – z)
(x – (y – z))(x + (y – z))
(x – y + z)(x + y – z)
The problem said that factoring x2 – y2 – z2 + 2yz would result in two polynomials in the form (ax + by + cz)(dx + ey + fz), where a, b, c, d, e, and f were all integers, and a > 0.
(x – y + z)(x + y – z) fits this form. This means that a = 1, b = –1, c = 1, d = 1, e = 1, and f = –1. The sum of all of these is 2.
The answer is 2.
Compare your answer with the correct one above





