Number Theory - SAT Subject Test in Math II
Card 0 of 20
Define an operation  on the set of real numbers as follows:
on the set of real numbers as follows:
For any two real numbers  ,
,
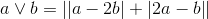 .
.
Evaluate  .
.
Define an operation 
For any two real numbers 
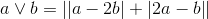
Evaluate 
Substitute  in the expression:
in the expression:



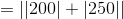



Substitute 
Compare your answer with the correct one above
Which of the following sets is closed under multiplication?
Which of the following sets is closed under multiplication?
A set is closed under multiplication if and only if the product of any two (not necessarily distinct) elements of that set is itself an element of that set.
This can easily be disproved in the case of three of these sets:






But closure can be proved to hold in the case of  . Each number takes the form of
. Each number takes the form of  for some nonnegative integer
for some nonnegative integer  . If we multiply two numbers in this form, we get
. If we multiply two numbers in this form, we get



which is an element of  , being of this form.
, being of this form.
A set is closed under multiplication if and only if the product of any two (not necessarily distinct) elements of that set is itself an element of that set.
This can easily be disproved in the case of three of these sets:
But closure can be proved to hold in the case of 


which is an element of 
Compare your answer with the correct one above

The above represents a Venn diagram. The universal set  is the set of all positive integers.
is the set of all positive integers.
Let  be the set of all multiples of 2; let
be the set of all multiples of 2; let  be the set of all multiples of 3; let
be the set of all multiples of 3; let  be the set of all multiples of 5.
be the set of all multiples of 5.
As you can see, the three sets divide the universal set into eight regions. Suppose each positive integer was placed in the correct region. Which of the following numbers would be in the same region as 873?

The above represents a Venn diagram. The universal set 
Let 


As you can see, the three sets divide the universal set into eight regions. Suppose each positive integer was placed in the correct region. Which of the following numbers would be in the same region as 873?
From the last digit, it can be immediately determined that 873 is not a multple of 2 or 5; since  , 873 is a multiple of 3. Therefore,
, 873 is a multiple of 3. Therefore,

We are looking for an integer that is also in this set - that is, one that is also a multiple of 3 but not 2 or 5. From the last digits, we can immediately eliminate 366 and 368 as multiples of 2 and 365 as a multiple of 5. We test 367 and 369 to see which one is a multiple of 3:


369 is the correct choice.
From the last digit, it can be immediately determined that 873 is not a multple of 2 or 5; since 
We are looking for an integer that is also in this set - that is, one that is also a multiple of 3 but not 2 or 5. From the last digits, we can immediately eliminate 366 and 368 as multiples of 2 and 365 as a multiple of 5. We test 367 and 369 to see which one is a multiple of 3:
369 is the correct choice.
Compare your answer with the correct one above
What is the power set for the data set?

What is the power set for the data set?
The power set is the set of all subsets that can be created from the original set.
For the set  , you can create the subsets:
, you can create the subsets:

This means that the power set is the set of all sets, so the power set is:

The power set is the set of all subsets that can be created from the original set.
For the set 
This means that the power set is the set of all sets, so the power set is:
Compare your answer with the correct one above
Evaluate:

Evaluate:
Use the square of a sum pattern

where  :
:





Use the square of a sum pattern
where 
Compare your answer with the correct one above
Multiply: 
Multiply:
This is the product of a complex number and its complex conjugate. They can be multiplied using the pattern

with 

This is not among the given responses.
This is the product of a complex number and its complex conjugate. They can be multiplied using the pattern
with
This is not among the given responses.
Compare your answer with the correct one above
Multiply:

Multiply:
Compare your answer with the correct one above
Which of the following is equal to  ?
?
Which of the following is equal to 
To raise  to a power, divide the exponent by 4 and note the remainder.
to a power, divide the exponent by 4 and note the remainder.

Raise  to the power of that remainder:
to the power of that remainder:

To raise 
Raise 
Compare your answer with the correct one above
Evaluate:

Evaluate:
Use the square of a sum pattern

where  :
:





Use the square of a sum pattern
where 
Compare your answer with the correct one above
Multiply:

Multiply:
Apply the distributive property:





Apply the distributive property:
Compare your answer with the correct one above
Which of the following is equal to  ?
?
Which of the following is equal to 
By the power of a product property,

By the power of a product property,
Compare your answer with the correct one above
Multiply:

Multiply:
Use the FOIL method:






Use the FOIL method:
Compare your answer with the correct one above
Which of the following is equal to  ?
?
Which of the following is equal to 
To raise  to a power, divide the exponent by 4 and note the remainder.
to a power, divide the exponent by 4 and note the remainder.

Raise  to the power of that remainder:
to the power of that remainder:

To raise 
Raise 
Compare your answer with the correct one above
Multiply:

Multiply:
Apply the distributive property:






Apply the distributive property:
Compare your answer with the correct one above
Multiply:

Multiply:
Compare your answer with the correct one above
 denotes the complex conjugate of
denotes the complex conjugate of  .
.
If  , then evaluate
, then evaluate  .
.


If 

By the difference of squares pattern,

If  , then
, then  .
.
Consequently:






Therefore,

By the difference of squares pattern,
If 

Consequently:
Therefore,
Compare your answer with the correct one above
 is a complex number;
is a complex number;  denotes the complex conjugate of
denotes the complex conjugate of  .
.

Which of the following could be the value of  ?
?



Which of the following could be the value of 
The product of a complex number  and its complex conjugate
and its complex conjugate  is
is

Setting  and
and  accordingly for each of the four choices, we want to find the choice for which
accordingly for each of the four choices, we want to find the choice for which  :
:












For each given value of  ,
,  .
.
The product of a complex number 

Setting 


For each given value of 

Compare your answer with the correct one above
 denotes the complex conjugate of
denotes the complex conjugate of  .
.
If  , then evaluate
, then evaluate  .
.


If 

Applying the Power of a Product Rule:

The complex conjugate of an imaginary number  is
is  ; the product of the two is
; the product of the two is

 , so, setting
, so, setting  in the above pattern:
in the above pattern:

Consequently,

Applying the Power of a Product Rule:
The complex conjugate of an imaginary number 



Consequently,
Compare your answer with the correct one above
Let  and
and  be complex numbers.
be complex numbers.  and
and  denote their complex conjugates.
denote their complex conjugates.


Evaluate  .
.
Let 



Evaluate 
Knowing the actual values of  and
and  is not necessary to solve this problem. The product of the complex conjugates of two numbers is equal to the complex conjugate of the product of the numbers; that is,
is not necessary to solve this problem. The product of the complex conjugates of two numbers is equal to the complex conjugate of the product of the numbers; that is,

We are given that  .
.  is therefore the conjugate of
is therefore the conjugate of  , or
, or  .
.
Knowing the actual values of 

We are given that 



Compare your answer with the correct one above
Let  be a complex number.
be a complex number.  denotes the complex conjugate of
denotes the complex conjugate of  .
.
 and
and  .
.
How many of the following expressions could be equal to  ?
?
(a) 
(b) 
(c) 
(d) 
Let 




How many of the following expressions could be equal to 
(a)
(b)
(c)
(d)
 is a complex number, so
is a complex number, so  for some real
for some real  ; also,
; also,  .
.
Therefore,

Substituting:



Therefore, we can eliminate choices (c) and (d).
Also, the product

Setting  and substituting 10 for
and substituting 10 for  , we get
, we get




Therefore, either  or
or  - making two the correct response.
- making two the correct response.




Therefore,
Substituting:
Therefore, we can eliminate choices (c) and (d).
Also, the product
Setting 

Therefore, either 

Compare your answer with the correct one above






