Graphing Linear Functions - SAT Subject Test in Math II
Card 0 of 1
Question
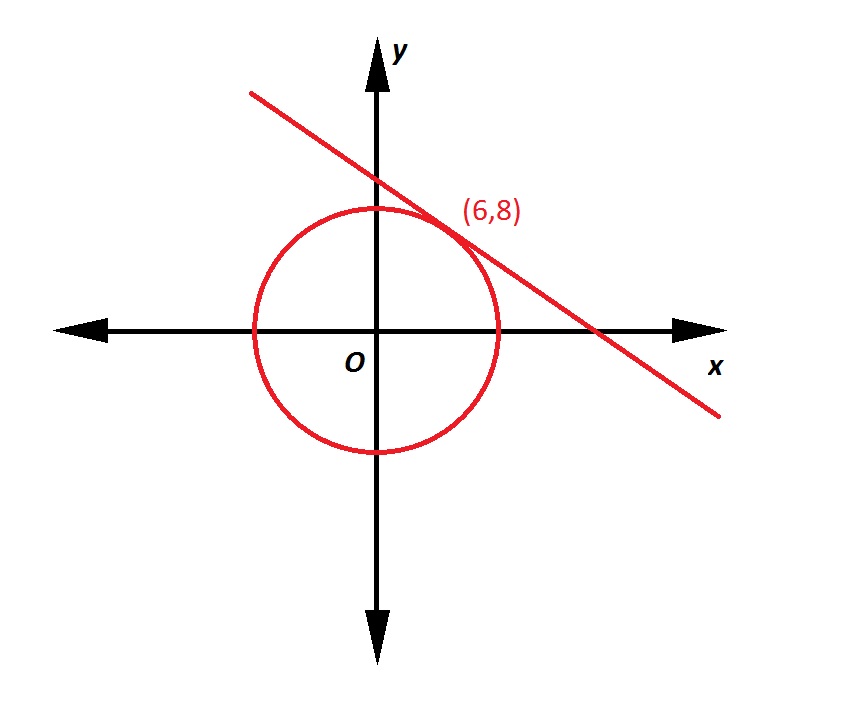
Note: Figure NOT drawn to scale.
Refer to the above figure. The circle has its center at the origin; the line is tangent to the circle at the point indicated. What is the equation of the line in slope-intercept form?
Note: Figure NOT drawn to scale.
Refer to the above figure. The circle has its center at the origin; the line is tangent to the circle at the point indicated. What is the equation of the line in slope-intercept form?
Answer
A line tangent to a circle at a given point is perpendicular to the radius from the center to that point. That radius, which has endpoints 
, has slope
.
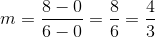The line, being perpendicular to this radius, will have slope equal to the opposite of the reciprocal of that of the radius. This slope will be 
. Since it includes point 
, we can use the point-slope form of the line to find its equation:
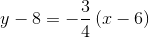
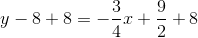
A line tangent to a circle at a given point is perpendicular to the radius from the center to that point. That radius, which has endpoints
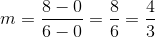
The line, being perpendicular to this radius, will have slope equal to the opposite of the reciprocal of that of the radius. This slope will be
Compare your answer with the correct one above
Tap the card to reveal the answer