Functions and Graphs - SAT Subject Test in Math II
Card 0 of 20
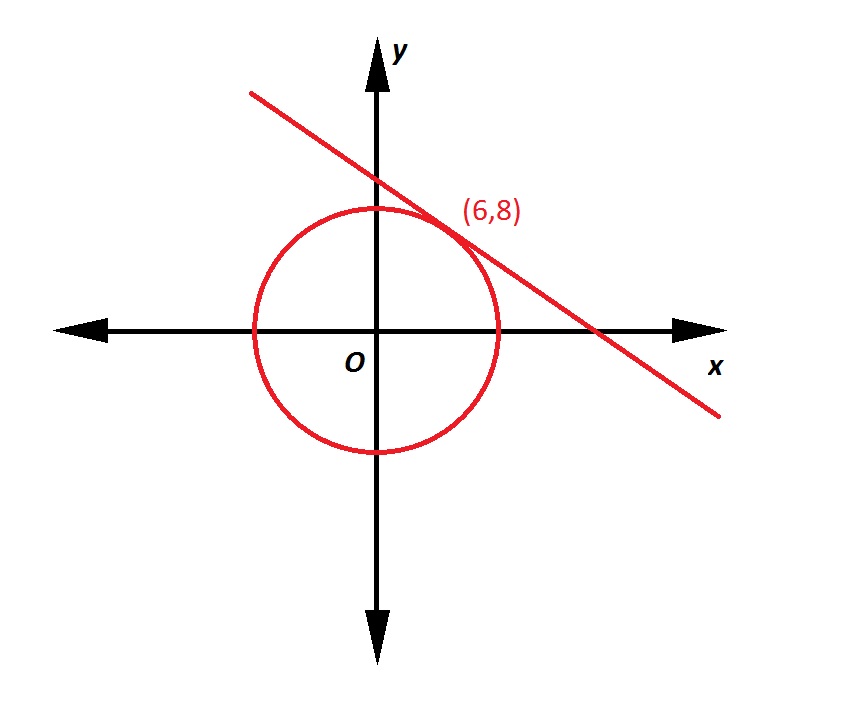
Note: Figure NOT drawn to scale.
Refer to the above figure. The circle has its center at the origin; the line is tangent to the circle at the point indicated. What is the equation of the line in slope-intercept form?

Note: Figure NOT drawn to scale.
Refer to the above figure. The circle has its center at the origin; the line is tangent to the circle at the point indicated. What is the equation of the line in slope-intercept form?
A line tangent to a circle at a given point is perpendicular to the radius from the center to that point. That radius, which has endpoints  , has slope
, has slope
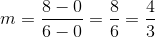 .
.
The line, being perpendicular to this radius, will have slope equal to the opposite of the reciprocal of that of the radius. This slope will be  . Since it includes point
. Since it includes point  , we can use the point-slope form of the line to find its equation:
, we can use the point-slope form of the line to find its equation:

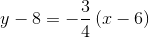

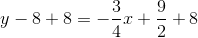

A line tangent to a circle at a given point is perpendicular to the radius from the center to that point. That radius, which has endpoints 
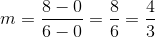
The line, being perpendicular to this radius, will have slope equal to the opposite of the reciprocal of that of the radius. This slope will be 

Compare your answer with the correct one above
Give the period of the graph of the equation

Give the period of the graph of the equation
The period of the graph of a cosine function  is
is 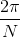 , or
, or 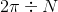
Since  , the period is
, the period is

The period of the graph of a cosine function 
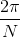
Since 
Compare your answer with the correct one above
Define a function  as follows:
as follows:

At which of the following values of  is
is  discontinuous?
discontinuous?
I) 
II) 
III) 
Define a function 
At which of the following values of 

I)
II)
III)
To determine whether  is continuous at
is continuous at  , we examine the definitions of
, we examine the definitions of  on both sides of
on both sides of  , and evaluate both for
, and evaluate both for  :
:
 evaluated for
evaluated for  :
:

 evaluated for
evaluated for  :
:

Since the values do not coincide,  is discontinuous at
is discontinuous at  .
.
We do the same thing with the other two boundary values 0 and  .
.
 evaluated for
evaluated for  :
:

 evaluated for
evaluated for  :
:

Since the values coincide,  is continuous at
is continuous at  .
.
 turns out to be undefined for
turns out to be undefined for  , (since
, (since  is undefined), so
is undefined), so  is discontinuous at
is discontinuous at  .
.
The correct response is I and III only.
To determine whether 








Since the values do not coincide, 

We do the same thing with the other two boundary values 0 and 




Since the values coincide, 






The correct response is I and III only.
Compare your answer with the correct one above
Define a function  as follows:
as follows:

How many  -intercept(s) does the graph of
-intercept(s) does the graph of  have?
have?
Define a function 
How many 

To find the  -coordinates of possible
-coordinates of possible  -intercepts, set each of the expressions in the definition equal to 0, making sure that the solution is on the interval on which
-intercepts, set each of the expressions in the definition equal to 0, making sure that the solution is on the interval on which  is so defined.
is so defined.
 on the interval
on the interval ![(-\infty, -5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248155/gif.latex)



 or
or 
However, neither value is in the interval ![(-\infty, -5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248161/gif.latex) , so neither is an
, so neither is an  -intercept.
-intercept.
 on the interval
on the interval ![( -5, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248164/gif.latex)



However, this value is not in the interval ![( -5, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248168/gif.latex) , so this is not an
, so this is not an  -intercept.
-intercept.
 on the interval
on the interval ![(0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248171/gif.latex)


However, this value is not in the interval ![(0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248174/gif.latex) , so this is not an
, so this is not an  -intercept.
-intercept.
 on the interval
on the interval 




However, neither value is in the interval  , so neither is an
, so neither is an  -intercept.
-intercept.
The graph of  has no
has no  -intercepts.
-intercepts.
To find the 




However, neither value is in the interval ![(-\infty, -5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248161/gif.latex)


However, this value is not in the interval ![( -5, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248168/gif.latex)


However, this value is not in the interval ![(0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248174/gif.latex)


However, neither value is in the interval 

The graph of 

Compare your answer with the correct one above
Define a function  as follows:
as follows:

How many  -intercept(s) does the graph of
-intercept(s) does the graph of  have?
have?
Define a function 
How many 

To find the  -coordinates of possible
-coordinates of possible  -intercepts, set each of the expressions in the definition equal to 0, making sure that the solution is on the interval on which
-intercepts, set each of the expressions in the definition equal to 0, making sure that the solution is on the interval on which  is so defined.
is so defined.
 on the interval
on the interval ![(-\infty, -5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248099/gif.latex)



However, this value is not in the interval ![( -5, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248103/gif.latex) , so this is not an
, so this is not an  -intercept.
-intercept.
 on the interval
on the interval ![( -5, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248106/gif.latex)



 or
or 
 is on the interval
is on the interval ![( -5, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248113/gif.latex) , so
, so  is an
is an  -intercept.
-intercept.
 on the interval
on the interval ![(0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248117/gif.latex)




 is on the interval
is on the interval ![(0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248123/gif.latex) , so
, so  is an
is an  -intercept.
-intercept.
 on the interval
on the interval 


However, this value is not in the interval  , so this is not an
, so this is not an  -intercept.
-intercept.
The graph has two  -intercepts,
-intercepts,  and
and  .
.
To find the 



However, this value is not in the interval ![( -5, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248103/gif.latex)




![( -5, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248113/gif.latex)




![(0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248123/gif.latex)



However, this value is not in the interval 

The graph has two 


Compare your answer with the correct one above
Define a function  as follows:
as follows:

At which of the following values of  is the graph of
is the graph of  discontinuous?
discontinuous?
I) 
II) 
III) 
Define a function 
At which of the following values of 

I)
II)
III)
To determine whether  is continuous at
is continuous at  , we examine the definitions of
, we examine the definitions of  on both sides of
on both sides of  , and evaluate both for
, and evaluate both for  :
:
 evaluated for
evaluated for  :
:

 evaluated for
evaluated for  :
:

Since the values coincide, the graph of  is continuous at
is continuous at  .
.
We do the same thing with the other two boundary values 0 and 1:
 evaluated for
evaluated for  :
:

 evaluated for
evaluated for  :
:

Since the values do not coincide, the graph of  is discontinuous at
is discontinuous at  .
.
 evaluated for
evaluated for  :
:

 evaluate for
evaluate for  :
:

Since the values do not coincide, the graph of  is discontinuous at
is discontinuous at  .
.
II and III only is the correct response.
To determine whether 








Since the values coincide, the graph of 

We do the same thing with the other two boundary values 0 and 1:




Since the values do not coincide, the graph of 





Since the values do not coincide, the graph of 

II and III only is the correct response.
Compare your answer with the correct one above
Define function  as follows:
as follows:

Give the  -intercept of the graph of the function.
-intercept of the graph of the function.
Define function 
Give the 
To find the  -intercept, evaluate
-intercept, evaluate  using the definition of
using the definition of  on the interval that includes the value 0. Since
on the interval that includes the value 0. Since

on the interval ![(-1, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248051/gif.latex) ,
,
evaluate:

The  -intercept is
-intercept is  .
.
To find the 


on the interval ![(-1, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248051/gif.latex)
evaluate:
The 

Compare your answer with the correct one above
Define a function  as follows:
as follows:

Give the  -intercept of the graph of the function.
-intercept of the graph of the function.
Define a function 
Give the 
To find the  -intercept, evaluate
-intercept, evaluate  using the definition of
using the definition of  on the interval that includes the value 0. Since
on the interval that includes the value 0. Since

on the interval ![(-\pi, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248040/gif.latex) ,
,
evaluate:

The  -intercept is
-intercept is  .
.
To find the 


on the interval ![(-\pi, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/248040/gif.latex)
evaluate:
The 

Compare your answer with the correct one above
What is the center and radius of the circle indicated by the equation?

What is the center and radius of the circle indicated by the equation?
A circle is defined by an equation in the format  .
.
The center is indicated by the point  and the radius
and the radius  .
.
In the equation  , the center is
, the center is  and the radius is
and the radius is  .
.
A circle is defined by an equation in the format 
The center is indicated by the point 

In the equation 


Compare your answer with the correct one above
Give the  -coordinate of the vertex of the parabola of the function
-coordinate of the vertex of the parabola of the function
 .
.
Give the 

The  -coordinate of the vertex of a parabola of the form
-coordinate of the vertex of a parabola of the form

is
 .
.
Set  :
:

The  -coordinate is therefore
-coordinate is therefore  :
:



 , which is the correct choice.
, which is the correct choice.
The 
is

Set 
The 


Compare your answer with the correct one above
Give the axis of symmetry of the parabola of the equation

Give the axis of symmetry of the parabola of the equation
The line of symmetry of the parabola of the equation

is the vertical line

Substitute  :
:
The line of symmetry is

That is, the line of the equation  .
.
The line of symmetry of the parabola of the equation
is the vertical line
Substitute 
The line of symmetry is
That is, the line of the equation 
Compare your answer with the correct one above
Give the  -intercept(s) of the parabola of the equation
-intercept(s) of the parabola of the equation

Give the 
Set  and solve for
and solve for  :
:


The terms have a GCF of 2, so

The trinomial in parentheses can be FOILed out by noting that  and
and  :
:

And you can divide both sides by 3 to get rid of the coefficient:

Set each of the linear binomials to 0 and solve for  :
:

or

The parabola has as its two intercepts the points  and
and  .
.
Set 

The terms have a GCF of 2, so
The trinomial in parentheses can be FOILed out by noting that 

And you can divide both sides by 3 to get rid of the coefficient:
Set each of the linear binomials to 0 and solve for 
or
The parabola has as its two intercepts the points 

Compare your answer with the correct one above
Give the  -coordinate of the vertex of the parabola of the function
-coordinate of the vertex of the parabola of the function

Give the 
The  -coordinate of the vertex of a parabola of the form
-coordinate of the vertex of a parabola of the form

is
 .
.
Substitute  :
:

The  -coordinate is therefore
-coordinate is therefore  :
:





The 
is

Substitute 
The 

Compare your answer with the correct one above
A baseball is thrown straight up with an initial speed of 60 miles per hour by a man standing on the roof of a 100-foot high building. The height of the baseball in feet is modeled by the function

To the nearest foot, how high is the baseball when it reaches the highest point of its path?
A baseball is thrown straight up with an initial speed of 60 miles per hour by a man standing on the roof of a 100-foot high building. The height of the baseball in feet is modeled by the function
To the nearest foot, how high is the baseball when it reaches the highest point of its path?
We are seeking the value of  when the graph of
when the graph of  - a parabola - reaches its vertex.
- a parabola - reaches its vertex.
To find this value, we first find the value of  . For a parabola of the equation
. For a parabola of the equation
 ,
,
the  value of the vertex is
value of the vertex is
 .
.
Substitute  :
:

The height of the baseball after 1.875 seconds will be

 feet.
feet.
We are seeking the value of 

To find this value, we first find the value of 

the 

Substitute 
The height of the baseball after 1.875 seconds will be

Compare your answer with the correct one above
A baseball is thrown upward from the top of a one hundred and fifty-foot-high building. The initial speed of the ball is forty-five miles per hour. The height of the ball after  seconds is modeled by the function
seconds is modeled by the function

How high does the ball get (nearest foot)?
A baseball is thrown upward from the top of a one hundred and fifty-foot-high building. The initial speed of the ball is forty-five miles per hour. The height of the ball after 
How high does the ball get (nearest foot)?
A quadratic function such as  has a parabola as its graph. The high point of the parabola - the vertex - is what we are looking for.
has a parabola as its graph. The high point of the parabola - the vertex - is what we are looking for.
The vertex of a function

has as coordinates
 .
.
The second coordinate is the height and we are looking for this quantity. Since  , setting
, setting  :
:
 seconds for the ball to reach the peak.
seconds for the ball to reach the peak.
The height of the ball at this point is  , which can be evaluated by substitution:
, which can be evaluated by substitution:





Round this to 182 feet.
A quadratic function such as 
The vertex of a function
has as coordinates

The second coordinate is the height and we are looking for this quantity. Since 


The height of the ball at this point is 
Round this to 182 feet.
Compare your answer with the correct one above
Which of the given functions has the greatest amplitude?
Which of the given functions has the greatest amplitude?
The amplitude of a function is the amount by which the graph of the function travels above and below its midline. When graphing a sine function, the value of the amplitude is equivalent to the value of the coefficient of the sine. Similarly, the coefficient associated with the x-value is related to the function's period. The largest coefficient associated with the sine in the provided functions is 2; therefore the correct answer is  .
.
The amplitude is dictated by the coefficient of the trigonometric function. In this case, all of the other functions have a coefficient of one or one-half.
The amplitude of a function is the amount by which the graph of the function travels above and below its midline. When graphing a sine function, the value of the amplitude is equivalent to the value of the coefficient of the sine. Similarly, the coefficient associated with the x-value is related to the function's period. The largest coefficient associated with the sine in the provided functions is 2; therefore the correct answer is 
The amplitude is dictated by the coefficient of the trigonometric function. In this case, all of the other functions have a coefficient of one or one-half.
Compare your answer with the correct one above
Which of these functions has a graph with amplitude 4?
Which of these functions has a graph with amplitude 4?
The functions in each of the choices take the form of a cosine function
 .
.
The graph of a cosine function in this form has amplitude  . Therefore, for this function to have amplitude 4,
. Therefore, for this function to have amplitude 4,  . Of the five choices, only
. Of the five choices, only

matches this description.
The functions in each of the choices take the form of a cosine function

The graph of a cosine function in this form has amplitude 

matches this description.
Compare your answer with the correct one above
Which of the following sine functions has a graph with period of 7?
Which of the following sine functions has a graph with period of 7?
The period of the graph of a sine function  , is
, is  , or
, or  .
.
Therefore, we solve for  :
:



The correct choice is therefore  .
.
The period of the graph of a sine function 


Therefore, we solve for 
The correct choice is therefore 
Compare your answer with the correct one above
Which of these functions has a graph with amplitude  ?
?
Which of these functions has a graph with amplitude 
The functions in each of the choices take the form of a sine function
 .
.
The graph of a sine function in this form has amplitude  . Therefore, for this function to have amplitude 4,
. Therefore, for this function to have amplitude 4,  . Of the five choices, only
. Of the five choices, only

matches this description.
The functions in each of the choices take the form of a sine function

The graph of a sine function in this form has amplitude 

matches this description.
Compare your answer with the correct one above
Give the amplitude of the graph of the function

Give the amplitude of the graph of the function
The amplitude of the graph of a sine function  is
is  . Here,
. Here,  , so this is the amplitude.
, so this is the amplitude.
The amplitude of the graph of a sine function 


Compare your answer with the correct one above

