Properties of Functions and Graphs - SAT Subject Test in Math I
Card 0 of 20
What is the vertex of the following function? Is it a maximum or a minimum?

What is the vertex of the following function? Is it a maximum or a minimum?
The equation of a parabola can be written in vertex form

where 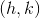 is the vertex and
is the vertex and  determines if it is a minimum or maximum. If
determines if it is a minimum or maximum. If  is positive, then it is a minimum; if
is positive, then it is a minimum; if  is negative, then it is a maximum.
is negative, then it is a maximum.

In this example,  is negative, so the vertex is a maximum.
is negative, so the vertex is a maximum.
 and
and 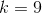

The equation of a parabola can be written in vertex form
where 



In this example, 

Compare your answer with the correct one above
Determine the maximum or minimum of  .
.
Determine the maximum or minimum of 
Rewrite the equation by the order of powers.

This is a parabola in standard form: 
Determine the values of 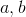 to the vertex formula.
to the vertex formula.

Since the leading coefficient of the parabola is negative, the parabola will curve downward and will have a maximum point.
Therefore there is a maximum at,
 .
.
Rewrite the equation by the order of powers.
This is a parabola in standard form:
Determine the values of 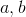
Since the leading coefficient of the parabola is negative, the parabola will curve downward and will have a maximum point.
Therefore there is a maximum at,

Compare your answer with the correct one above
Find the domain:

Find the domain:
To find the domain, find all areas of the number line where the fraction is defined.
 because the denominator of a fraction must be nonzero.
because the denominator of a fraction must be nonzero.
Factor by finding two numbers that sum to -2 and multiply to 1. These numbers are -1 and -1.


To find the domain, find all areas of the number line where the fraction is defined.

Factor by finding two numbers that sum to -2 and multiply to 1. These numbers are -1 and -1.
Compare your answer with the correct one above
The domain includes the values that go into a function (the x-values) and the range are the values that come out (the  or y-values). A sine curve represent a wave the repeats at a regular frequency. Based upon this graph, the maximum
or y-values). A sine curve represent a wave the repeats at a regular frequency. Based upon this graph, the maximum  is equal to 1, while the minimum is equal to –1. The x-values span all real numbers, as there is no limit to the input fo a sine function. The domain of the function is all real numbers and the range is
is equal to 1, while the minimum is equal to –1. The x-values span all real numbers, as there is no limit to the input fo a sine function. The domain of the function is all real numbers and the range is  .
.
The domain includes the values that go into a function (the x-values) and the range are the values that come out (the 


Compare your answer with the correct one above
Give the domain of the function below.

Give the domain of the function below.
The domain is the set of possible value for the  variable. We can find the impossible values of
variable. We can find the impossible values of  by setting the denominator of the fractional function equal to zero, as this would yield an impossible equation.
by setting the denominator of the fractional function equal to zero, as this would yield an impossible equation.

Now we can solve for  .
.


There is no real value of  that will fit this equation; any real value squared will be a positive number.
that will fit this equation; any real value squared will be a positive number.
The radicand is always positive, and  is defined for all real values of
is defined for all real values of  . This makes the domain of
. This makes the domain of  the set of all real numbers.
the set of all real numbers.
The domain is the set of possible value for the 

Now we can solve for 
There is no real value of 
The radicand is always positive, and 


Compare your answer with the correct one above
If  , which of these values of
, which of these values of  is NOT in the domain of this equation?
is NOT in the domain of this equation?

If 

Using  as the input (
as the input ( ) value for this equation generates an output (
) value for this equation generates an output ( ) value that contradicts the stated condition of
) value that contradicts the stated condition of  .
.
Therefore  is not a valid value for
is not a valid value for  and not in the equation's domain:
and not in the equation's domain:

Using 



Therefore 

Compare your answer with the correct one above
Which of the following is NOT a function?
Which of the following is NOT a function?
A function has to pass the vertical line test, which means that a vertical line can only cross the function one time. To put it another way, for any given value of  , there can only be one value of
, there can only be one value of  . For the function
. For the function  , there is one
, there is one  value for two possible
value for two possible  values. For instance, if
values. For instance, if  , then
, then  . But if
. But if  ,
,  as well. This function fails the vertical line test. The other functions listed are a line,
as well. This function fails the vertical line test. The other functions listed are a line, , the top half of a right facing parabola,
, the top half of a right facing parabola,  , a cubic equation,
, a cubic equation,  , and a semicircle,
, and a semicircle,  . These will all pass the vertical line test.
. These will all pass the vertical line test.
A function has to pass the vertical line test, which means that a vertical line can only cross the function one time. To put it another way, for any given value of 












Compare your answer with the correct one above
What is the range of the function?

What is the range of the function?
This function is a parabola that has been shifted up five units. The standard parabola has a range that goes from 0 (inclusive) to positive infinity. If the vertex has been moved up by 5, this means that its minimum has been shifted up by five. The first term is inclusive, which means you need a "\[" for the beginning.
Minimum: 5 inclusive, maximum: infinity
Range: 
This function is a parabola that has been shifted up five units. The standard parabola has a range that goes from 0 (inclusive) to positive infinity. If the vertex has been moved up by 5, this means that its minimum has been shifted up by five. The first term is inclusive, which means you need a "\[" for the beginning.
Minimum: 5 inclusive, maximum: infinity
Range:
Compare your answer with the correct one above
What is the domain of the function?

What is the domain of the function?
The domain represents the acceptable  values for this function. Based on the members of the function, the only limit that you have is the non-allowance of a negative number (because of the square root). The square and the linear terms are fine with any numbers. You cannot have any negative values, otherwise the square root will not be a real number.
values for this function. Based on the members of the function, the only limit that you have is the non-allowance of a negative number (because of the square root). The square and the linear terms are fine with any numbers. You cannot have any negative values, otherwise the square root will not be a real number.
Minimum: 0 inclusive, maximum: infinity
Domain: 
The domain represents the acceptable 
Minimum: 0 inclusive, maximum: infinity
Domain:
Compare your answer with the correct one above
What is the domain of the function?

What is the domain of the function?
There are two limitations in the function: the radical and the denominator term. A radical cannot have a negative term, and a denominator cannot be equal to zero. Based on the first restriction (the radical), our  term must be greater than or equal to zero. Based on the second restriction (the denominator), our
term must be greater than or equal to zero. Based on the second restriction (the denominator), our  term cannot be equal to 4. Our final answer will be the union of these two sets.
term cannot be equal to 4. Our final answer will be the union of these two sets.
Minimum: 0 (inclusive), maximum: infinity
Exclusion: 4
Domain: 
There are two limitations in the function: the radical and the denominator term. A radical cannot have a negative term, and a denominator cannot be equal to zero. Based on the first restriction (the radical), our 

Minimum: 0 (inclusive), maximum: infinity
Exclusion: 4
Domain:
Compare your answer with the correct one above
What is the domain of the function?

What is the domain of the function?
The domain of a function refers to the viable  value inputs. Common domain restrictions involve radicals (which cannot be negative) and fractions (which cannot have a zero denominator).
value inputs. Common domain restrictions involve radicals (which cannot be negative) and fractions (which cannot have a zero denominator).
This function does not have any such restrictions; any value of  will result in a real number. The domain is thus unlimited, ranging from negative infinity to infinity.
will result in a real number. The domain is thus unlimited, ranging from negative infinity to infinity.
Domain: 
The domain of a function refers to the viable 
This function does not have any such restrictions; any value of 
Domain:
Compare your answer with the correct one above
What is the range of the function?

What is the range of the function?
This function represents a parabola that has been shifted 15 units to the left and 2 units up from its standard position.
The vertex of a standard parabola is at (0,0). By shifting the graph as described, the new vertex is at (-15,2). The  value of the vertex represents the minimum of the range; since the parabola opens upward, the maximum will be infinity. Note that the range is inclusive of 2, so you must use a bracket "\[".
value of the vertex represents the minimum of the range; since the parabola opens upward, the maximum will be infinity. Note that the range is inclusive of 2, so you must use a bracket "\[".
Minimum: 2 (inclusive), maximum: infinity
Range: 
This function represents a parabola that has been shifted 15 units to the left and 2 units up from its standard position.
The vertex of a standard parabola is at (0,0). By shifting the graph as described, the new vertex is at (-15,2). The 
Minimum: 2 (inclusive), maximum: infinity
Range:
Compare your answer with the correct one above
What is the domain of the function?

What is the domain of the function?
The domain of a function refers to the viable  value inputs. Common domain restrictions involve radicals (which cannot be negative) and fractions (which cannot have a zero denominator). Both of these restrictions can be found in the given function.
value inputs. Common domain restrictions involve radicals (which cannot be negative) and fractions (which cannot have a zero denominator). Both of these restrictions can be found in the given function.
Let's start with the radical, which must be greater than or equal to zero:


Next, we will look at the fraction denominator, which cannot equal zero:


Our final answer will be the union of the two sets.
Minimum: 2 (inclusive), maximum: infinity
Exclusion: 22
Domain: 
The domain of a function refers to the viable 
Let's start with the radical, which must be greater than or equal to zero:
Next, we will look at the fraction denominator, which cannot equal zero:
Our final answer will be the union of the two sets.
Minimum: 2 (inclusive), maximum: infinity
Exclusion: 22
Domain:
Compare your answer with the correct one above
Find the range of the function  for the domain
for the domain  .
.
Find the range of the function 

The range of a function is the group of corresponding  values for a given domain (
values for a given domain ( values). Plug each
values). Plug each  value into the function to find the range:
value into the function to find the range:




The range is  .
.
The range of a function is the group of corresponding 


The range is 
Compare your answer with the correct one above
Define  .
.
Give the domain of  .
.
Define 
Give the domain of 
The radicand within a square root symbol must be nonnegative, so



This happens if and only if  , so the domain of
, so the domain of  is
is ![[-4,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218946/gif.latex) .
.
The radicand within a square root symbol must be nonnegative, so
This happens if and only if 

![[-4,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218946/gif.latex)
Compare your answer with the correct one above
What is the domain of the following function? Please use interval notation.

What is the domain of the following function? Please use interval notation.
A basic knowledge of absolute value and its functions is valuable for this problem. However, if you do not know what the typical shape of an absoluate value function looks like, one can always plug in  values and plot points.
values and plot points.
Upon doing so, we learn that the  -values (domain) are not restricted on either end of the function, creating a domain of negative infinity to postive infinity.
-values (domain) are not restricted on either end of the function, creating a domain of negative infinity to postive infinity.
If we plug in -100000 for  , we get 100000 for
, we get 100000 for  .
.
If we plug in 100000 for  , we get 100000 for
, we get 100000 for  .
.
Additionally, if we plug in any value for  , we will see that we always get a real, defined value for
, we will see that we always get a real, defined value for  .
.
**Extra Note: Due to the absolute value notation, the negative (-) next to the  is not important, in that it will always be made positive by the absolute value, making this function the same as
is not important, in that it will always be made positive by the absolute value, making this function the same as  . If the negative (-) was outside of the absolute value, this would flip the function, making all corresponding
. If the negative (-) was outside of the absolute value, this would flip the function, making all corresponding  -values negative. However, this knowledge is most important for range, rather than domain.
-values negative. However, this knowledge is most important for range, rather than domain.
A basic knowledge of absolute value and its functions is valuable for this problem. However, if you do not know what the typical shape of an absoluate value function looks like, one can always plug in 
Upon doing so, we learn that the 
If we plug in -100000 for 

If we plug in 100000 for 

Additionally, if we plug in any value for 

**Extra Note: Due to the absolute value notation, the negative (-) next to the 


Compare your answer with the correct one above
What is the range of the following function? Please use interval notation.

What is the range of the following function? Please use interval notation.
A basic knowledge of absolute value and its functions is valuable for this problem. However, if you do not know what the typical shape of an absoluate value function looks like, one can always plug in  values and plot points.
values and plot points.
Upon doing so, we learn that the  -values (range) never surpass
-values (range) never surpass  . This is because of the negative that is placed outside of the absolute value function. Meaning, for every
. This is because of the negative that is placed outside of the absolute value function. Meaning, for every  value we plug in, we will always get a negative value for
value we plug in, we will always get a negative value for  , except when
, except when  .
.
With this knowledge, we can now confidently state the range as ![(-\infty ,0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/244791/gif.latex)
**Extra note: the negative sign outside of the absolute value is simply a transformation of  , reflecting the function about the
, reflecting the function about the  -axis.
-axis.
A basic knowledge of absolute value and its functions is valuable for this problem. However, if you do not know what the typical shape of an absoluate value function looks like, one can always plug in 
Upon doing so, we learn that the 




With this knowledge, we can now confidently state the range as
**Extra note: the negative sign outside of the absolute value is simply a transformation of 

Compare your answer with the correct one above
Define  .
.
Give the range of  .
.
Define 
Give the range of 
The radicand within a square root symbol must be nonnegative, so



This happens if and only if  , so the domain of
, so the domain of  is
is ![[-5,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218954/gif.latex) .
.
 assumes its greatest value when
assumes its greatest value when  , which is the point on
, which is the point on ![[-5,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218957/gif.latex) where
where  is least - this is at
is least - this is at  .
.

Similarly,  assumes its least value when
assumes its least value when  , which is the point on
, which is the point on ![[-5,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218963/gif.latex) where
where  is greatest - this is at
is greatest - this is at  .
.


Therefore, the range of  is
is ![[0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218969/gif.latex) .
.
The radicand within a square root symbol must be nonnegative, so
This happens if and only if 

![[-5,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218954/gif.latex)


![[-5,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218957/gif.latex)


Similarly, 

![[-5,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218963/gif.latex)


Therefore, the range of 
![[0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218969/gif.latex)
Compare your answer with the correct one above
Use the following function and domain to answer this question


Find the range of the function for the given doman. Are  and
and  directly or inversely related?
directly or inversely related?
Use the following function and domain to answer this question
Find the range of the function for the given doman. Are 

To find the range, plug each value of the domain into the equation:





As the x-values increase, the y-values do as well. Therefore there is a  relationship
relationship
To find the range, plug each value of the domain into the equation:
As the x-values increase, the y-values do as well. Therefore there is a 
Compare your answer with the correct one above
A function has the following range:

Which of the following CANNOT be the domain of the function.
A function has the following range:
Which of the following CANNOT be the domain of the function.
Functions cannot have more than one  value for each
value for each  value. This means different numbers in the range cannot be assigned to the same value in the domain. Therefore,
value. This means different numbers in the range cannot be assigned to the same value in the domain. Therefore,  cannot be the domain of the function.
cannot be the domain of the function.
Functions cannot have more than one 


Compare your answer with the correct one above
 is a sine curve. What are the domain and range of this function?
is a sine curve. What are the domain and range of this function?