Polynomials - PSAT Math

Card 0 of 20

Question

Add the polynomials.

$(x^{2}+5x+12) + (3x^{3}+3x+8)$

Answer

We can add together each of the terms of the polynomial which have the same degree for our variable. $(3x^{3}) + (x^{2}) + (5x+3x) + (12+8) = 3x^{3}+x^{2}+8x+20$

Compare your answer with the correct one above

Question

Evaluate the following:

Answer

With this problem, you need to take the trinomials out of parentheses and combine like terms. Since the two trinomials are being added together, you can remove the parentheses without needing to change any signs:

The next step is to combine like terms, based on the variables. You have two terms with , two terms with , and two terms with no variable. Make sure to pay attention to plus and minus signs with each term when combining like terms:

Compare your answer with the correct one above

Question

Evaluate the following:

$\frac{1}{2}(6x^2+2x-3) + \frac{1}{4}(12x^2-24x+6)$

Answer

With this problem, you need to distribute the two fractions across each of the trinomials. To do this, you multiply each term inside the parentheses by the fraction outside of it:

$\frac{1}{2}(6x^2+2x-3) + \frac{1}{4}(12x^2-24x+6)$

$3x^2+x-\frac{3}{2} + 3x^2-6x+\frac{3}{2}$

The next step is to combine like terms, based on the variables. You have two terms with , two terms with , and two terms with no variable. Make sure to pay attention to plus and minus signs with each term when combining like terms. Since you have a positive and negative $\frac{3}{2}$ , those two terms will cancel out:

Compare your answer with the correct one above

Question

Evaluate the following:

$\left(\frac{1}{2}x^2 +2x - 4\right) + \left(\frac{3}{2}x^2 -5x -4\right)$

Answer

To add these two trinomials, you will first begin by combining like terms. You have two terms with , two terms with , and two terms with no variable. For the two fractions with , you can immediately add because they have common denominators:

$(\frac{1}{2}x^2 +2x - 4) + (\frac{3}{2}x^2 -5x -4)$

$\frac{4}{2}x^2 -3x - 8$

Compare your answer with the correct one above

Question

Add:

Answer

To add trinomials, identify and group together the like-terms: . Next, factor out what is common between the like-terms:. Finally, add what is left inside the parentheses to obtain the final answer of .

Compare your answer with the correct one above

Question

Simplify:

Answer

All operations are addition, so we can first remove the parentheses:

Now rearrange the terms so that like terms are next to each other:

Combine like terms:

Compare your answer with the correct one above

Question

Add, expressing the result in simplest form:

$\left ( 4x^{2}+ 9y^{2} \right ) + \left ( 2x^{2}- 4xy + 7y\right )$

Answer

$\left ( 4x^{2}+ 9y^{2} \right ) + \left ( 2x^{2}- 4xy + 7y\right )$

$= 4x^{2}+ 2x^{2} + 9y^{2} - 4xy + 7y$

$= 6x^{2} + 9y^{2} - 4xy + 7y$

Compare your answer with the correct one above

Question

Add, expressing the result in simplest form:

$\left ( 4x^{2}+ 2xy + 7y^{2} \right ) + \left ( 2x^{2}+7y\right )$

Answer

$\left ( 4x^{2}+ 2xy + 7y^{2} \right ) + \left ( 2x^{2}+7y\right )$

$= 4x^{2}+ 2x^{2} + 2xy + 7y^{2} + 7y$

$= 6x^{2} + 2xy + 7y^{2} + 7y$

Compare your answer with the correct one above

Question

Add, expressing the result in simplest form:

$\left ( \frac{1}{2}x^{2} + \frac{2}{3}x - \frac{1}{5}\right ) + \left ( \frac{1}{4}x^{2} - \frac{1}{4}x - \frac{1}{4}\right )$

Answer

$\left ( \frac{1}{2}x^{2} + \frac{2}{3}x - \frac{1}{5}\right ) + \left ( \frac{1}{4}x^{2} - \frac{1}{4}x - \frac{1}{4}\right )$

$= \frac{1}{2}x^{2} + \frac{2}{3}x - \frac{1}{5} + \frac{1}{4}x^{2} - \frac{1}{4}x - \frac{1}{4}$

$= \frac{1}{2}x^{2} + \frac{1}{4}x^{2} + \frac{2}{3}x - \frac{1}{4}x- \frac{1}{5} - \frac{1}{4}$

$=\left ( \frac{1}{2} + \frac{1}{4} \right )x^{2} +\left ( \frac{2}{3} - \frac{1}{4} \right )x- \left (\frac{1}{5}+\frac{1}{4} \right )$

$=\left ( \frac{2}{4} + \frac{1}{4} \right )x^{2} +\left ( \frac{8}{12} - \frac{3}{12} \right )x- \left (\frac{4}{20}+\frac{5}{20} \right )$

$= \frac{3}{4} x^{2} + \frac{5}{12}x - \frac{9}{20}$

Compare your answer with the correct one above

Question

Add, expressing the result in simplest form:

$(0.4x^{2}-0.0006x+ 1)+ (0.03x^{2}+ x - 0.005)$

Answer

$(0.4x^{2}-0.0006x+ 1)+ (0.03x^{2}+ x - 0.005)$

$= 0.4x^{2}+ 0.03x^{2}+ 1x -0.0006x + 1 - 0.005$

$= 0.4 3x^{2} + 0.9994x+ 0.995$

Compare your answer with the correct one above

Question

Find the sum:

Write the answer in standard form.

Answer

Find the sum:

Write the answer in standard form.

Combine like terms:

Write the answer in standard form (terms with the highest degree first):

Compare your answer with the correct one above

Question

If 3 less than 15 is equal to 2x, then 24/x must be greater than

Answer

Set up an equation for the sentence: 15 – 3 = 2x and solve for x. X equals 6. If you plug in 6 for x in the expression 24/x, you get24/6 = 4. 4 is only choice greater than a.

Compare your answer with the correct one above

Question

Given a♦b = (a+b)/(a-b) and b♦a = (b+a)/(b-a), which of the following statement(s) is(are) true:

I. a♦b = -(b♦a)

II. (a♦b)(b♦a) = (a♦b)2

III. a♦b + b♦a = 0

Answer

Notice that - (a-b) = b-a, so statement I & III are true after substituting the expression. Substitute the expression for statement II gives ((a+b)/(a-b))((a+b)/(b-a))=((a+b)(b+a))/((-1)(a-b)(a-b))=-1 〖(a+b)〗2/〖(a-b)〗2 =-((a+b)/(a-b))2 = -(a♦b)2 ≠ (a♦b)2

Compare your answer with the correct one above

Question

If a positive integer a is divided by 7, the remainder is 4. What is the remainder if 3_a_ + 5 is divided by 3?

Answer

The best way to solve this problem is to plug in an appropriate value for a. For example, plug-in 11 for a because 11 divided by 7 will give us a remainder of 4.

Then 3_a + 5_, where a = 11, gives us 38. Then 38 divided by 3 gives a remainder of 2.

The algebra method is as follows:

a divided by 7 gives us some positive integer b, with a remainder of 4.

Thus,

a / 7 = b 4/7

a / 7 = (7_b +_ 4) / 7

a = (7_b_ + 4)

then 3_a + 5 =_ 3 (7_b_ + 4) + 5

(3_a_+5)/3 = \[3(7_b_ + 4) + 5\] / 3

= (7_b_ + 4) + 5/3

The first half of this expression (7_b_ + 4) is a positive integer, but the second half of this expression (5/3) gives us a remainder of 2.

Compare your answer with the correct one above

Question

Answer

Compare your answer with the correct one above

Question

Simplify: $\frac{6x^7y^3z^9}{3x^6y^3z}$

Answer

Cancel by subtracting the exponents of like terms:

$\frac{6x^7y^3z^9}{3x^6y^3z} = 2x^{7-6}y^{3-3}z^{9-1}=2xy^0z^8=2xz^8$

Compare your answer with the correct one above

Question

What is the remainder when the polynomial $x^{4} - 5x^{3} + 3x - 17$ is divided by ?

Answer

By the remainder theorem, if a polynomial is divided by the linear binomial , the remainder is - that is, the polynomial evaluated at . The remainder of dividing $x^{4} - 5x^{3} + 3x - 17$ by is the dividend evaluated at , which is

$x^{4} - 5x^{3} + 3x - 17$

$= 6^{4} - 5 \cdot 6^{3} + 3 \cdot 6 - 17$

$= 1,296 - 5 \cdot 216 + 18 - 17$

Compare your answer with the correct one above

Question

Find the quotient:

$\frac{x^2+6x+9}{x+3}$

Answer

Find the quotient:

$\frac{x^2+6x+9}{x+3}$

Step one: Factor the numerator

$\frac{(x+3)(x+3)}{(x+3)}$

Step two: Simplify

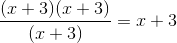
$\frac{(x+3)(x+3)}{(x+3)}= x+3$

Compare your answer with the correct one above

Question

Factor the following expression completely:

Answer

We must begin by factoring out from each term.

Next, we must find two numbers that sum to and multiply to .

Thus, our final answer is:

Compare your answer with the correct one above

Question

Factor the following trinomial:

Answer

To trinomial is in form

In order to factor, find two numbers whose procuct is , in this case , and whose sum is , in this case

Factors of :

Which of these pairs has a sum of ?

and

Therefore the factored form of is:

Compare your answer with the correct one above

Tap the card to reveal the answer