Tetrahedrons - PSAT Math

Card 0 of 6

Question

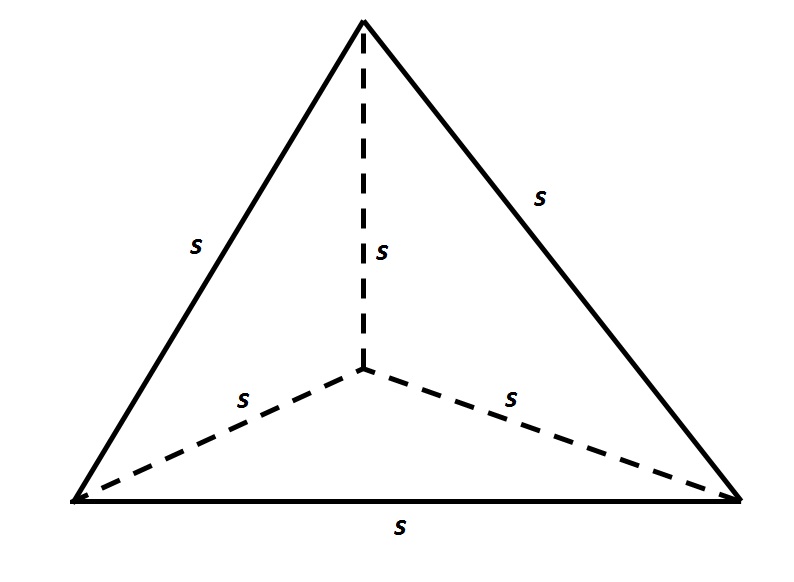
Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate to the nearest tenth.

Answer

The tetrahedron has four faces, each of which is an equilateral triangle with sidelength . Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find , set 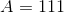in the formula for the area of an equilateral triangle:

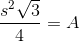
$\frac{s^{2} \sqrt{3} }{4} =A$

$\frac{s^{2} \sqrt{3} }{4} =111$

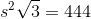
$s^{2} \sqrt{3} =444$

$s^{2}=\frac{444}{ \sqrt{3} } \approx \frac{444}{ 1.732 } \approx 256.34$

$s\approx \sqrt{256.34} \approx 16.0$

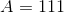
Compare your answer with the correct one above

Question

A regular tetrahedron has four congruent faces, each of which is an equilateral triangle.

A given tetrahedron has edges of length six inches. Give the total surface area of the tetrahedron.

Answer

The area of an equilateral triangle is given by the formula

$A = \frac{s^{2}\sqrt{3}}{4}$

Since there are four equilateral triangles that comprise the surface of the tetrahedron, the total surface area is

$SA = 4 A = 4 \cdot \frac{s^{2}\sqrt{3}}{4} = s^{2}\sqrt{3}$

Substitute :

$SA = s^{2}\sqrt{3} = 6^{2}\sqrt{3} = 36\sqrt{3}$ square inches.

Compare your answer with the correct one above

Question

Give the surface area of the above tetrahedron, or four-faced solid, to the nearest tenth.

Answer

The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 7. Each face has area

$A = \frac{s^{2} \sqrt{3} }{4} = \frac{7^{2} \sqrt{3} }{4} = \frac{49 \sqrt{3} }{4} \approx \frac{49 \cdot 1.7321}{4} \approx 21.22$

The total surface area is four times this, or about $4 \cdot 21.22 = 84.88$ .

Rounded, this is 84.9.

Compare your answer with the correct one above

Question

Note: Figure NOT drawn to scale.

The above triangular pyramid has volume 25. To the nearest tenth, evaluate .

Answer

We are looking for the height of the pyramid.

The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:

$B = \frac{s^{2} \sqrt{3} }{4}$

$B = \frac{4^{2} \sqrt{3} }{4}$

$B = \frac{16 \sqrt{3} }{4}$

$B = 4\sqrt{3}$

The height of a pyramid can be calculated using the fomula

$V = \frac{1}{3}Bh$

We set and $B = 4\sqrt{3}$ and solve for :

$\frac{1}{3} \cdot 4\sqrt{3} \cdot h = 25$

$h = \frac{25 \cdot 3}{4 \sqrt{3}} = \frac{75}{4 \sqrt{3}} \approx \frac{75}{4 \cdot 1.7321} \approx 10.8$

Compare your answer with the correct one above

Question

Note: Figure NOT drawn to scale.

Give the volume (nearest tenth) of the above triangular pyramid.

Answer

The height of the pyramid is . The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:

$B = \frac{s^{2} \sqrt{3} }{4}$

$B = \frac{4^{2} \sqrt{3} }{4}$

$B = \frac{16 \sqrt{3} }{4}$

$B = 4\sqrt{3}$

The volume of a pyramid can be calculated using the fomula

$V = \frac{1}{3}Bh$

$V = \frac{1}{3} \cdot 4\sqrt{3} \cdot 8 = \frac{32\sqrt{3} }{3} \approx \frac{32 \cdot 1.7321}{3} \approx 18.5$

Compare your answer with the correct one above

Question

A regular tetrahedron has an edge length of . What is its volume?

Answer

The volume of a tetrahedron is found with the equation $V=\frac{a^3}{6\sqrt{2}}$ , where represents the length of an edge of the tetrahedron.

Plug in 4 for the edge length and reduce as much as possible to find the answer:

$V=\frac{4^3}{6\sqrt{2}}$

$V=\frac{64}{6\sqrt{2}}$

$V=\frac{32}{3\sqrt{2}}$

The volume of the tetrahedron is $\frac{32}{3\sqrt{2}}$ .

Compare your answer with the correct one above

Tap the card to reveal the answer