How to find the next term in an arithmetic sequence - PSAT Math
Card 0 of 4
A sequence of numbers is as follows:
What is the sum of the first seven numbers in the sequence?
A sequence of numbers is as follows:
What is the sum of the first seven numbers in the sequence?
The pattern of the sequence is (x+1) * 2.
We have the first 5 terms, so we need terms 6 and 7:
(78+1) * 2 = 158
(158+1) * 2 = 318
3 + 8 + 18 +38 + 78 + 158 + 318 = 621
The pattern of the sequence is (x+1) * 2.
We have the first 5 terms, so we need terms 6 and 7:
(78+1) * 2 = 158
(158+1) * 2 = 318
3 + 8 + 18 +38 + 78 + 158 + 318 = 621
Compare your answer with the correct one above
What is the next number in the following series: 0, 3, 8, 15, 24 . . . ?
What is the next number in the following series: 0, 3, 8, 15, 24 . . . ?
The series is defined by n2 – 1 starting at n = 1. The sixth number in the series then equal to 62 – 1 = 35.
The series is defined by n2 – 1 starting at n = 1. The sixth number in the series then equal to 62 – 1 = 35.
Compare your answer with the correct one above
Each term in the sequence is one less than twice the previous term.
So, 
Each term in the sequence is one less than twice the previous term.
So,
Compare your answer with the correct one above
Find the 
term in the sequence
Find the
Notice that in the sequence
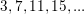
each term increases by 
.
It is always good strategy when attempting to find a pattern in a sequence to examine the difference between each term.
We continue the pattern to find:
The 
term is 
The 
term is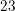 
The 
term is 
It is useful to note that the sequence is defined by,
where n is the number of any one term.
We can solve
to find the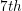 
term.
Notice that in the sequence
each term increases by
It is always good strategy when attempting to find a pattern in a sequence to examine the difference between each term.
We continue the pattern to find:
The
The
The
It is useful to note that the sequence is defined by,
where n is the number of any one term.
We can solve
to find the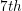
Compare your answer with the correct one above