Solid Geometry - PSAT Math
Card 0 of 20
If a cube is 3” on all sides, what is the length of the diagonal of the cube?
If a cube is 3” on all sides, what is the length of the diagonal of the cube?
General formula for the diagonal of a cube if each side of the cube = s
Use Pythagorean Theorem to get the diagonal across the base:
s2 + s2 = h2
And again use Pythagorean Theorem to get cube’s diagonal, then solve for d:
h2 + s2 = d2
s2 + s2 + s2 = d2
3 * s2 = d2
d = √ (3 * s2) = s √3
So, if s = 3 then the answer is 3√3
General formula for the diagonal of a cube if each side of the cube = s
Use Pythagorean Theorem to get the diagonal across the base:
s2 + s2 = h2
And again use Pythagorean Theorem to get cube’s diagonal, then solve for d:
h2 + s2 = d2
s2 + s2 + s2 = d2
3 * s2 = d2
d = √ (3 * s2) = s √3
So, if s = 3 then the answer is 3√3
Compare your answer with the correct one above
A cube is inscribed in a sphere of radius 1 such that all 8 vertices of the cube are on the surface of the sphere. What is the length of the diagonal of the cube?
A cube is inscribed in a sphere of radius 1 such that all 8 vertices of the cube are on the surface of the sphere. What is the length of the diagonal of the cube?
Since the diagonal of the cube is a line segment that goes through the center of the cube (and also the circumscribed sphere), it is clear that the diagonal of the cube is also the diameter of the sphere. Since the radius = 1, the diameter = 2.
Since the diagonal of the cube is a line segment that goes through the center of the cube (and also the circumscribed sphere), it is clear that the diagonal of the cube is also the diameter of the sphere. Since the radius = 1, the diameter = 2.
Compare your answer with the correct one above
What is the length of the diagonal of a cube with volume of 512 in3?
What is the length of the diagonal of a cube with volume of 512 in3?
The first thing necessary is to determine the dimensions of the cube. This can be done using the volume formula for cubes: V = _s_3, where s is the length of the cube. For our data, this is:
_s_3 = 512, or (taking the cube root of both sides), s = 8.
The distance from corner to corner of the cube will be equal to the distance between (0,0,0) and (8,8,8). The distance formula for three dimensions is very similar to that of 2 dimensions (and hence like the Pythagorean Theorem):
d = √( (_x_1 – _x_2)2 + (_y_1 – _y_2)2 + (_z_1 – _z_2)2)
Or for our simpler case:
d = √( (x)2 + (y)2 + (z)2) = √( (s)2 + (s)2 + (s)2) = √( (8)2 + (8)2 + (8)2) = √( 64 + 64 + 64) = √(64 * 3) = 8√(3)
The first thing necessary is to determine the dimensions of the cube. This can be done using the volume formula for cubes: V = _s_3, where s is the length of the cube. For our data, this is:
_s_3 = 512, or (taking the cube root of both sides), s = 8.
The distance from corner to corner of the cube will be equal to the distance between (0,0,0) and (8,8,8). The distance formula for three dimensions is very similar to that of 2 dimensions (and hence like the Pythagorean Theorem):
d = √( (_x_1 – _x_2)2 + (_y_1 – _y_2)2 + (_z_1 – _z_2)2)
Or for our simpler case:
d = √( (x)2 + (y)2 + (z)2) = √( (s)2 + (s)2 + (s)2) = √( (8)2 + (8)2 + (8)2) = √( 64 + 64 + 64) = √(64 * 3) = 8√(3)
Compare your answer with the correct one above
What is the length of the diagonal of a cube with volume of 1728 in3?
What is the length of the diagonal of a cube with volume of 1728 in3?
The first thing necessary is to determine the dimensions of the cube. This can be done using the volume formula for cubes: V = _s_3, where s is the length of the cube. For our data, this is:
_s_3 = 1728, or (taking the cube root of both sides), s = 12.
The distance from corner to corner of the cube will be equal to the distance between (0,0,0) and (12,12,12). The distance formula for three dimensions is very similar to that of 2 dimensions (and hence like the Pythagorean theorem):
d = √( (_x_1 – _x_2)2 + (_y_1 – _y_2)2 + (_z_1 – _z_2)2)
Or, for our simpler case:
d = √( (x)2 + (y)2 + (z)2) = √( (s)2 + (s)2 + (s)2) = √( (12)2 + (12)2 + (12)2) = √( 144 + 144 + 144) = √(3 * 144) = 12√(3) = 12√(3)
The first thing necessary is to determine the dimensions of the cube. This can be done using the volume formula for cubes: V = _s_3, where s is the length of the cube. For our data, this is:
_s_3 = 1728, or (taking the cube root of both sides), s = 12.
The distance from corner to corner of the cube will be equal to the distance between (0,0,0) and (12,12,12). The distance formula for three dimensions is very similar to that of 2 dimensions (and hence like the Pythagorean theorem):
d = √( (_x_1 – _x_2)2 + (_y_1 – _y_2)2 + (_z_1 – _z_2)2)
Or, for our simpler case:
d = √( (x)2 + (y)2 + (z)2) = √( (s)2 + (s)2 + (s)2) = √( (12)2 + (12)2 + (12)2) = √( 144 + 144 + 144) = √(3 * 144) = 12√(3) = 12√(3)
Compare your answer with the correct one above
What is the length of the diagonal of a cube with surface area of 294 in2?
What is the length of the diagonal of a cube with surface area of 294 in2?
The first thing necessary is to determine the dimensions of the cube. This can be done using the surface area formula for cubes: A = 6_s_2, where s is the length of the cube. For our data, this is:
6_s_2 = 294
_s_2 = 49
(taking the square root of both sides) s = 7
The distance from corner to corner of the cube will be equal to the distance between (0,0,0) and (7,7,7). The distance formula for three dimensions is very similar to that of 2 dimensions (and hence like the Pythagorean Theorem):
d = √((_x_1 – _x_2)2 + (_y_1 – _y_2)2 + (_z_1 – _z_2)2)
Or for our simpler case:
d = √((x)2 + (y)2 + (z)2) = √( (s)2 + (s)2 + (s)2) = √( (7)2 + (7)2 + (7)2) = √( 49 + 49 + 49) = √(49 * 3) = 7√(3)
The first thing necessary is to determine the dimensions of the cube. This can be done using the surface area formula for cubes: A = 6_s_2, where s is the length of the cube. For our data, this is:
6_s_2 = 294
_s_2 = 49
(taking the square root of both sides) s = 7
The distance from corner to corner of the cube will be equal to the distance between (0,0,0) and (7,7,7). The distance formula for three dimensions is very similar to that of 2 dimensions (and hence like the Pythagorean Theorem):
d = √((_x_1 – _x_2)2 + (_y_1 – _y_2)2 + (_z_1 – _z_2)2)
Or for our simpler case:
d = √((x)2 + (y)2 + (z)2) = √( (s)2 + (s)2 + (s)2) = √( (7)2 + (7)2 + (7)2) = √( 49 + 49 + 49) = √(49 * 3) = 7√(3)
Compare your answer with the correct one above
A rectangular prism has a volume of 144 and a surface area of 192. If the shortest edge is 3, what is the length of the longest diagonal through the prism?
A rectangular prism has a volume of 144 and a surface area of 192. If the shortest edge is 3, what is the length of the longest diagonal through the prism?
The volume of a rectangular prism is 
.
We are told that the shortest edge is 3. Let us call this the height.
We now have 
, or 
.
Now we replace variables by known values:
Now we have:
We have thus determined that the other two edges of the rectangular prism will be 4 and 12. We now need to find the longest diagonal. This is equal to:
If you do not remember how to find this directly, you can also do it in steps. You first find the diagonal across one of the sides (in the plane), by using the Pythagorean Theorem. For example, we choose the side with edges 3 and 4. This diagonal will be:
We then use a plane with one side given by the diagonal we just found (length 5) and the other given by the distance of the 3rd edge (length 12).
This diagonal is then 
.
The volume of a rectangular prism is
We are told that the shortest edge is 3. Let us call this the height.
We now have
Now we replace variables by known values:
Now we have:
We have thus determined that the other two edges of the rectangular prism will be 4 and 12. We now need to find the longest diagonal. This is equal to:
If you do not remember how to find this directly, you can also do it in steps. You first find the diagonal across one of the sides (in the plane), by using the Pythagorean Theorem. For example, we choose the side with edges 3 and 4. This diagonal will be:
We then use a plane with one side given by the diagonal we just found (length 5) and the other given by the distance of the 3rd edge (length 12).
This diagonal is then
Compare your answer with the correct one above
A rectangular prism has length 7, width 4, and height 4. What is the distance from the top back left corner to the bottom front right corner?
A rectangular prism has length 7, width 4, and height 4. What is the distance from the top back left corner to the bottom front right corner?
The diagonal from the top back left corner to the bottom front right corner will be the hypotenuse of a right triangle. The sides of the triangle will be the height of the box and the diagonal through the middle of one of the rectangular faces. We will be able to solve for the length using the Pythagorean Theorem.
To calculate the length of the hypotenuse, we first must find the length of the rectangular diagonal using the sides of the rectangle. This diagonal will be the hypotenuse of a right triangle with sides 7 and 4. Solve for the diagonal length using the Pythagorean Theorem.
Now we can return to our first triangle. We are given the height, 4, and now have the length of the rectangular diagonal. Use these values to solve for the length of the diagonal that connects the top back left corner and the bottom front right corner.
The diagonal from the top back left corner to the bottom front right corner will be the hypotenuse of a right triangle. The sides of the triangle will be the height of the box and the diagonal through the middle of one of the rectangular faces. We will be able to solve for the length using the Pythagorean Theorem.
To calculate the length of the hypotenuse, we first must find the length of the rectangular diagonal using the sides of the rectangle. This diagonal will be the hypotenuse of a right triangle with sides 7 and 4. Solve for the diagonal length using the Pythagorean Theorem.
Now we can return to our first triangle. We are given the height, 4, and now have the length of the rectangular diagonal. Use these values to solve for the length of the diagonal that connects the top back left corner and the bottom front right corner.
Compare your answer with the correct one above
The dimensions of a right, rectangular prism are 4 in x 12 in x 2 ft. What is the diagonal distance of the prism?
The dimensions of a right, rectangular prism are 4 in x 12 in x 2 ft. What is the diagonal distance of the prism?
The problem is simple, but be careful. The units are not equal. First convert the last dimension into inches. There are 12 inches per foot. Therefore, the prism's dimensions really are: 4 in x 12 in x 24 in.
From this point, things are relatively easy. The distance from corner to corner in a three-dimensional prism like this can be found by using a variation on the Pythagorean Theorem that merely adds one dimension. That is, _d_2 = _x_2 + _y_2 + _z_2, or d = √(_x_2 + _y_2 + _z_2)
For our data, this would be:
d = √(42 + 122 + 242) = √(16 + 144 + 576) = √(736) = √(2 * 2 * 2 * 2 * 2 * 23) = 4√(46)
The problem is simple, but be careful. The units are not equal. First convert the last dimension into inches. There are 12 inches per foot. Therefore, the prism's dimensions really are: 4 in x 12 in x 24 in.
From this point, things are relatively easy. The distance from corner to corner in a three-dimensional prism like this can be found by using a variation on the Pythagorean Theorem that merely adds one dimension. That is, _d_2 = _x_2 + _y_2 + _z_2, or d = √(_x_2 + _y_2 + _z_2)
For our data, this would be:
d = √(42 + 122 + 242) = √(16 + 144 + 576) = √(736) = √(2 * 2 * 2 * 2 * 2 * 23) = 4√(46)
Compare your answer with the correct one above
The base of a right, rectangular prism is a square. Its height is three times that of one of the sides of the base. If its overall volume is 375 in3, what is the diagonal distance of the prism?
The base of a right, rectangular prism is a square. Its height is three times that of one of the sides of the base. If its overall volume is 375 in3, what is the diagonal distance of the prism?
First, let's represent our dimensions. We know the bottom could be represented as being x by x. The height is said to be three times one of these dimensions, so let's call it 3_x_. Based on this, we know the dimensions of the prism are x, x, and 3_x_. Now, the volume of a right rectangular prism is found by multiplying together its three dimensions. Therefore, if we know the overall volume is 375 in3, we can say:
375 = x * x * 3_x_ or 375 = 3_x_3
Simplifying, we first divide by 3: 125 = _x_3. Taking the cube root of both sides, we find that x = 5.
Now, be careful. The dimensions are not 5, 5, 5. They are (recall) x, x, and 3_x_. If x = 5, this means the dimensions are 5, 5, and 15.
At this point, things are beginning to progress to the end of the problem. The distance from corner to corner in a three-dimensional prism like this can be found by using a variation on the Pythagorean Theorem that merely adds one dimension. That is, _d_2 = _x_2 + _y_2 + _z_2, or d = √(_x_2 + _y_2 + _z_2)
For our data, this would be: d = √(52 + 52 + 152) = √(25 + 25 + 225) = √(275) = √(5 * 5 * 11) = 5√(11) in
First, let's represent our dimensions. We know the bottom could be represented as being x by x. The height is said to be three times one of these dimensions, so let's call it 3_x_. Based on this, we know the dimensions of the prism are x, x, and 3_x_. Now, the volume of a right rectangular prism is found by multiplying together its three dimensions. Therefore, if we know the overall volume is 375 in3, we can say:
375 = x * x * 3_x_ or 375 = 3_x_3
Simplifying, we first divide by 3: 125 = _x_3. Taking the cube root of both sides, we find that x = 5.
Now, be careful. The dimensions are not 5, 5, 5. They are (recall) x, x, and 3_x_. If x = 5, this means the dimensions are 5, 5, and 15.
At this point, things are beginning to progress to the end of the problem. The distance from corner to corner in a three-dimensional prism like this can be found by using a variation on the Pythagorean Theorem that merely adds one dimension. That is, _d_2 = _x_2 + _y_2 + _z_2, or d = √(_x_2 + _y_2 + _z_2)
For our data, this would be: d = √(52 + 52 + 152) = √(25 + 25 + 225) = √(275) = √(5 * 5 * 11) = 5√(11) in
Compare your answer with the correct one above
The base of a right, rectangular prism has one side that is three times the length of the other. Its height is twice the length of the longer side of the base. If its overall volume is 13,122 in3, what is the diagonal distance of the prism?
The base of a right, rectangular prism has one side that is three times the length of the other. Its height is twice the length of the longer side of the base. If its overall volume is 13,122 in3, what is the diagonal distance of the prism?
First, let's represent our dimensions. We know the bottom could be represented as being x by 3_x_. The height is said to be twice the longer dimension, so let's call it 2 * 3_x_, or 6_x_. Based on this, we know the dimensions of the prism are x, 2_x_, and 6_x_. Now, the volume of a right rectangular prism is found by multiplying together its three dimensions. Therefore, if we know the overall volume is 13,122 in3, we can say:
13,122 = x * 3_x_ * 6_x_ or 13,122 = 18_x_3
Simplifying, we first divide by 18: 729 = _x_3. Taking the cube root of both sides, we find that x = 9.
Now, be careful. The dimensions are not 9, 9, and 9. They are (recall) x, 3_x_, and 6_x_. If x = 9, this means the dimensions are 9, 27, and 54.
At this point, things are beginning to progress to the end of the problem. The distance from corner to corner in a three-dimensional prism like this can be found by using a variation on the Pythagorean Theorem that merely adds one dimension. That is, _d_2 = _x_2 + _y_2 + _z_2, or d = √(_x_2 + _y_2 + _z_2)
For our data, this would be: d = √(92 + 272 + 542) = √(81 + 729 + 2916) = √(3726) = √(2 * 3 * 3 * 3 * 3 * 23) = 9√(46) in.
First, let's represent our dimensions. We know the bottom could be represented as being x by 3_x_. The height is said to be twice the longer dimension, so let's call it 2 * 3_x_, or 6_x_. Based on this, we know the dimensions of the prism are x, 2_x_, and 6_x_. Now, the volume of a right rectangular prism is found by multiplying together its three dimensions. Therefore, if we know the overall volume is 13,122 in3, we can say:
13,122 = x * 3_x_ * 6_x_ or 13,122 = 18_x_3
Simplifying, we first divide by 18: 729 = _x_3. Taking the cube root of both sides, we find that x = 9.
Now, be careful. The dimensions are not 9, 9, and 9. They are (recall) x, 3_x_, and 6_x_. If x = 9, this means the dimensions are 9, 27, and 54.
At this point, things are beginning to progress to the end of the problem. The distance from corner to corner in a three-dimensional prism like this can be found by using a variation on the Pythagorean Theorem that merely adds one dimension. That is, _d_2 = _x_2 + _y_2 + _z_2, or d = √(_x_2 + _y_2 + _z_2)
For our data, this would be: d = √(92 + 272 + 542) = √(81 + 729 + 2916) = √(3726) = √(2 * 3 * 3 * 3 * 3 * 23) = 9√(46) in.
Compare your answer with the correct one above
In the rectangular prism above, the length of 
, 
, and 
. What is the length of 
?
In the rectangular prism above, the length of
The equation for the diagonal of a rectangular prism is
Diagonal=
When you plug in the values for the length, width, and height, you get
Diagonal=
Diagonal=
Diagonal=
Diagonal=
The equation for the diagonal of a rectangular prism is
Diagonal=
When you plug in the values for the length, width, and height, you get
Diagonal=
Diagonal=
Diagonal=
Diagonal=
Compare your answer with the correct one above
If a sphere has an approximate volume of 
, then what is the approximate diameter of this sphere?
If a sphere has an approximate volume of
The formula for the volume of a sphere is
Therefore,
Dividing both sides by 
, leaves us with 
. Taking the cube root, we find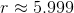 
, meaning our diameter 
.
The formula for the volume of a sphere is
Therefore,
Dividing both sides by
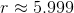
Compare your answer with the correct one above
The number of square units in the surface area of a cube is twice as large as the number of cubic units in its volume. What is the cube's volume, in cubic units?
The number of square units in the surface area of a cube is twice as large as the number of cubic units in its volume. What is the cube's volume, in cubic units?
The number of square units in the surface area of a cube is given by the formula 6s2, where s is the length of the side of the cube in units. Moreover, the number of cubic units in a cube's volume is equal to s3.
Since the number of square units in the surface area is twice as large as the cubic units of the volume, we can write the following equation to solve for s:
6s2 = 2s3
Subtract 6s2 from both sides.
2s3 – 6s2 = 0
Factor out 2s2 from both terms.
2s2(s – 3) = 0
We must set each factor equal to zero.
2s2 = 0, only if s = 0; however, no cube has a side length of zero, so s can't be zero.
Set the other factor, s – 3, equal to zero.
s – 3 = 0
Add three to both sides.
s = 3
This means that the side length of the cube is 3 units. The volume, which we previously stated was equal to s3, must then be 33, or 27 cubic units.
The answer is 27.
The number of square units in the surface area of a cube is given by the formula 6s2, where s is the length of the side of the cube in units. Moreover, the number of cubic units in a cube's volume is equal to s3.
Since the number of square units in the surface area is twice as large as the cubic units of the volume, we can write the following equation to solve for s:
6s2 = 2s3
Subtract 6s2 from both sides.
2s3 – 6s2 = 0
Factor out 2s2 from both terms.
2s2(s – 3) = 0
We must set each factor equal to zero.
2s2 = 0, only if s = 0; however, no cube has a side length of zero, so s can't be zero.
Set the other factor, s – 3, equal to zero.
s – 3 = 0
Add three to both sides.
s = 3
This means that the side length of the cube is 3 units. The volume, which we previously stated was equal to s3, must then be 33, or 27 cubic units.
The answer is 27.
Compare your answer with the correct one above
What is the surface area of a cube whose volume is 512 cubic feet?
What is the surface area of a cube whose volume is 512 cubic feet?
In order to find the surface area of a cube, we need to solve for the length of each side, 
.
Recall the formula for volume: 
Plug in what we know and solve for 
:
Now plug this value into the surface area formula:
In order to find the surface area of a cube, we need to solve for the length of each side,
Recall the formula for volume:
Plug in what we know and solve for
Now plug this value into the surface area formula:
Compare your answer with the correct one above
If the volume of a cube is 64 cubic inches, then it has an edge length of _______.
If the volume of a cube is 64 cubic inches, then it has an edge length of _______.
Compare your answer with the correct one above
If the volume of a cube is 512 units, what is the length of one edge of the cube?
If the volume of a cube is 512 units, what is the length of one edge of the cube?
The volume of a cube is length x width x height. Since it's a cube, though, the length, width, and height are all equal, and equivalent to the length of one edge of the cube. Therefore, to find the lenght of an edge of the cube, just find the cube root of the volume. In this case, the cube root of 512 is equal to 8.
The volume of a cube is length x width x height. Since it's a cube, though, the length, width, and height are all equal, and equivalent to the length of one edge of the cube. Therefore, to find the lenght of an edge of the cube, just find the cube root of the volume. In this case, the cube root of 512 is equal to 8.
Compare your answer with the correct one above
Find the length of an edge of a cube that has a volume of 
.
Find the length of an edge of a cube that has a volume of
All the edges of a cube have the same length, and the volume of a cube is the length of an edge taken to the third power.
So if we take the edge of the cube to be of length x, then:
So the length of the edge of a cube with a volume of 125 is 5.
All the edges of a cube have the same length, and the volume of a cube is the length of an edge taken to the third power.
So if we take the edge of the cube to be of length x, then:
So the length of the edge of a cube with a volume of 125 is 5.
Compare your answer with the correct one above
A certain shipping company has cubic boxes. One of these boxes has a volume of 
. How long are each of the sides of the box in feet?
A certain shipping company has cubic boxes. One of these boxes has a volume of
The formula for the volume of a cube is
where 
is the length of a side.
Here, the volume is 729. To find the side length, take the cube root of both sides:
The cube root of 729 is 9, so the length of each side of the cube is 9 feet.
The formula for the volume of a cube is
where
Here, the volume is 729. To find the side length, take the cube root of both sides:
The cube root of 729 is 9, so the length of each side of the cube is 9 feet.
Compare your answer with the correct one above
If a cube has a volume of 
cubic inches, approximately how long, in feet, is one edge of the cube?
If a cube has a volume of
The formula for the volume of a cube is 
where s is any edge.
This means one edge of the cube is 
. We then divide 8.5 by 12 to convert to feet.
feet.
The formula for the volume of a cube is
This means one edge of the cube is
Compare your answer with the correct one above
For a box to fit inside the cupboard, the sum of the height and the perimeter of the box must, at most, be 360 cm. If Jenn has a box that has a height of 40 cm and a length of 23 cm, what is the greatest possible width of the box?
For a box to fit inside the cupboard, the sum of the height and the perimeter of the box must, at most, be 360 cm. If Jenn has a box that has a height of 40 cm and a length of 23 cm, what is the greatest possible width of the box?
First we write out the equation we are given. H + (2_L_ +2_W_) = 360. H = 40 and L = 23
40 + (2(23) + 2_W_) = 360
40 + (46 + 2_W_) = 360
46 + 2_W_ = 320
2_W_ = 274
W = 137
First we write out the equation we are given. H + (2_L_ +2_W_) = 360. H = 40 and L = 23
40 + (2(23) + 2_W_) = 360
40 + (46 + 2_W_) = 360
46 + 2_W_ = 320
2_W_ = 274
W = 137
Compare your answer with the correct one above