Complex Numbers - PSAT Math

Card 0 of 20

Question

Simplify by rationalizing the denominator:

$\frac{20 + 6i}{8i}$

Answer

Multiply both numerator and denominator by :

$\frac{20 + 6i}{8i}$

$=\frac{\left (20 + 6i \right ) \cdot i}{8i \cdot i}$

$=\frac{ 20i + 6i^{2} }{8i ^{2}}$

$=\frac{ 20i + 6(-1) }{8 (-1)}$

$=\frac{ 20i -6 }{-8}$

$=\frac{ -6+ 20i }{-8}$

$=\frac{ -6 }{-8} + \frac{ 20i }{-8}$

$=\frac{ 3 }{4} - \frac{ 5}{2}i$

Compare your answer with the correct one above

Question

Divide:

$-100 \div 5i$

Answer

Rewrite in fraction form, and multiply both numerator and denominator by :

$-100 \div 5i$

$= \frac{-100}{5i}$

$= \frac{-100 \cdot i }{5i \cdot i }$

$= \frac{-100 i }{5i ^{2}}$

$= \frac{-100 i }{5 (-1)}$

$= \frac{-100 i }{-5}$

$= \frac{-100 }{-5}\cdot i$

Compare your answer with the correct one above

Question

Simplify by rationalizing the denominator:

$\frac{ 25- 12i}{ - 10i}$

Answer

Multiply both numerator and denominator by :

$\frac{ 25- 12i}{ - 10i}$

$=\frac{\left ( 25- 12i \right )\cdot i}{ - 10i \cdot i }$

$=\frac{ 25i- 12i ^{2} }{ - 10i ^{2} }$

$=\frac{ 25i- 12 (-1)}{ - 10 (-1) }$

$=\frac{ 25i+ 12}{ 10}$

$=\frac{12+ 25i }{ 10}$

$=\frac{12 }{ 10} + \frac{ 25i }{ 10}$

$=\frac{6}{ 5} + \frac{ 5 }{ 2}i$

Compare your answer with the correct one above

Question

Simplify by rationalizing the denominator:

$\frac{ 21i}{3+ i\sqrt{5}}$

Answer

Multiply the numerator and the denominator by the complex conjugate of the denominator, which is $3- i\sqrt{5}$ :

$\frac{ 21i}{3+ i\sqrt{5}}$

$= \frac{ 21i\left (3- i\sqrt{5} \right )}{\left (3+ i\sqrt{5} \right )\left (3- i\sqrt{5} \right )}$

$= \frac{21i \cdot 3- 21i \cdot i\sqrt{5} }{ 3^{2}+ \left ( \sqrt{5} \right )^{2}}$

$= \frac{ 63i - 21i^{2} \sqrt{5}}{ 9+5}$

$= \frac{ 63i - 21 (-1)\sqrt{5}}{ 14}$

$= \frac{ 21 \sqrt{5}+ 63i }{ 14}$

$= \frac{ 21 \sqrt{5} }{ 14}+ \frac{63 i}{ 14}$

$= \frac{ 3\sqrt{5} }{ 2} + \frac{ 9 }{ 2} i$

Compare your answer with the correct one above

Question

Simplify by rationalizing the denominator:

$\frac{2+3i}{4+ 3i}$

Answer

Multiply the numerator and the denominator by the complex conjugate of the denominator, which is :

$\frac{2+3i}{4+ 3i}$

$=\frac{\left (2+3i \right )\left (4-3i \right )}{\left (4+ 3i \right )\left (4-3i \right )}$

$=\frac{2 \cdot 4 - 2 \cdot 3i +3i \cdot 4 - 3i \cdot 3i }{4^{2}+3^{2}}$

$=\frac{8 - 6i +12i - 9 i ^{2}}{16+ 9}$

$=\frac{8 - 6i +12i - 9(-1)}{25}$

$=\frac{8 - 6i +12i +9}{25}$

$=\frac{17 + 6i }{25}$

$=\frac{17 }{25} + \frac{ 6 }{25} i$

Compare your answer with the correct one above

Question

Simplify by rationalizing the denominator:

$\frac{15i}{4- 3i}$

Answer

Multiply the numerator and the denominator by the complex conjugate of the denominator, which is :

$\frac{15i}{4- 3i}$

$= \frac{15i\left (4+ 3i \right )}{\left (4- 3i \right )\left (4+ 3i \right )}$

$= \frac{15i\cdot 4+ 15i\cdot 3i }{4^{2}+3^{2}}$

$= \frac{60 i + 45i^{2} }{16+9}$

$= \frac{60 i + 45 (-1)}{25}$

$= \frac{-45 + 60 i}{25}$

$= \frac{-45 }{25} + \frac{ 60 i}{25}$

$= - \frac{9}{5} + \frac{ 12}{5}i$

Compare your answer with the correct one above

Question

Define an operation $\ast$ as follows:

For all complex numbers ,

$a \ast b = \frac{ab}{i}$ .

Evaluate $(3+ 4i) \ast (4-3i)$ .

Answer

$a \ast b = \frac{ab}{i}$

$(3+ 4i) \ast (4-3i)= \frac{(3+ 4i) (4-3i)}{i}$

$= \frac{ 3 \cdot 4 - 3 \cdot 3i + 4i \cdot 4 -4i \cdot 3i}{i}$

$= \frac{ 12 - 9i + 16i -12i ^{2}}{i}$

$= \frac{ 12 - 9i + 16i -12 (-1)}{i}$

$= \frac{ 12 - 9i + 16i +12}{i}$

$= \frac{ 24+7i }{i}$

$= \frac{ \left (24+7i \right ) (-i)}{i (-i)}$

$= \frac{ -24i-7i ^{2} }{ -i^{2}}$

$= \frac{ -24i-7(-1) }{ -(-1)}}$

$= \frac{ -24i+7 }{ 1}$

Compare your answer with the correct one above

Question

Define an operation $\ast$ as follows:

For all complex numbers ,

$a \ast b = \frac{ai}{b}$ .

Evaluate $(2+ i) \ast (2-i)$ .

Answer

$a \ast b = \frac{ai}{b}$

$(2+ i) \ast (2-i)= \frac{(2+ i)i}{2-i}$

$= \frac{2i+ i^{2}}{2-i}$

$= \frac{2i+ (-1)}{2-i}$

$= \frac{-1+2i }{2-i}$

Multiply the numerator and the denominator by the complex conjugate of the denominator, which is . The above becomes:

$\frac{\left (-1+2i \right )\left (2+i \right )}{\left (2-i \right )\left (2+i \right )}$

$= \frac{-1\cdot 2 + (-1)\cdot i + 2i \cdot 2 + 2i \cdot i }{2^{2}+1^{2}}$

$= \frac{-2 +\left (-i \right )+ 4i + 2i^{2} }{4+1}$

$= \frac{-2 -i+ 4i + 2(-1) }{5}$

$= \frac{-2 -i+ 4i -2 }{5}$

$= \frac{-4 +3i }{5}$

$=- \frac{4}{5} +\frac {3 }{5}i$

Compare your answer with the correct one above

Question

Define an operation $\ast$ as follows:

For all complex numbers ,

$a \ast b = \frac{ a^{3}}{b^{3} + 1}$

Evaluate $i \ast i$ .

Answer

$a \ast b = \frac{ a^{3}}{b^{3} + 1}$

$i \ast i = \frac{ i^{3}}{i^{3} + 1}$

$= \frac{ -i}{-i+ 1}$

$= \frac{ -i}{1-i }$

$= \frac{ i}{-1+i }$

Multiply the numerator and the denominator by the complex conjugate of the denominator, which is . The above becomes:

$\frac{ i\left (-1-i \right ) }{\left (-1+i \right )\left (-1-i \right ) }$

$= \frac{ -i-i^{2} }{ 1^2+i-i-i^2 }$

$=\frac{-i-i^2}{1-i^2}$

$= \frac{ -i-(-1) }{ 1+ 1 }$

$= \frac{ -i+1 }{2 }$

$= \frac{ 1-i }{2 }$

$= \frac{1}{2}- \frac{ 1}{2 }i$

Compare your answer with the correct one above

Question

Which of the following is equal to $i ^{-56}$ ?

Answer

$i ^{-56} = \frac{1}{i^{56}}$

$56 \div 4 = 14$ , so 56 is a multiple of 4. raised to the power of any multiple of 4 is equal to 1, so

$i ^{-56} = \frac{1}{i^{56}} = \frac{1}{1} = 1$ .

Compare your answer with the correct one above

Question

Multiply:

Answer

This is the product of a complex number and its complex conjugate. They can be multiplied using the pattern

$\left (A + Bi \right )\left (A - Bi \right ) = A^{2} + B^{2}$

with

$(10 + 3i)(10-3i) = 10^{2} +3^{2} = 100 + 9 = 109$

Compare your answer with the correct one above

Question

Which of the following is equal to $\left (3i \right )^{5}$ ?

Answer

By the power of a product property,

$\left (3i \right )^{5} = 3^{5} \cdot i^{5} = 3^{5} \cdot i^{4} \cdot i = 243 \cdot 1 \cdot i = 243 i$

Compare your answer with the correct one above

Question

Which of the following is equal to ?

Answer

The first step to solving this problem is distributing the exponent:

Next, we need simplify the complex portion.

$i^7=i^2\times i^2\times i^2\times i=-1\times -1\times -1\times i=-i$

Thus, our final answer is $128\times (-i)=-128i$ .

Compare your answer with the correct one above

Question

Simplify:

$\small \left ( 3 - 2i \right )\left ( 2 + i\right )$

Answer

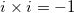Use the FOIL method that states to multiply the Firsts, Outter, Inner, Lasts. Also remember that $\small i \times i = -1$ :

$\small \left ( 3 - 2i \right )\left ( 2 + i\right )$

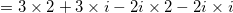
$\small = 3 \times 2 + 3 \times i - 2i \times 2 - 2i \times i$

$\small = 6 +3i -4i + 2$

$\small = 8 - i$

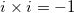
Compare your answer with the correct one above

Question

What is the eighth power of ?

Answer

$\left (3i \right )^{8}$

$= 3^{8} i^{8}$

$= 6,561 i^{8}$

raised to the power of any multiple of 4 is equal to 1, so the above expresion is equal to

$= 6,561 \cdot 1 = 6,561$

This is not among the given choices.

Compare your answer with the correct one above

Question

What is the third power of $2 + i\sqrt{5}$ ?

Answer

You are being asked to evaluate

$\left (2 + i\sqrt{5} \right )^{3}$

You can use the cube of a binomial pattern with $A = 2, B = i\sqrt{5}$ :

$\left ( A + B \right )^{3} = A^{3}+ 3A^{2}B + 3AB^{2}+ B^{3}$

$\left ( 2 + i\sqrt{5} \right )^{3} =2^{3}+ 3 \cdot 2^{2} \cdot i\sqrt{5} + 3 \cdot 2 (i\sqrt{5}) ^{2}+ (i\sqrt{5}) ^{3}$

$=8+ 3 \cdot 4 \cdot i\sqrt{5} + 6i ^{2} (\sqrt{5}) ^{2}+ i^{3}(\sqrt{5}) ^{3}$

$=8+12i\sqrt{5} + 6 (-1) 5+(-i)(5\sqrt{5})$

$=8-30 +12i\sqrt{5} -5i\sqrt{5}$

$=-22 +7i\sqrt{5}$

Compare your answer with the correct one above

Question

What is the fourth power of $3 - i\sqrt{2}$ ?

Answer

$\left (3 - i\sqrt{2} \right )^{4}$ can be calculated by squaring $3 - i\sqrt{2}$ , then squaring the result, using the square of a binomial pattern as follows:

$\left (3 - i\sqrt{2} \right )^{2}$

$=3^{2}- 2 \cdot 3 \cdot i\sqrt{2} +\left ( i\sqrt{2} \right )^{2}$

$=9- 6 i\sqrt{2} +2i^{2}$

$=9- 6 i\sqrt{2} +2(-1)$

$=7- 6 i\sqrt{2}$

$\left (3 - i\sqrt{2} \right )^{4}$

$=\left [ \left (3 - i\sqrt{2} \right )^{2} \right ]^{2}$

$=\left (7- 6 i\sqrt{2}} \right )^{2}$

$=7^{2} - 2 \cdot 7 \cdot 6 i\sqrt{2}} + \left ( 6 i\sqrt{2}} \right )^{2}$

$=49-84 i\sqrt{2}} + 6^{2} i^{2} \left ( \sqrt{2}} \right )^{2}$

$=49-84 i\sqrt{2}} +36 (-1) (2)$

$=49-84 i\sqrt{2}} -72$

$=-23-84 i\sqrt{2}}$

Compare your answer with the correct one above

Question

Multiply by its complex conjugate. What is the product?

Answer

The product of any complex number and its complex conjugate is the real number $a^{2}+b^{2}$ , so all that is needed here is to evaluate the expression:

$32^{2}+ 18 ^{2}= 1,024+ 324 = 1,348$

Compare your answer with the correct one above

Question

What is the eighth power of ?

Answer

First, square using the square of a binomial pattern as follows:

$\left (1+ i \right )^{2}$

$= 1^{2}+ 2 \cdot 1 \cdot i + i^{2}$

Raising this number to the fourth power yields the correct response:

$\left (1+ i \right )^{8}$

$= \left [\left (1+ i \right )^{2} \right ]^{4}$

$= (2i)^{4}$

$= (2 )^{4} \cdot i^{4}$

$=16 \cdot 1 = 16$

Compare your answer with the correct one above

Question

What is the ninth power of ?

Answer

$\left ( -2i\right )^{9}$

$= \left ( -2 \right )^{9} \cdot i^{9}$

To raise a negative number to an odd power, take the absolute value of the base to that power and give its opposite:

$\left ( -2\right )^{9} = - \left ( 2^{9}\right ) = -512$

To raise to a power, divide the power by 4 and raise to the remainder. Since

$9 \div 4 = 2 \textup{ R }1$ ,

$i^{9} = i^{1}= i$

Therefore,

$\left ( -2i\right )^{9}= \left ( -2 \right )^{9} \cdot i^{9} = -512 i$

Compare your answer with the correct one above

Tap the card to reveal the answer