Integers - PSAT Math
Card 0 of 20
If x represents an even integer, which of the following expressions represents an odd integer?
If x represents an even integer, which of the following expressions represents an odd integer?
Pick any even integer (2, 4, 6, etc.) to represent x. The only value that is odd is 3_x_ + 1. Any number multiplied by an even integer will be even. When an even number is added and subtracted to that product, the result will be even as well. 3_x_ + 1 is the only choice that adds an odd number to the product.
Pick any even integer (2, 4, 6, etc.) to represent x. The only value that is odd is 3_x_ + 1. Any number multiplied by an even integer will be even. When an even number is added and subtracted to that product, the result will be even as well. 3_x_ + 1 is the only choice that adds an odd number to the product.
Compare your answer with the correct one above
My sister invited me to play an online word game. In the game vowels (a,e,i,o,u) are worth 3 points and consonants are worth 5. How much would I score if I use the word “University” ?
My sister invited me to play an online word game. In the game vowels (a,e,i,o,u) are worth 3 points and consonants are worth 5. How much would I score if I use the word “University” ?
In the word we have 4 vowels (3 x 4 = 12 points) and 6 consonants (5 x 6= 30). If we add the points together we get a total of 42 points.
In the word we have 4 vowels (3 x 4 = 12 points) and 6 consonants (5 x 6= 30). If we add the points together we get a total of 42 points.
Compare your answer with the correct one above
What is the sum of multiples of 10 from 10 to 140 inclusive?
What is the sum of multiples of 10 from 10 to 140 inclusive?
Listing them all, 10-20-30-40-50-60-70-80-90-100-110-120-130-140 you see you can divide the numbers in half (7 pairs). Alternatively you can take (140-10+10)/2/10, adding that additional +10 in the numerator because it is inclusive, giving you 7. Just adding the top and bottom numbers gives you 10+140 for 150. 150*7 is 1050.
Listing them all, 10-20-30-40-50-60-70-80-90-100-110-120-130-140 you see you can divide the numbers in half (7 pairs). Alternatively you can take (140-10+10)/2/10, adding that additional +10 in the numerator because it is inclusive, giving you 7. Just adding the top and bottom numbers gives you 10+140 for 150. 150*7 is 1050.
Compare your answer with the correct one above
Suppose you know the values of the variables in the expression
and you wish to evaluate it.
Which operation do you execute last?
Suppose you know the values of the variables in the expression
and you wish to evaluate it.
Which operation do you execute last?
In the absence of grouping symbols, the first operations that should be carried out are exponentiations, followed by multiplications and divisions, followed by additions and subtractions.
The additions and subtractions are carried out from left to right. Since the addition is the one to the right, it is performed last.
In the absence of grouping symbols, the first operations that should be carried out are exponentiations, followed by multiplications and divisions, followed by additions and subtractions.
The additions and subtractions are carried out from left to right. Since the addition is the one to the right, it is performed last.
Compare your answer with the correct one above
What number replaces the circle in the following sequence?
What number replaces the circle in the following sequence?
The sequence is formed by starting with 1 and adding successive powers of 5. The numbers are obtained as follows:
- the correct response.
The sequence is formed by starting with 1 and adding successive powers of 5. The numbers are obtained as follows:
Compare your answer with the correct one above
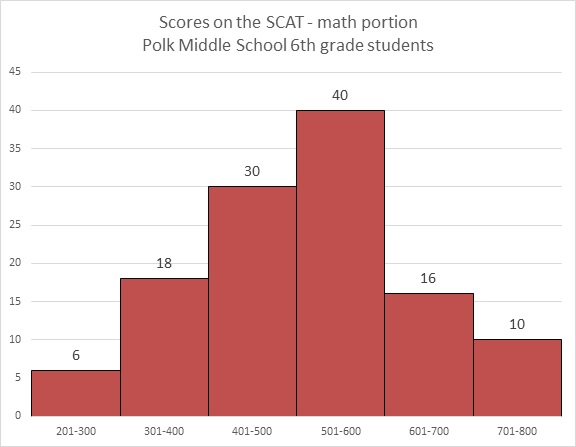
Refer to the above graph. Francie, a sixth grader at Polk, scored a 372 on the math portion of the SCAT. Which of the following could have been her rank among the students?
Refer to the above graph. Francie, a sixth grader at Polk, scored a 372 on the math portion of the SCAT. Which of the following could have been her rank among the students?
By scoring a 372, Francie was outcored by all of the students who finished in the 401-800 ranges, which add up to:
students.
She was outscored by at most an additional 17 students (the other 17 in the 301-400 range), for a total of at most
students.
Francie finished between 97th and 114th place, making 100th place the only possible choice.
By scoring a 372, Francie was outcored by all of the students who finished in the 401-800 ranges, which add up to:
She was outscored by at most an additional 17 students (the other 17 in the 301-400 range), for a total of at most
Francie finished between 97th and 114th place, making 100th place the only possible choice.
Compare your answer with the correct one above
a, b, c are integers.
abc < 0
ab > 0
bc > 0
Which of the following must be true?
a, b, c are integers.
abc < 0
ab > 0
bc > 0
Which of the following must be true?
Let's reductively consider what this data tells us.
Consider each group (a,b,c) as a group of signs.
From abc < 0, we know that the following are possible:
(–, +, +), (+, –, +), (+, +, –), (–, –, –)
From ab > 0, we know that we must eliminate (–, +, +) and (+, –, +)
From bc > 0, we know that we must eliminate (+, +, –)
Therefore, any of our answers must hold for (–, –, –)
This eliminates immediately a > 0, b > 0
Likewise, it eliminates a – b > 0 because we do not know the relative sizes of a and b. This could therefore be positive or negative.
Finally, ac is a product of negatives and is therefore positive. Hence ac < 0 does not hold.
We are left with a + b < 0, which is true, for two negatives added must be negative.
Let's reductively consider what this data tells us.
Consider each group (a,b,c) as a group of signs.
From abc < 0, we know that the following are possible:
(–, +, +), (+, –, +), (+, +, –), (–, –, –)
From ab > 0, we know that we must eliminate (–, +, +) and (+, –, +)
From bc > 0, we know that we must eliminate (+, +, –)
Therefore, any of our answers must hold for (–, –, –)
This eliminates immediately a > 0, b > 0
Likewise, it eliminates a – b > 0 because we do not know the relative sizes of a and b. This could therefore be positive or negative.
Finally, ac is a product of negatives and is therefore positive. Hence ac < 0 does not hold.
We are left with a + b < 0, which is true, for two negatives added must be negative.
Compare your answer with the correct one above
How many elements of the set 
are less than 
?
How many elements of the set
The absolute value of a negative number can be calculated by simply removing the negative symbol. Therefore,
All four (negative) numbers in the set 
are less than this positive number.
The absolute value of a negative number can be calculated by simply removing the negative symbol. Therefore,
All four (negative) numbers in the set
Compare your answer with the correct one above
The sum of three consecutive odd integers is 93. What is the largest of the integers?
The sum of three consecutive odd integers is 93. What is the largest of the integers?
Consecutive odd integers differ by 2. If the smallest integer is x, then
x + (x + 2) + (x + 4) = 93
3x + 6 = 93
3x = 87
x = 29
The three numbers are 29, 31, and 33, the largest of which is 33.
Consecutive odd integers differ by 2. If the smallest integer is x, then
x + (x + 2) + (x + 4) = 93
3x + 6 = 93
3x = 87
x = 29
The three numbers are 29, 31, and 33, the largest of which is 33.
Compare your answer with the correct one above
Which of the following could represent the sum of 3 consecutive odd integers, given that d is one of the three?
Which of the following could represent the sum of 3 consecutive odd integers, given that d is one of the three?
If the largest of the three consecutive odd integers is d, then the three numbers are (in descending order):
d, d – 2, d – 4
This is true because consecutive odd integers always differ by two. Adding the three expressions together, we see that the sum is 3_d_ – 6.
If the largest of the three consecutive odd integers is d, then the three numbers are (in descending order):
d, d – 2, d – 4
This is true because consecutive odd integers always differ by two. Adding the three expressions together, we see that the sum is 3_d_ – 6.
Compare your answer with the correct one above
, where 
and 
are distinct positive integers. Which of the following could be values of 
and 
?
Since 
and 
must be positive, eliminate choices with negative numbers or zero. Since they must be distinct (different), eliminate choices where 
. This leaves 4 and 5 (which is the only choice that does not add to 20), and the correct answer, 5 and 15.
Since
Compare your answer with the correct one above
You are given that 
are all positive integers. Also, you are given that:
is an odd number. 
can be even or odd. What is known about the odd/even status of the other four numbers?
You are given that
The odd/even status of 
is not known, so no information can be determined about that of 
.
is known to be an integer, so 
is an even integer. Added to odd number 
, an odd sum is yielded; this is 
.
is known to be odd, so 
is also odd. Added to odd number 
, an even sum is yielded; this is 
.
is known to be even, so 
is even. Added to odd number 
; an odd sum is yielded; this is 
.
The numbers known to be odd are 
and 
; the number known to be even is 
; nothing is known about 
.
The odd/even status of
The numbers known to be odd are
Compare your answer with the correct one above
You are given that 
are all positive integers. Also, you are given that:
is an odd number. 
can be even or odd. What is known about the odd/even status of the other four numbers?
You are given that
A power of an integer takes on the same odd/even status as that integer. Therefore, without knowing the odd/even status of 
, we do not know that of 
, and, subsequently, we cannot know that of 
. As a result, we cannot know the status of any of the other values of the other three variables in the subsequent statements. Therefore, none of the four choices are correct.
A power of an integer takes on the same odd/even status as that integer. Therefore, without knowing the odd/even status of
Compare your answer with the correct one above
, 
, 
, and 
are positive integers.
is odd.
Which of the following is possible?
I) Exactly two of 
are odd.
II) Exactly three of 
are odd.
III) All four of 
are odd.
Which of the following is possible?
I) Exactly two of
II) Exactly three of
III) All four of
If exactly two of 
are odd, then exactly one of the seven expressions being added is odd - namely, the only one that does not have an even factor (for example, if 
and 
are odd, then the only odd number is 
). This makes 
the sum of one odd number and six even number and, subsequently, odd.
If exactly three of 
are odd, then exactly three of the seven expressions being added are odd - namely, the three that do not include the even factor (for example, if 
, 
, and 
are odd, then the three odd numbers are 
, 
, and 
). This makes 
the sum of three odd numbers and four even numbers and, subsequently, odd.
If all four of 
are odd, then all of the seven expressions being added, being the product of only odd numbers, are odd. This makes 
the sum of seven odd numbers, and, subsequently, odd.
The correct choice is that all three scenarios are possible.
If exactly two of
If exactly three of
If all four of
The correct choice is that all three scenarios are possible.
Compare your answer with the correct one above
You are given that are all positive integers. Also, you are given that:
You are given that 
is odd, but you are not told whether 
is even or odd. What can you tell about whether the values of the other four variables are even or odd?
You are given that
You are given that
, the product of an even integer and another integer, is even. Therefore, 
is equal to the sum of an odd number 
and an even number 
, and it is odd.
, the product of odd integers, is odd, so 
, the sum of odd integers 
and 
, is even.
, the product of an odd integer and an even integer, is even, so 
, the sum of an odd integer 
and even integer 
, is odd.
, the product of odd integers, is odd, so 
, the sum of odd integers 
and 
, is even.
The correct response is that 
and 
are odd and that 
and 
are even.
The correct response is that
Compare your answer with the correct one above
Solve: 
Solve:
Add the ones digits:
Since there is no tens digit to carry over, proceed to add the tens digits:
The answer is 
.
Add the ones digits:
Since there is no tens digit to carry over, proceed to add the tens digits:
The answer is
Compare your answer with the correct one above
At a certain high school, everyone must take either Latin or Greek. There are 
more students taking Latin than there are students taking Greek. If there are 
students taking Greek, how many total students are there?
At a certain high school, everyone must take either Latin or Greek. There are
If there are 
students taking Greek, then there are 
or 
students taking Latin. However, the question asks how many total students there are in the school, so you must add these two values together to get:
or 
total students.
If there are
Compare your answer with the correct one above
If m and n are both even integers, which of the following must be true?
l. _m_2/_n_2 is even
ll. _m_2/_n_2 is odd
lll. _m_2 + _n_2 is divisible by four
If m and n are both even integers, which of the following must be true?
l. _m_2/_n_2 is even
ll. _m_2/_n_2 is odd
lll. _m_2 + _n_2 is divisible by four
While I & II can be true, examples can be found that show they are not always true (for example, 22/22 is odd and 42/22 is even).
III is always true – a square even number is always divisible by four, and the distributive property tell us that adding two numbers with a common factor gives a sum that also has that factor.
While I & II can be true, examples can be found that show they are not always true (for example, 22/22 is odd and 42/22 is even).
III is always true – a square even number is always divisible by four, and the distributive property tell us that adding two numbers with a common factor gives a sum that also has that factor.
Compare your answer with the correct one above
Let S be a set that consists entirely of even integers, and let T be the set that consists of each of the elements in S increased by two. Which of the following must be even?
I. the mean of T
II. the median of T
III. the range of T
Let S be a set that consists entirely of even integers, and let T be the set that consists of each of the elements in S increased by two. Which of the following must be even?
I. the mean of T
II. the median of T
III. the range of T
S consists of all even integers. If we were to increase each of these even numbers by 2, then we would get another set of even numbers, because adding 2 to an even number yields an even number. In other words, T also consists entirely of even numbers.
In order to find the mean of T, we would need to add up all of the elements in T and then divide by however many numbers are in T. If we were to add up all of the elements of T, we would get an even number, because adding even numbers always gives another even number. However, even though the sum of the elements in T must be even, if the number of elements in T was an even number, it's possible that dividing the sum by the number of elements of T would be an odd number.
For example, let's assume T consists of the numbers 2, 4, 6, and 8. If we were to add up all of the elements of T, we would get 20. We would then divide this by the number of elements in T, which in this case is 4. The mean of T would thus be 20/4 = 5, which is an odd number. Therefore, the mean of T doesn't have to be an even number.
Next, let's analyze the median of T. Again, let's pretend that T consists of an even number of integers. In this case, we would need to find the average of the middle two numbers, which means we would add the two numbers, which gives us an even number, and then we would divide by two, which is another even number. The average of two even numbers doesn't have to be an even number, because dividing an even number by an even number can produce an odd number.
For example, let's pretend T consists of the numbers 2, 4, 6, and 8. The median of T would thus be the average of 4 and 6. The average of 4 and 6 is (4+6)/2 = 5, which is an odd number. Therefore, the median of T doesn't have to be an even number.
Finally, let's examine the range of T. The range is the difference between the smallest and the largest numbers in T, which both must be even. If we subtract an even number from another even number, we will always get an even number. Thus, the range of T must be an even number.
Of choices I, II, and III, only III must be true.
The answer is III only.
S consists of all even integers. If we were to increase each of these even numbers by 2, then we would get another set of even numbers, because adding 2 to an even number yields an even number. In other words, T also consists entirely of even numbers.
In order to find the mean of T, we would need to add up all of the elements in T and then divide by however many numbers are in T. If we were to add up all of the elements of T, we would get an even number, because adding even numbers always gives another even number. However, even though the sum of the elements in T must be even, if the number of elements in T was an even number, it's possible that dividing the sum by the number of elements of T would be an odd number.
For example, let's assume T consists of the numbers 2, 4, 6, and 8. If we were to add up all of the elements of T, we would get 20. We would then divide this by the number of elements in T, which in this case is 4. The mean of T would thus be 20/4 = 5, which is an odd number. Therefore, the mean of T doesn't have to be an even number.
Next, let's analyze the median of T. Again, let's pretend that T consists of an even number of integers. In this case, we would need to find the average of the middle two numbers, which means we would add the two numbers, which gives us an even number, and then we would divide by two, which is another even number. The average of two even numbers doesn't have to be an even number, because dividing an even number by an even number can produce an odd number.
For example, let's pretend T consists of the numbers 2, 4, 6, and 8. The median of T would thus be the average of 4 and 6. The average of 4 and 6 is (4+6)/2 = 5, which is an odd number. Therefore, the median of T doesn't have to be an even number.
Finally, let's examine the range of T. The range is the difference between the smallest and the largest numbers in T, which both must be even. If we subtract an even number from another even number, we will always get an even number. Thus, the range of T must be an even number.
Of choices I, II, and III, only III must be true.
The answer is III only.
Compare your answer with the correct one above
Kacey works 5 hours per day on Monday, Tuesday, and Wednesday, as well as 9 hours on Thursday and Friday. She does not work on Saturday or Sunday. Her total earnings per week is $363. How much does she earn per hour in dollars?
Kacey works 5 hours per day on Monday, Tuesday, and Wednesday, as well as 9 hours on Thursday and Friday. She does not work on Saturday or Sunday. Her total earnings per week is $363. How much does she earn per hour in dollars?
Kacey works 5 hours a day for 3 days and 9 hours a day for 2 days. (5)(3) = 15 and (2)(9) = 18. 15 + 18 = 33 hours worked a week. $363/33 hours = $11/hr.
Kacey works 5 hours a day for 3 days and 9 hours a day for 2 days. (5)(3) = 15 and (2)(9) = 18. 15 + 18 = 33 hours worked a week. $363/33 hours = $11/hr.
Compare your answer with the correct one above