Expressions - PSAT Math
Card 0 of 20
Simplify the following rational expression: (9x - 2)/(x2) MINUS (6x - 8)/(x2)
Simplify the following rational expression: (9x - 2)/(x2) MINUS (6x - 8)/(x2)
Since both expressions have a common denominator, x2, we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.
Since both expressions have a common denominator, x2, we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.
Compare your answer with the correct one above
Simplify.
Simplify.
Same denominator means you add straight across the numerators, keeping the denominator the same.
Add like terms.
Final Answer.
Same denominator means you add straight across the numerators, keeping the denominator the same.
Add like terms.
Final Answer.
Compare your answer with the correct one above
Simplify.
Simplify.
Check for same Denominator
Add like terms
Check for GCF or if the expression can be factored
After factoring, divide out like terms. 
Final Answer
Check for same Denominator
Add like terms
Check for GCF or if the expression can be factored
After factoring, divide out like terms.
Final Answer
Compare your answer with the correct one above
Simplify the expression.
Simplify the expression.
To add rational expressions, first find the least common denominator. Because the denominator of the first fraction factors to 2(x+2), it is clear that this is the common denominator. Therefore, multiply the numerator and denominator of the second fraction by 2.
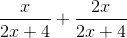
This is the most simplified version of the rational expression.
To add rational expressions, first find the least common denominator. Because the denominator of the first fraction factors to 2(x+2), it is clear that this is the common denominator. Therefore, multiply the numerator and denominator of the second fraction by 2.
This is the most simplified version of the rational expression.
Compare your answer with the correct one above
Which of the following is equivalent to 
? Assume that denominators are always nonzero.
Which of the following is equivalent to
We will need to simplify the expression 
. We can think of this as a large fraction with a numerator of 
and a denominator of 
.
In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. 
has a denominator of 
, and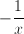 
has a denominator of 
. The least common denominator that these two fractions have in common is 
. Thus, we are going to write equivalent fractions with denominators of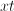 
.
In order to convert the fraction 
to a denominator with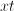 
, we will need to multiply the top and bottom by 
.
Similarly, we will multiply the top and bottom of 
by 
.
We can now rewrite 
as follows:
= 
Let's go back to the original fraction 
. We will now rewrite the numerator:
= 
To simplify this further, we can think of 
as the same as 
. When we divide a fraction by another quantity, this is the same as multiplying the fraction by the reciprocal of that quantity. In other words, 
.
= 
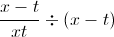Lastly, we will use the property of exponents which states that, in general, 
.
The answer is 
.
We will need to simplify the expression
In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator.
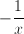
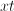
In order to convert the fraction
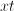
Similarly, we will multiply the top and bottom of
We can now rewrite
Let's go back to the original fraction
To simplify this further, we can think of
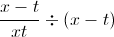
Lastly, we will use the property of exponents which states that, in general,
The answer is
Compare your answer with the correct one above
Twenty percent of a number, 
, is four greater than the product of that number and six. Which of the following algebraic equations could be used to find 
?
Twenty percent of a number,
The "is" in the question means "equal," so whatever comes before "is" must be equal to whatever comes after. We will find an expression for the information before "is" and an expression for the information after "is," and then we will set these two expressions equal.
Twenty percent of a number can be represented as 0.2n, because 20% expressed as a decimal is 0.2, and because twenty percent "of" a number means the product of that number and twenty percent.
Four greater than the product of a number and six means that we must first find the product of that number and six, and then increase this value by 4.
The product of a number and six means that we must multiply this number by six, which can be represented by 6n. Increasing 6n by 4 can be modeled by the expression 6n + 4, or 4 + 6n (because of the commutative property of addition).
Setting the two expressions equal gives us 0.2n = 4 + 6n .
The "is" in the question means "equal," so whatever comes before "is" must be equal to whatever comes after. We will find an expression for the information before "is" and an expression for the information after "is," and then we will set these two expressions equal.
Twenty percent of a number can be represented as 0.2n, because 20% expressed as a decimal is 0.2, and because twenty percent "of" a number means the product of that number and twenty percent.
Four greater than the product of a number and six means that we must first find the product of that number and six, and then increase this value by 4.
The product of a number and six means that we must multiply this number by six, which can be represented by 6n. Increasing 6n by 4 can be modeled by the expression 6n + 4, or 4 + 6n (because of the commutative property of addition).
Setting the two expressions equal gives us 0.2n = 4 + 6n .
Compare your answer with the correct one above
An elementary school class consists of 
boys and 
girls. What fraction of the class is female?
An elementary school class consists of
There are B+G total students in the elementary school class, so G out of B+G are girls.
There are B+G total students in the elementary school class, so G out of B+G are girls.
Compare your answer with the correct one above
A total of 150 million votes were tallied in a presidential election. Votes were cast for either Hillary Clinton, Rand Paul, Al Gore, or Gary Johnson. If Clinton received 3 times the number of votes as Johnson, Paul received 30% of the vote, and Gore receieved 30 million total votes, who received the most votes in the election?
A total of 150 million votes were tallied in a presidential election. Votes were cast for either Hillary Clinton, Rand Paul, Al Gore, or Gary Johnson. If Clinton received 3 times the number of votes as Johnson, Paul received 30% of the vote, and Gore receieved 30 million total votes, who received the most votes in the election?
There are a few ways to do this problem, but we will focus on the total number of votes method as follows. First, let Clinton = C, Gore = G, Paul = P, and Johnson = J. We know C + G + P + J = 150 million. We also know that C = 3J. Paul received 30% of the vote which is 150,000,000 * .3 = 45 million votes. Gore received 30 million votes. We can now create an equation with individual totals and substitute 3J for Clinton's vote total:
3J + 30 million + 45 million + J = 150 million
4J = 75 million
J = 18.75 million
Then C = 3J = 56.25 million. So Clinton received 56.25 million votes, Paul received 45 million votes, Gore received 30 million votes, and Johnson received 18.75 million votes. The correct answer is Hillary Clinton.
There are a few ways to do this problem, but we will focus on the total number of votes method as follows. First, let Clinton = C, Gore = G, Paul = P, and Johnson = J. We know C + G + P + J = 150 million. We also know that C = 3J. Paul received 30% of the vote which is 150,000,000 * .3 = 45 million votes. Gore received 30 million votes. We can now create an equation with individual totals and substitute 3J for Clinton's vote total:
3J + 30 million + 45 million + J = 150 million
4J = 75 million
J = 18.75 million
Then C = 3J = 56.25 million. So Clinton received 56.25 million votes, Paul received 45 million votes, Gore received 30 million votes, and Johnson received 18.75 million votes. The correct answer is Hillary Clinton.
Compare your answer with the correct one above
Based on the chart, which equation represents the table data?
Based on the chart, which equation represents the table data?
| | | | |
|---|---|---|---|---|
| | | | |
The easiest way to solve this problem is to guess-and-check the answer choices. The equation that can be used to match the table will be correct.
We can see that the values in the table match the equation 
for each given value. Thus, this must be our answer.
We can also determine certain characteristics from the table itself. For example, as x increases, y(x) decreases. This tells us that there is likely a negative coefficient, which can help narrow down the answer options.
The easiest way to solve this problem is to guess-and-check the answer choices. The equation that can be used to match the table will be correct.
We can see that the values in the table match the equation
We can also determine certain characteristics from the table itself. For example, as x increases, y(x) decreases. This tells us that there is likely a negative coefficient, which can help narrow down the answer options.
Compare your answer with the correct one above
Justin makes 61.9% of his free throws. During the season he had 84 free throw attempts. How many of Jason’s shots did not go in?
Justin makes 61.9% of his free throws. During the season he had 84 free throw attempts. How many of Jason’s shots did not go in?
Find how many free throws Justin made: 84 x 0.619 = 51.99. Since the problem talks free throws, we round to 52 shots went in. To calculate shots missed:
84 – 52 = 32.
Find how many free throws Justin made: 84 x 0.619 = 51.99. Since the problem talks free throws, we round to 52 shots went in. To calculate shots missed:
84 – 52 = 32.
Compare your answer with the correct one above
If 5x + 30 = 6 – 7x, then x = ?
If 5x + 30 = 6 – 7x, then x = ?
Combine like terms by subtracting 6 from both sides so: 5x + 24 = –7x. Then subtract 5x from both sides: 24 = –12x. Divide both sides by –12 and x = –2.
Combine like terms by subtracting 6 from both sides so: 5x + 24 = –7x. Then subtract 5x from both sides: 24 = –12x. Divide both sides by –12 and x = –2.
Compare your answer with the correct one above
If ab - bc + d = d2 - c2, then what is the value of a when b is two, c is negative one, and d is zero?
If ab - bc + d = d2 - c2, then what is the value of a when b is two, c is negative one, and d is zero?
ab - bc + d = d2 - c2
We need to substitute values in for b, c, and d, and then solve the equation for a.
a(2) - 2(-1) + 0 = 02 - (-1)2
2a +2 + 0 = 0 - (1)
2a + 2 = -1
2a = -3
a = -3/2
The answer is -3/2.
ab - bc + d = d2 - c2
We need to substitute values in for b, c, and d, and then solve the equation for a.
a(2) - 2(-1) + 0 = 02 - (-1)2
2a +2 + 0 = 0 - (1)
2a + 2 = -1
2a = -3
a = -3/2
The answer is -3/2.
Compare your answer with the correct one above
If 11x + 4 = 19x – 12, then what is 2x – 4?
If 11x + 4 = 19x – 12, then what is 2x – 4?
First solve for x. The first equation would simplify as:
16 = 8x
x = 2
If we plug x = 2 into the second expression:
2(2) – 4 = 0
0 is the correct answer.
First solve for x. The first equation would simplify as:
16 = 8x
x = 2
If we plug x = 2 into the second expression:
2(2) – 4 = 0
0 is the correct answer.
Compare your answer with the correct one above
If x = 2 and y = 3, then evaluate 2(x – 3) + 5y2
If x = 2 and y = 3, then evaluate 2(x – 3) + 5y2
To evaluate an expression we make substitutions into the expression
2(x – 3) + 5y2 becomes 2(2 – 3) + 5 * 32 = –2 + 45 = 43
To evaluate an expression we make substitutions into the expression
2(x – 3) + 5y2 becomes 2(2 – 3) + 5 * 32 = –2 + 45 = 43
Compare your answer with the correct one above
IF 5x3 = 40, then what is the value of 12x – (x/2)?
IF 5x3 = 40, then what is the value of 12x – (x/2)?
Use the first equation to solve for x, then plug into the 2nd equation to find a value.
5x3 = 40
x3 = 8
x = 2
12(2) – (2/2) = 24 – 1 = 23
Use the first equation to solve for x, then plug into the 2nd equation to find a value.
5x3 = 40
x3 = 8
x = 2
12(2) – (2/2) = 24 – 1 = 23
Compare your answer with the correct one above
A rowing team paddles upstream at a rate of 10 miles every 2 hours and downstream at a rate of 27 miles every 3 hours. Assuming they are paddling at the same rate up and downstream, what is the speed of the water?
A rowing team paddles upstream at a rate of 10 miles every 2 hours and downstream at a rate of 27 miles every 3 hours. Assuming they are paddling at the same rate up and downstream, what is the speed of the water?
Upstream: p – w = (10/2) or p – w = 5 miles/hour
Downstream: p + w = (27/3) or p + w = 9 miles/hour
Then we add the two equations together to cancel out the w's. After adding we see
2p = 14
p = 7 miles/hour where p is the rate of the paddling. We plug p into the equation to find
w = 2 miles/hour where w is the rate of the stream's water.
Upstream: p – w = (10/2) or p – w = 5 miles/hour
Downstream: p + w = (27/3) or p + w = 9 miles/hour
Then we add the two equations together to cancel out the w's. After adding we see
2p = 14
p = 7 miles/hour where p is the rate of the paddling. We plug p into the equation to find
w = 2 miles/hour where w is the rate of the stream's water.
Compare your answer with the correct one above
Tim is two years older than his twin sisters, Rachel and Claire. The sum of their ages is 65. How old is Tim?
Tim is two years older than his twin sisters, Rachel and Claire. The sum of their ages is 65. How old is Tim?
The answer is 23.
Since Rachel and Claire are twins they are the same age. We will use the variable r to represent both Rachel and Claire's ages.
From the question we can form two equations. They are:
t = r + 2 and 65 = t + 2r
lets plug the first equation into the second to solve for r.
65 = (r + 2) + 2r
65 = 3r +2
63 = 3r
r = 21 This means Rachel and Claire are 21 years old. Plug this into the equation so
t = 23 Tim is 23 years old.
The answer is 23.
Since Rachel and Claire are twins they are the same age. We will use the variable r to represent both Rachel and Claire's ages.
From the question we can form two equations. They are:
t = r + 2 and 65 = t + 2r
lets plug the first equation into the second to solve for r.
65 = (r + 2) + 2r
65 = 3r +2
63 = 3r
r = 21 This means Rachel and Claire are 21 years old. Plug this into the equation so
t = 23 Tim is 23 years old.
Compare your answer with the correct one above
Drink A is 20% water by weight, and drink B is 35% water by weight. How many fluid ounces of drink A must be added to 80 oz of drink B to have a drink whose final proportion of water is 30%?
Drink A is 20% water by weight, and drink B is 35% water by weight. How many fluid ounces of drink A must be added to 80 oz of drink B to have a drink whose final proportion of water is 30%?
It's easiest if we convert all percentages to actual oz of water for each step here. As such, 35% of the 80 oz of drink B would have 0.35(80) = 28 oz of water in it.
We can set up an equation that similarly converts each "percentage of a fixed weight of liquid" to ensure that our final weight is equivalent to 30% to the sum of drink A and B. On the left side, the fixed values are the percentages of each drink individually, and on the right side is what the question requires as a fixed percentage of the final weight:
0.2(A) + 0.35(80) = 0.3(A + 80)
0.2A + 28 = 0.3A + 24
A = 40
Solving for A, we get 40 oz of A that must be poured into B. You may plug this back into the equation to check it.
It's easiest if we convert all percentages to actual oz of water for each step here. As such, 35% of the 80 oz of drink B would have 0.35(80) = 28 oz of water in it.
We can set up an equation that similarly converts each "percentage of a fixed weight of liquid" to ensure that our final weight is equivalent to 30% to the sum of drink A and B. On the left side, the fixed values are the percentages of each drink individually, and on the right side is what the question requires as a fixed percentage of the final weight:
0.2(A) + 0.35(80) = 0.3(A + 80)
0.2A + 28 = 0.3A + 24
A = 40
Solving for A, we get 40 oz of A that must be poured into B. You may plug this back into the equation to check it.
Compare your answer with the correct one above
Let x&y = xy – x + y. Which of the following is equal to 5&3 ?
Let x&y = xy – x + y. Which of the following is equal to 5&3 ?
First, we need to evaluate 5&3.
Since x&y = xy – x + y, we can find 5&3 as follows:
5&3 = 5(3) – 5 + 3
= 15 – 5 + 3
= 13
Now, we need to go through each of the choices and determine which one equals 13.
Let's start with 2&(8&1). Remember that we must first evaluate inside the parantheses.
2&(8&1) = 2&(8(1) – 8 + 1)
= 2&(8 – 8 + 1)
= 2&(1)
= 2(1) – 2 + 1 = 1, which doesn't equal 13.
Next, let's evaluate 4&(3&4).
4&(3&4) = 4&(3(4) – 3 + 4)
= 4&(13) = 4(13) – 4 + 13 = 61.
Next, we can evaulate 8&(2&0).
8&(2&0) = 8&(2(0) – 2 + 0)
= 8&(–2) = 8(–2) – 8 + 2 = –22.
Next, let's find 3&(5&2).
3&(5&2) = 3&(5(2) – 5 + 2)
= 3&(7) = 3(7) – 3 + 7 = 25.
Finally, lets evaluate 11&(0&2).
11&(0&2) = 11&(0(2) – 0 + 2)
= 11&(2) = 11(2) – 11 + 2 = 13.
The answer is 11&(0&2).
First, we need to evaluate 5&3.
Since x&y = xy – x + y, we can find 5&3 as follows:
5&3 = 5(3) – 5 + 3
= 15 – 5 + 3
= 13
Now, we need to go through each of the choices and determine which one equals 13.
Let's start with 2&(8&1). Remember that we must first evaluate inside the parantheses.
2&(8&1) = 2&(8(1) – 8 + 1)
= 2&(8 – 8 + 1)
= 2&(1)
= 2(1) – 2 + 1 = 1, which doesn't equal 13.
Next, let's evaluate 4&(3&4).
4&(3&4) = 4&(3(4) – 3 + 4)
= 4&(13) = 4(13) – 4 + 13 = 61.
Next, we can evaulate 8&(2&0).
8&(2&0) = 8&(2(0) – 2 + 0)
= 8&(–2) = 8(–2) – 8 + 2 = –22.
Next, let's find 3&(5&2).
3&(5&2) = 3&(5(2) – 5 + 2)
= 3&(7) = 3(7) – 3 + 7 = 25.
Finally, lets evaluate 11&(0&2).
11&(0&2) = 11&(0(2) – 0 + 2)
= 11&(2) = 11(2) – 11 + 2 = 13.
The answer is 11&(0&2).
Compare your answer with the correct one above
x is 75% of y, which is 8 times the amount of 150% of z. What is x in terms of z?
x is 75% of y, which is 8 times the amount of 150% of z. What is x in terms of z?
Just take this step by step. First write out each equation:
x = 0.75y
y = 8(1.5z)
First, simplify the second equation:
y = 12z
Then, substitute y from this equation into the first:
x = 0.75(12z) = 9z
Just take this step by step. First write out each equation:
x = 0.75y
y = 8(1.5z)
First, simplify the second equation:
y = 12z
Then, substitute y from this equation into the first:
x = 0.75(12z) = 9z
Compare your answer with the correct one above