Law of Cosines and Sines - Pre-Calculus
Card 0 of 20
Use the Law of Cosines to find  .
.

(Triangle not drawn to scale.)
Use the Law of Cosines to find 

(Triangle not drawn to scale.)
We need to use the Law of Cosines in order to solve this problem

in this case, 
In order to arrive at our answer, we plug the numbers into our formula:



Note: we use the "approximately" to indicate the answer is around 6.6. It will vary depending on your rounding.
We need to use the Law of Cosines in order to solve this problem
in this case,
In order to arrive at our answer, we plug the numbers into our formula:
Note: we use the "approximately" to indicate the answer is around 6.6. It will vary depending on your rounding.
Compare your answer with the correct one above
Use the Law of Cosines to find  .
.

(Triangle not drawn to scale.)
Use the Law of Cosines to find 

(Triangle not drawn to scale.)
In order to solve this problem, we need to use the following formula

in this case, 
We plug our numbers into our formula and get our answer:




Note: we use the "approximately" to indicate that the answer is around 9.6. It will vary depending on your rounding.
In order to solve this problem, we need to use the following formula
in this case,
We plug our numbers into our formula and get our answer:
Note: we use the "approximately" to indicate that the answer is around 9.6. It will vary depending on your rounding.
Compare your answer with the correct one above
Which is NOT an angle of the following triangle?

(Not drawn to scale.)
Which is NOT an angle of the following triangle?

(Not drawn to scale.)
In order to solve this problem, we need to find the angles of the triangle. Only then will we be able to find which answer choice is NOT an angle. Using the Law of Cosines we are able to find each angle.






To find angle  we use the formula again or we can remember that the angles in a triangle add up to
we use the formula again or we can remember that the angles in a triangle add up to  .
.

The answer choice that isn't an actual angle of the triangle is  .
.
In order to solve this problem, we need to find the angles of the triangle. Only then will we be able to find which answer choice is NOT an angle. Using the Law of Cosines we are able to find each angle.
To find angle 

The answer choice that isn't an actual angle of the triangle is 
Compare your answer with the correct one above
Use the Law of Sines to find  in the following triangle.
in the following triangle.
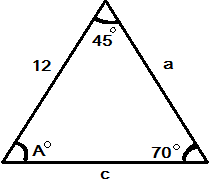
(Not drawn to scale.)
Use the Law of Sines to find 

(Not drawn to scale.)
We use the Law of Sines to solve this problem

we plug in 

solving for  we get:
we get:

We use the Law of Sines to solve this problem
we plug in
solving for 
Compare your answer with the correct one above
Use the Law of Sines to find  .
.

(Not drawn to scale.)
Use the Law of Sines to find 

(Not drawn to scale.)
We use the Law of Sines to solve this problem:

where 
We plug in the values that we will need:

Notice that we did not use  .
.
Solve for  we get:
we get:

We use the Law of Sines to solve this problem:
where
We plug in the values that we will need:
Notice that we did not use 
Solve for 
Compare your answer with the correct one above
Which of the following are the missing sides of the triangle?





Which of the following are the missing sides of the triangle?

In order to solve this problem, we need to find  . We do so by remembering the sum of the angles in a triangle is
. We do so by remembering the sum of the angles in a triangle is  :
:

We can now use the Law of Sines to find the missing sides.

 which is II.
which is II.

 which is III.
which is III.
Our answers are then II and III
In order to solve this problem, we need to find 

We can now use the Law of Sines to find the missing sides.


Our answers are then II and III
Compare your answer with the correct one above
Which of the following are the missing sides of the triangle?





Which of the following are the missing sides of the triangle?

In order to solve this problem, we need to find 
Since all the angles of a triangle add to  , we can easily find it:
, we can easily find it:

We can now use the Law of Sines to find the missing sides:

 which is I.
which is I.

 which is III.
which is III.
Our answers are then I and III.
In order to solve this problem, we need to find
Since all the angles of a triangle add to 
We can now use the Law of Sines to find the missing sides:


Our answers are then I and III.
Compare your answer with the correct one above
Solve the triangle

Solve the triangle

Since we are given all 3 sides, we can use the Law of Cosines in the angle form:



Let's start by finding angle A:


Now let's solve for B:


We can solve for C the same way, but since we now have A and B, we can use our knowledge that all interior angles of a triangle must add up to 180 to find C.

Since we are given all 3 sides, we can use the Law of Cosines in the angle form:
Let's start by finding angle A:
Now let's solve for B:
We can solve for C the same way, but since we now have A and B, we can use our knowledge that all interior angles of a triangle must add up to 180 to find C.
Compare your answer with the correct one above
Solve the triangle using the Law of Sines:

Solve the triangle using the Law of Sines:

First we need to know what the Law of Sines is:

Looking at the triangle, we know c, C, and B. We can either solve for side b, using the law, or angle A using our knowledge that the interior angles of a triangle must add up to be 180.



Now all that's left is to find side a:


First we need to know what the Law of Sines is:
Looking at the triangle, we know c, C, and B. We can either solve for side b, using the law, or angle A using our knowledge that the interior angles of a triangle must add up to be 180.
Now all that's left is to find side a:
Compare your answer with the correct one above
Given three sides of the triangle below, determine the angles  ,
,  , and
, and  in degrees.
in degrees.

Given three sides of the triangle below, determine the angles 



We are only given sides, so we must use the Law of Cosines. The equation for the Law of Cosines is
 ,
,
where  ,
,  and
and  are the sides of a triangle and the angle
are the sides of a triangle and the angle  is opposite the side
is opposite the side  .
.
We have three known sides and three unknown angles, so we must write the Law three times, where each equation lets us solve for a different angle.
To solve for angle  , we write
, we write
 and solve for
and solve for  using the inverse cosine function
using the inverse cosine function  on a calculator to get
on a calculator to get
 .
.
Similarly, for angle  ,
,


and for  ,
,

and 
We are only given sides, so we must use the Law of Cosines. The equation for the Law of Cosines is

where 




We have three known sides and three unknown angles, so we must write the Law three times, where each equation lets us solve for a different angle.
To solve for angle 




Similarly, for angle 
and for 
and
Compare your answer with the correct one above
The 2 sides of a triangle have lengths of 10 and 20. The included angle is 25 degrees. What is the length of the third side to the nearest integer?
The 2 sides of a triangle have lengths of 10 and 20. The included angle is 25 degrees. What is the length of the third side to the nearest integer?
Write the formula for the Law of Cosines.

Substitute the side lengths of the triangle and the included angle to find the third length.





Round this to the nearest integer.

Write the formula for the Law of Cosines.
Substitute the side lengths of the triangle and the included angle to find the third length.
Round this to the nearest integer.
Compare your answer with the correct one above
What is the approximate length of the unknown side of the triangle if two sides of the triangle are  and
and  , with an included angle of
, with an included angle of  ?
?
What is the approximate length of the unknown side of the triangle if two sides of the triangle are 


Write the formula for the Law of Cosines.

Substitute the known values and solve for  .
.




Write the formula for the Law of Cosines.
Substitute the known values and solve for 
Compare your answer with the correct one above

What is the measurement of side  using the Law of Cosines? Round to the nearest tenth.
using the Law of Cosines? Round to the nearest tenth.

What is the measurement of side 
The Law of Cosines for side  is,
is,
 .
.
Plugging in the information we know, the formula is,
 .
.
Then take the square of both sides:  .
.
Finally, round to the appropriate units:  .
.
The Law of Cosines for side 

Plugging in the information we know, the formula is,

Then take the square of both sides: 
Finally, round to the appropriate units: 
Compare your answer with the correct one above

What is the measurement of  ? Round to the nearest tenth, if needed.
? Round to the nearest tenth, if needed.

What is the measurement of 
We need to use the Law of Cosines for side  then solve for
then solve for  .
.
Therefore,
 .
.
Plugging in the information provided, we have:
 .
.
Then simplify,  .
.
To solve for  , use
, use  .
.
Solve and then round to the appropriate units:  . Therefore,
. Therefore,  .
.
We need to use the Law of Cosines for side 

Therefore,

Plugging in the information provided, we have:

Then simplify, 
To solve for 

Solve and then round to the appropriate units: 

Compare your answer with the correct one above

Given  and
and  , what is the measurement of
, what is the measurement of  to the nearest degree?
to the nearest degree?

Given 


Using the information we have, we can solve for  :
:
 .
.
Plugging in what we know, we have:
 .
.
Then, solve for  :
:
 .
.
Simplify, then solve for  :
:  which means
which means  .
.
Therefore, after rounding to the nearest degree,  .
.
To solve for  , subtract
, subtract  and
and  from
from  :
:  .
.
Therefore,  .
.
Using the information we have, we can solve for 

Plugging in what we know, we have:

Then, solve for 

Simplify, then solve for 


Therefore, after rounding to the nearest degree, 
To solve for 




Therefore, 
Compare your answer with the correct one above
What is the largest possible angle, measured in degrees, in triangle  if
if  ,
,  , and
, and  ?
?
What is the largest possible angle, measured in degrees, in triangle 



In the ambiguous SSA case, use Law of Sines to solve for the angle opposite the given side.

If  , then
, then  .
.
However! Another possible value of C is  .
.
In this case the angles will be  .
.
This is bigger than  and is consequently the answer.
and is consequently the answer.
In the ambiguous SSA case, use Law of Sines to solve for the angle opposite the given side.
If 

However! Another possible value of C is 
In this case the angles will be 
This is bigger than 
Compare your answer with the correct one above
Find the measure, in degrees, of the largest angle in a triangle whose sides measure  ,
,  , and
, and  .
.
Find the measure, in degrees, of the largest angle in a triangle whose sides measure 


When all three sides are given, Law of Cosines is appropriate.
Since 10 is the largest side length, it is opposite the largest angle and thus should be the c-value in the equation below.

When all three sides are given, Law of Cosines is appropriate.
Since 10 is the largest side length, it is opposite the largest angle and thus should be the c-value in the equation below.
Compare your answer with the correct one above
Find the length of the missing side,  .
.

Find the length of the missing side, 

First, use the Law of Sines to find the measurement of angle 




Recall that all the angles in a triangle need to add up to  degrees.
degrees.


Now, use the Law of Sines again to find the length of  .
.



First, use the Law of Sines to find the measurement of angle
Recall that all the angles in a triangle need to add up to 
Now, use the Law of Sines again to find the length of 
Compare your answer with the correct one above
Find the length of the missing side,  .
.

Find the length of the missing side, 

First, use the Law of Sines to find the measurement of angle 




Recall that all the angles in a triangle need to add up to  degrees.
degrees.


Now, use the Law of Sines again to find the length of  .
.



First, use the Law of Sines to find the measurement of angle
Recall that all the angles in a triangle need to add up to 
Now, use the Law of Sines again to find the length of 
Compare your answer with the correct one above
Find the length of the missing side,  .
.

Find the length of the missing side, 

First, use the Law of Sines to find the measurement of angle 




Recall that all the angles in a triangle need to add up to  degrees.
degrees.


Now, use the Law of Sines again to find the length of  .
.



First, use the Law of Sines to find the measurement of angle
Recall that all the angles in a triangle need to add up to 
Now, use the Law of Sines again to find the length of 
Compare your answer with the correct one above