Graphs of Polynomial Functions - Pre-Calculus
Card 0 of 13
Give the  -intercept of the graph of the function
-intercept of the graph of the function

Round to the nearest tenth, if applicable.
Give the 
Round to the nearest tenth, if applicable.
The  -intercept is
-intercept is  , where
, where  :
:











The  -intercept is
-intercept is  .
.
The 


The 

Compare your answer with the correct one above
Which of the following is an accurate graph of  ?
?
Which of the following is an accurate graph of 
 is a parabola, because of the general
is a parabola, because of the general  structure. The parabola opens downward because
structure. The parabola opens downward because  .
.
Solving  tells the x-value of the x-axis intercept;
tells the x-value of the x-axis intercept;




The resulting x-axis intercept is:  .
.
Setting  tells the y-value of the y-axis intercept;
tells the y-value of the y-axis intercept;




The resulting y-axis intercept is: 



Solving 
The resulting x-axis intercept is: 
Setting 
The resulting y-axis intercept is:
Compare your answer with the correct one above
Graph the following function and identify the zeros.

Graph the following function and identify the zeros.
This question tests one's ability to graph a polynomial function.
For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Use algebraic technique to factor the function.

Separating the function into two parts...

Factoring a negative one from the second set results in...

Factoring out  from the first set results in...
from the first set results in...

The new factored form of the function is,
 .
.
Now, recognize that the first binomial is a perfect square for which the following formula can be used

since

thus the simplified, factored form is,
 .
.
Step 2: Identify the roots of the function.
To find the roots of a function set its factored form equal to zero and solve for the possible x values.

Step 3: Create a table of  pairs.
pairs.

The values in the table are found by substituting in the x values into the function as follows.

Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.

This question tests one's ability to graph a polynomial function.
For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Use algebraic technique to factor the function.
Separating the function into two parts...
Factoring a negative one from the second set results in...
Factoring out 
The new factored form of the function is,

Now, recognize that the first binomial is a perfect square for which the following formula can be used
since
thus the simplified, factored form is,

Step 2: Identify the roots of the function.
To find the roots of a function set its factored form equal to zero and solve for the possible x values.
Step 3: Create a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.

Compare your answer with the correct one above
Graph the function and identify its roots.

Graph the function and identify its roots.
This question tests one's ability to graph a polynomial function.
For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Use algebraic technique to factor the function.
Recognize that the binomial is a perfect square for which the following formula can be used

since

thus the simplified, factored form is,
 .
.
Step 2: Identify the roots of the function.
To find the roots of a function set its factored form equal to zero and solve for the possible x values.


Step 3: Create a table of  pairs.
pairs.

The values in the table are found by substituting in the x values into the function as follows.

Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.

This question tests one's ability to graph a polynomial function.
For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Use algebraic technique to factor the function.
Recognize that the binomial is a perfect square for which the following formula can be used
since
thus the simplified, factored form is,

Step 2: Identify the roots of the function.
To find the roots of a function set its factored form equal to zero and solve for the possible x values.

Step 3: Create a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.

Compare your answer with the correct one above
Graph the function and identify its roots.

Graph the function and identify its roots.
This question tests one's ability to graph a polynomial function.
For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Use algebraic technique to factor the function.
Recognize that the binomial is a perfect square for which the following formula can be used

since

thus the simplified, factored form is,
 .
.
Step 2: Identify the roots of the function.
To find the roots of a function set its factored form equal to zero and solve for the possible x values.


Step 3: Create a table of  pairs.
pairs.

The values in the table are found by substituting in the x values into the function as follows.

Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.

This question tests one's ability to graph a polynomial function.
For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Use algebraic technique to factor the function.
Recognize that the binomial is a perfect square for which the following formula can be used
since
thus the simplified, factored form is,

Step 2: Identify the roots of the function.
To find the roots of a function set its factored form equal to zero and solve for the possible x values.

Step 3: Create a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.

Compare your answer with the correct one above
Graph the function and identify the roots.

Graph the function and identify the roots.
This question tests one's ability to graph a polynomial function.
For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Use algebraic technique to factor the function.
Recognize that the binomial is a perfect square for which the following formula can be used

since

thus the simplified, factored form is,
 .
.
Step 2: Identify the roots of the function.
To find the roots of a function set its factored form equal to zero and solve for the possible x values.


Step 3: Create a table of  pairs.
pairs.

The values in the table are found by substituting in the x values into the function as follows.

Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.

This question tests one's ability to graph a polynomial function.
For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Use algebraic technique to factor the function.
Recognize that the binomial is a perfect square for which the following formula can be used
since
thus the simplified, factored form is,

Step 2: Identify the roots of the function.
To find the roots of a function set its factored form equal to zero and solve for the possible x values.

Step 3: Create a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.

Compare your answer with the correct one above
Write the quadratic function for the graph:

Write the quadratic function for the graph:

Method 1:
The x-intercepts are  . These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.
. These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.
For  ,
,  . For
. For  ,
,  . These equations determine the resulting factors and the resulting function;
. These equations determine the resulting factors and the resulting function;  .
.
Multiplying the factors and simplifying,
 .
.
Answer:  .
.
Method 2:
Use the form  , where
, where  is the vertex.
is the vertex.
 is
is  , so
, so  ,
,  .
.
![(x - [-4])^{2} + (-4) = (x + 4)^{2} - 4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/478227/gif.latex)
Answer: 



Method 1:
The x-intercepts are 
For 




Multiplying the factors and simplifying,

Answer: 
Method 2:
Use the form 





Answer:
Compare your answer with the correct one above
Write the quadratic function for the graph:

Write the quadratic function for the graph:

Because there are no x-intercepts, use the form  , where vertex
, where vertex  is
is  , so
, so  ,
,  , which gives
, which gives





Because there are no x-intercepts, use the form 




Compare your answer with the correct one above
Which could be the equation for this graph?

Which could be the equation for this graph?
This graph has zeros at 3, -2, and -4.5. This means that  ,
,  , and
, and  . That last root is easier to work with if we consider it as
. That last root is easier to work with if we consider it as  and simplify it to
and simplify it to  . Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.
. Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.
Our equation results from multiplying  , which results in
, which results in  .
.
This graph has zeros at 3, -2, and -4.5. This means that 




Our equation results from multiplying 

Compare your answer with the correct one above
Write the equation for the polynomial in this graph:
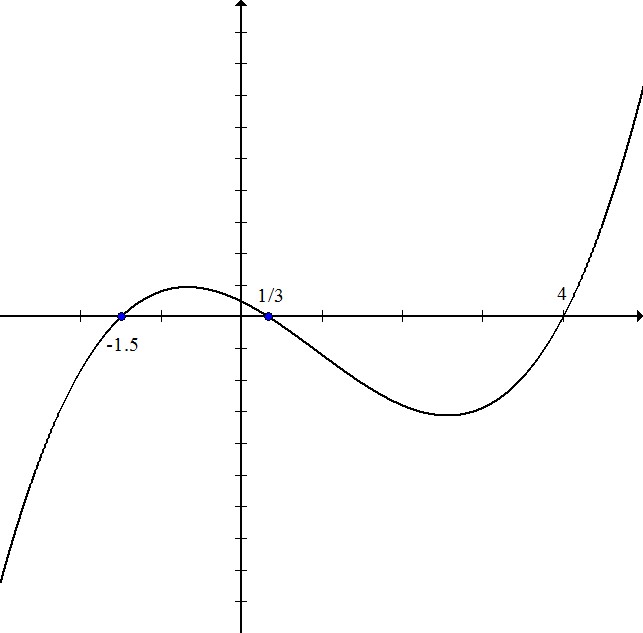
Write the equation for the polynomial in this graph:

The zeros for this polynomial are  .
.
This means that the factors are equal to zero when these values are plugged in for x.
 multiply both sides by 2
multiply both sides by 2
 so one factor is
so one factor is 
 multiply both sides by 3
multiply both sides by 3
 so one factor is
so one factor is 
 so one factor is
so one factor is 
Multiply these three factors:



The zeros for this polynomial are 
This means that the factors are equal to zero when these values are plugged in for x.





Multiply these three factors:
Compare your answer with the correct one above
Write the equation for the polynomial shown in this graph:

Write the equation for the polynomial shown in this graph:

The zeros of this polynomial are  . This means that the factors equal zero when these values are plugged in.
. This means that the factors equal zero when these values are plugged in.
One factor is 
One factor is 
The third factor is equivalent to  . Set equal to 0 and multiply by 2:
. Set equal to 0 and multiply by 2:


Multiply these three factors:


The graph is negative since it goes down then up then down, so we have to switch all of the signs:

The zeros of this polynomial are 
One factor is
One factor is
The third factor is equivalent to 
Multiply these three factors:
The graph is negative since it goes down then up then down, so we have to switch all of the signs:
Compare your answer with the correct one above
Write the equation for the polynomial in this graph:

Write the equation for the polynomial in this graph:

The zeros for this polynomial are  . That means that the factors are equal to zero when these values are plugged in.
. That means that the factors are equal to zero when these values are plugged in.
 or equivalently
or equivalently  multiply both sides by 4
multiply both sides by 4
 the first factor is
the first factor is 
 multiply both sides by 3
multiply both sides by 3
 the second factor is
the second factor is 
 the third factor is
the third factor is 
Multiply the three factors:



The zeros for this polynomial are 






Multiply the three factors:
Compare your answer with the correct one above
Write the equation for the polynomial in the graph:
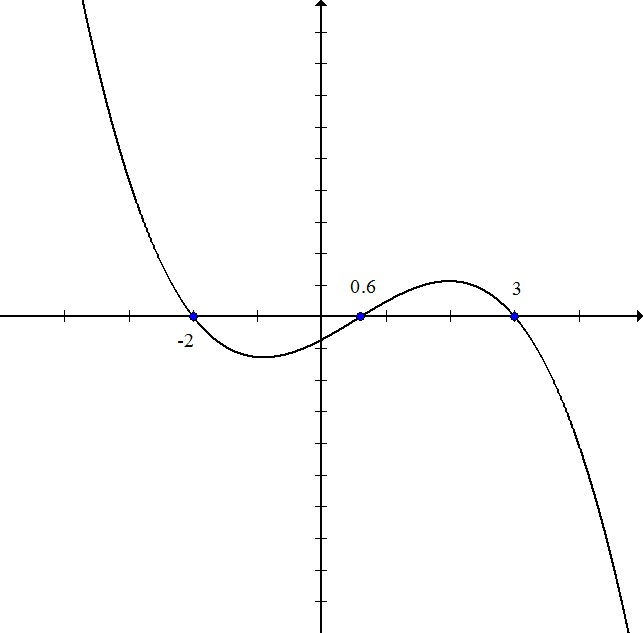
Write the equation for the polynomial in the graph:

The zeros of the polynomial are  . That means that the factors equal zero when these values are plugged in.
. That means that the factors equal zero when these values are plugged in.
The first factor is  or equivalently
or equivalently  multiply both sides by 5:
multiply both sides by 5:

The second and third factors are  and
and 
Multiply:



Because the graph goes down-up-down instead of the standard up-down-up, the graph is negative, so change all of the signs:

The zeros of the polynomial are 
The first factor is 

The second and third factors are 
Multiply:
Because the graph goes down-up-down instead of the standard up-down-up, the graph is negative, so change all of the signs:
Compare your answer with the correct one above