Limits - Pre-Calculus
Card 0 of 20
What are the discontinuities in the following function and what are their types?

What are the discontinuities in the following function and what are their types?
Since the factor  is in the numerator and the denominator, there is a removable discontinuity at
is in the numerator and the denominator, there is a removable discontinuity at  . The function is not defined at
. The function is not defined at  , but function would move towards the same point for the resultant function
, but function would move towards the same point for the resultant function  .
.
Since the factor cannot be factored out, there is an infinite discontinuity at
cannot be factored out, there is an infinite discontinuity at  . The denominator will get very small and the numerator will move toward a fixed value.
. The denominator will get very small and the numerator will move toward a fixed value.
There is no discontinuity at all at  . The function simply evaluates to zero at this point.
. The function simply evaluates to zero at this point.
Since the factor 



Since the factor

There is no discontinuity at all at 
Compare your answer with the correct one above
Find the domain where the following function is continuous:

Find the domain where the following function is continuous:
The function in the numerator factors to:

so if we cancel the x+3 in the numerator and denominator we have the same function but it is continuous. The  gives us a hole at x=-3 so our function is not continuous at x=-3.
gives us a hole at x=-3 so our function is not continuous at x=-3.
The function in the numerator factors to:
so if we cancel the x+3 in the numerator and denominator we have the same function but it is continuous. The 
Compare your answer with the correct one above
Determine if the function  is continuous at
is continuous at  using limits.
using limits.
Determine if the function 

In order to determine if a function is continuous at a point three things must happen.
-
Taking the limit from the lefthand side of the function towards a specific point exists.
-
Taking the limit from the righthand side of the function towards a specific point exists.
-
The limits from 1) and 2) are equal and equal the value of the original function at the specific point in question.
In our case,
-

-

-

Because all of these conditions are met, the function is continuous at 0.
In order to determine if a function is continuous at a point three things must happen.
-
Taking the limit from the lefthand side of the function towards a specific point exists.
-
Taking the limit from the righthand side of the function towards a specific point exists.
-
The limits from 1) and 2) are equal and equal the value of the original function at the specific point in question.
In our case,
Because all of these conditions are met, the function is continuous at 0.
Compare your answer with the correct one above
Determine if  is continuous on all points of its domain.
is continuous on all points of its domain.
Determine if 
First, find that at any point where  ,
,  .
.
Then find that
 and
and  .
.
As these are all equal, it can be determined that the function is continuous on all points of its domain.
First, find that at any point where 

Then find that


As these are all equal, it can be determined that the function is continuous on all points of its domain.
Compare your answer with the correct one above
Let  . Determine if the function is continuous using limits.
. Determine if the function is continuous using limits.
Let 
As  approaches
approaches  , the function
, the function  approaches
approaches  , which is undefined. However, if we factor
, which is undefined. However, if we factor  , we get:
, we get:


The  factors in the numerator and denominator cancel out, leaving
factors in the numerator and denominator cancel out, leaving  .
.
Therefore, our function is continuous at all values of  from
from  .
.
As 




The 

Therefore, our function is continuous at all values of 

Compare your answer with the correct one above
Let  .
.
Find  .
.
Let 
Find 

This is a graph of  . We know that
. We know that  is undefined; therefore, there is no value for
is undefined; therefore, there is no value for  . But as we take a look at the graph, we can see that as
. But as we take a look at the graph, we can see that as  approaches 0 from the left,
approaches 0 from the left,  approaches negative infinity.
approaches negative infinity.
This can be illustrated by thinking of small negative numbers.


NOTE: Pay attention to one-sided limit specifications, as it is easy to pick the wrong answer choice if you're not careful.
 is actually infinity, not negative infinity.
is actually infinity, not negative infinity.

This is a graph of 




This can be illustrated by thinking of small negative numbers.
NOTE: Pay attention to one-sided limit specifications, as it is easy to pick the wrong answer choice if you're not careful.

Compare your answer with the correct one above
The speed of a car traveling on the highway is given by the following function of time:

What can you say about the car's speed after a long time (that is, as  approaches infinity)?
approaches infinity)?
The speed of a car traveling on the highway is given by the following function of time:
What can you say about the car's speed after a long time (that is, as 
The function given is a polynomial with a term  , such that
, such that  is greater than 1.
is greater than 1.
Whenever this is the case, we can say that the whole function diverges (approaches infinity) in the limit as  approaches infinity.
approaches infinity.
This tells us that the given function is not a very realistic description of a car's speed for large  !
!
The function given is a polynomial with a term 

Whenever this is the case, we can say that the whole function diverges (approaches infinity) in the limit as 
This tells us that the given function is not a very realistic description of a car's speed for large 
Compare your answer with the correct one above
Evaluate the limit below:

Evaluate the limit below:
 will approach
will approach  when
when  approaches
approaches  , so
, so 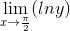 will be of type
will be of type  as shown below:
as shown below:

So, we can apply the L’ Hospital's Rule:


since:

hence:





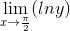

So, we can apply the L’ Hospital's Rule:
since:
hence:
Compare your answer with the correct one above
Calculate  .
.
Calculate 
This can be rewritten as follows:


![= \lim_{x\rightarrow \infty }\left [\left ( x^{2}-1 \right ) \cdot \sin \frac{1}{ x^{2}-1} \right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99922/gif.latex)

We can substitute  , noting that as
, noting that as  ,
,  :
:
 , which is the correct choice.
, which is the correct choice.
This can be rewritten as follows:
We can substitute 



Compare your answer with the correct one above
Evaluate the following limit.

Evaluate the following limit.
The function has a removable discontinuity at  . Once a factor of
. Once a factor of  is "divided out" the resultant function is
is "divided out" the resultant function is  , which evaluates to
, which evaluates to  as
as  approaches 0.
approaches 0.
The function has a removable discontinuity at 




Compare your answer with the correct one above
Find the limit as x approaches infinity

Find the limit as x approaches infinity
As x approaches infinity we only need to look at the highest order of polynomial in both the numerator and denominator. Then we compare the highest order polynomial in both the numerator and denominator. If the denominator is higher order our limit goes to zero, if the numerator is higher our order our limit goes to positive or negative infinity (depending on the sign of the highest order x term). If our numerator and denominator have the same order the limit goes to a/b where a is the coefficient for the highest order x in the numerator and b is the coefficient for the highest order x in the denominator.
Our numerator has higher order and the coefficient for the x to the fourth term is negative so our limit goes to negative infinity.
As x approaches infinity we only need to look at the highest order of polynomial in both the numerator and denominator. Then we compare the highest order polynomial in both the numerator and denominator. If the denominator is higher order our limit goes to zero, if the numerator is higher our order our limit goes to positive or negative infinity (depending on the sign of the highest order x term). If our numerator and denominator have the same order the limit goes to a/b where a is the coefficient for the highest order x in the numerator and b is the coefficient for the highest order x in the denominator.
Our numerator has higher order and the coefficient for the x to the fourth term is negative so our limit goes to negative infinity.
Compare your answer with the correct one above
Solve the limit as  approaches infinity.
approaches infinity.

Solve the limit as 
As x approaches infinity we only need to look at the highest order of polynomial in both the numerator and denominator. Then we compare the highest order polynomial in both the numerator and denominator. If the denominator is higher order our limit goes to zero, if the numerator is higher our order our limit goes to positive or negative infinity (depending on the sign of the highest order x term). If our numerator and denominator have the same order the limit goes to a/b where a is the coefficient for the highest order x in the numerator and b is the coefficient for the highest order x in the denominator.
For our equation the orders are the same in x for the numerator and denominator (both 4). So we divide the coefficients of the highest order x terms to get our limit and we get

As x approaches infinity we only need to look at the highest order of polynomial in both the numerator and denominator. Then we compare the highest order polynomial in both the numerator and denominator. If the denominator is higher order our limit goes to zero, if the numerator is higher our order our limit goes to positive or negative infinity (depending on the sign of the highest order x term). If our numerator and denominator have the same order the limit goes to a/b where a is the coefficient for the highest order x in the numerator and b is the coefficient for the highest order x in the denominator.
For our equation the orders are the same in x for the numerator and denominator (both 4). So we divide the coefficients of the highest order x terms to get our limit and we get
Compare your answer with the correct one above
Find the limit

Find the limit
When x=3/2 our denominator is zero so we can't just plug in 3/2 to get our limit. If we look at the numerator when x=3/2 we find that it is zero as well so our numerator can be factored. We see that our limit can be re-written as:

we then can cancel the 2x-3 from the numerator and denominator leaving us with:

and we can just plug in 3/2 into this limit to get

note: our function is not continuous at x=3/2 but the limit does exist.
When x=3/2 our denominator is zero so we can't just plug in 3/2 to get our limit. If we look at the numerator when x=3/2 we find that it is zero as well so our numerator can be factored. We see that our limit can be re-written as:
we then can cancel the 2x-3 from the numerator and denominator leaving us with:
and we can just plug in 3/2 into this limit to get
note: our function is not continuous at x=3/2 but the limit does exist.
Compare your answer with the correct one above
Solve the following limit:

Solve the following limit:
To solve this problem we need to expand the term in the numerator 
when we do that we get

the second degree x terms cancel and we get

now we can cancel our h's in the numerator and denominator to get

then we can just plug 0 in for h and we get our answer
To solve this problem we need to expand the term in the numerator
when we do that we get
the second degree x terms cancel and we get
now we can cancel our h's in the numerator and denominator to get
then we can just plug 0 in for h and we get our answer
Compare your answer with the correct one above
Finding limits of rational functions.
Let
 .
.
Find
 .
.
Finding limits of rational functions.
Let

Find

First factor the numerator to simplify the function.
 ,
,
so
 .
.
Now

 .
.
There is no denominator now, and hence no discontinuity. The limit can be found by simply plugging in  for
for  .
.
 .
.
First factor the numerator to simplify the function.

so

Now

There is no denominator now, and hence no discontinuity. The limit can be found by simply plugging in 


Compare your answer with the correct one above
The Michaelis-Menten equation is important in chemical kinetics. Suppose we are given the following equation relating K (reaction rate) and C (concentration):

Determine:

The Michaelis-Menten equation is important in chemical kinetics. Suppose we are given the following equation relating K (reaction rate) and C (concentration):
Determine:
There are a number of ways to solve this. Either we can solve by finding what K(C) evaluates to for larger values of C and see where they converge, i.e. :
K(10000) = 952.38
K(1000000) = 999.5
etc...
And we see that K(C) approaches 1000 for larger concentrations, C.
Or we can notice that the dominant term in the numerator is 1000C; dominant term in the denominator is C.
1000C / C = 1000, which will ultimately be our limit.
There are a number of ways to solve this. Either we can solve by finding what K(C) evaluates to for larger values of C and see where they converge, i.e. :
K(10000) = 952.38
K(1000000) = 999.5
etc...
And we see that K(C) approaches 1000 for larger concentrations, C.
Or we can notice that the dominant term in the numerator is 1000C; dominant term in the denominator is C.
1000C / C = 1000, which will ultimately be our limit.
Compare your answer with the correct one above
Let  .
.
Find 
 .
.
Let 
Find 

To find 
 here, you need only plug in
here, you need only plug in  for
for  :
:

To find 



Compare your answer with the correct one above
Evaluate
 .
.
Evaluate

Find a common denominator for both the upper and lower expressions and then simplify:

Find a common denominator for both the upper and lower expressions and then simplify:
Compare your answer with the correct one above
Find the limit of the function:

Find the limit of the function:
Substituting the value of  will yield
will yield  , which is not in indeterminate form. Therefore, L'Hopital's rule cannot be used.
, which is not in indeterminate form. Therefore, L'Hopital's rule cannot be used.
The question asks for the limit as x approaches to five from the right side in the graph. As the graph approaches closer and closer to  , the y-value decreases to negative infinity and will never touch
, the y-value decreases to negative infinity and will never touch  .
.
The correct answer is: 
Substituting the value of 

The question asks for the limit as x approaches to five from the right side in the graph. As the graph approaches closer and closer to 

The correct answer is:
Compare your answer with the correct one above
Find the limit.

Find the limit.
In the unsimplified form, the limit does not exist; however, the numerator can be factored and simplified.



In the unsimplified form, the limit does not exist; however, the numerator can be factored and simplified.
Compare your answer with the correct one above