Linear Inequalities - Pre-Calculus
Card 0 of 13
Solve for 

Solve for
In order to solve this equation, we must first isolate the absolute value. In this case, we do it by dividing both sides by  which leaves us with:
which leaves us with:


When we work with absolute value equations, we're actually solving two equations. So, our next step is to set up these two equations:
 and
and 
In both cases we solve for  by adding
by adding  to both sides, leaving us with
to both sides, leaving us with
 and
and 
This can be rewritten as 
In order to solve this equation, we must first isolate the absolute value. In this case, we do it by dividing both sides by 
When we work with absolute value equations, we're actually solving two equations. So, our next step is to set up these two equations:

In both cases we solve for 


This can be rewritten as
Compare your answer with the correct one above
Solve for 

Solve for
When we work with absolute value equations, we're actually solving two equations:
 and
and 
Adding  to both sides leaves us with:
to both sides leaves us with:
 and
and 
Dividing by  in order to solve for
in order to solve for  allows us to reach our solution:
allows us to reach our solution:
 and
and 
Which can be rewritten as:

When we work with absolute value equations, we're actually solving two equations:

Adding 

Dividing by 


Which can be rewritten as:
Compare your answer with the correct one above
Solve for 

Solve for
In order to solve for  we must first isolate the absolute value. In this case, we do it by dividing both sides by 2:
we must first isolate the absolute value. In this case, we do it by dividing both sides by 2:


As with every absolute value problem, we set up our two equations:
 and
and 
We isolate  by adding
by adding  to both sides:
to both sides:
 and
and 
Finally, we divide by  :
:
 and
and 
In order to solve for 
As with every absolute value problem, we set up our two equations:

We isolate 


Finally, we divide by 

Compare your answer with the correct one above
Solve for  .
.

Solve for 
Our first step in solving this equation is to isolate the absolute value. We do this by dividing both sides by 
 .
.
We then set up our two equations:

 and
and 
 .
.
Subtracting 4 from both sides leaves us with

 and
and 
 .
.
Lastly, we multiply both sides by 2, leaving us with  :
:
 and
and  .
.
Which can be rewritten as:

Our first step in solving this equation is to isolate the absolute value. We do this by dividing both sides by

We then set up our two equations:


Subtracting 4 from both sides leaves us with


Lastly, we multiply both sides by 2, leaving us with 


Which can be rewritten as:
Compare your answer with the correct one above
Solve for 

Solve for
We first need to isolate the absolute value, which we can do in two steps:
1. Add 2 to both sides:

2. Divide both sides by 4:


Our next step is to set up our two equations:
 and
and 
We can now solve the equations for  by subtracting both sides by 8:
by subtracting both sides by 8:
 and
and 
and then dividing them by 5:
 and
and 
Which can be rewritten as:

We first need to isolate the absolute value, which we can do in two steps:
1. Add 2 to both sides:
2. Divide both sides by 4:
Our next step is to set up our two equations:

We can now solve the equations for 

and then dividing them by 5:

Which can be rewritten as:
Compare your answer with the correct one above
Solve the following absolute value inequality:

Solve the following absolute value inequality:

First we need to get the expression with the absolute value sign by itself on one side of the inequality. We can do this by subtracting seven from both sides.

Next we need to set up two inequalities since the absolute value sign will make both a negative value and a positive value positive.

From here, subtract thirteen from both sides and then divide everything by four.



First we need to get the expression with the absolute value sign by itself on one side of the inequality. We can do this by subtracting seven from both sides.
Next we need to set up two inequalities since the absolute value sign will make both a negative value and a positive value positive.
From here, subtract thirteen from both sides and then divide everything by four.
Compare your answer with the correct one above
Solve the following absolute value inequality:

Solve the following absolute value inequality:

First we need to get the expression with the absolute value sign by itself on one side of the inequality. We can do this by dividing both sides by three.

We now have two equations:
 and
and 




So, our solution is 
First we need to get the expression with the absolute value sign by itself on one side of the inequality. We can do this by dividing both sides by three.
We now have two equations:



So, our solution is
Compare your answer with the correct one above
Solve the following inequality:

Solve the following inequality:

First we need to get the expression with the absolute value sign by itself on one side of the inequality. We can do this by subtracting two from both sides then dividing everything by three.


Since absolute value signs make both negative and positive values positive we need to set up a double inequality.

Now to solve for  subtract four from each side.
subtract four from each side.

First we need to get the expression with the absolute value sign by itself on one side of the inequality. We can do this by subtracting two from both sides then dividing everything by three.
Since absolute value signs make both negative and positive values positive we need to set up a double inequality.
Now to solve for 
Compare your answer with the correct one above
Solve for  :
:

Solve for 
If  , then either
, then either  or
or  based on the meaning of the absolute value function. We have to solve for both cases.
based on the meaning of the absolute value function. We have to solve for both cases.
a)  subtract 5 from both sides
subtract 5 from both sides
 divide by -2, which will flip the direction of the inequality
divide by -2, which will flip the direction of the inequality

Even if we didn't know the rule about flipping the inequality, this answer makes sense - for example,  , and
, and  .
.
b)  subtract 5 from both sides
subtract 5 from both sides
 divide by -2, once again flipping the direction of the inequality
divide by -2, once again flipping the direction of the inequality

If 


a) 

Even if we didn't know the rule about flipping the inequality, this answer makes sense - for example, 

b) 

Compare your answer with the correct one above
Solve the absolute value inequality.

Solve the absolute value inequality.
First, simplify so that the absolute value function is by itself on one side of the inequality.
 .
.
Note that the symbol flipps when you divide both sides by  .
.
Next, the two inequalities that result after removing the absolute value symbols are
 and
and  .
.
When you simplify the two inequalities, you get
 and
and  .
.
Thus, the solution is
 .
.
First, simplify so that the absolute value function is by itself on one side of the inequality.

Note that the symbol flipps when you divide both sides by 
Next, the two inequalities that result after removing the absolute value symbols are


When you simplify the two inequalities, you get


Thus, the solution is

Compare your answer with the correct one above
To solve absolute value inequalities, you have to write it two different ways. But first, divide out the 4 on both sides so that there is just the absolute value on the left side. Then, write it normally, as you see it:  and then flip the side and make the right side negative:
and then flip the side and make the right side negative:  . Then, solve each one. Your answers are
. Then, solve each one. Your answers are  and
and  .
.
To solve absolute value inequalities, you have to write it two different ways. But first, divide out the 4 on both sides so that there is just the absolute value on the left side. Then, write it normally, as you see it: 



Compare your answer with the correct one above
Solve the following:

Solve the following:
To solve absolute value inequalities create two functions.
Simply remember that when solving inequalities with absolute values, you keep one the same and then flip the sign and inequality on the other.
Thus,


Then, you must write it in interval notation.
Thus,

To solve absolute value inequalities create two functions.
Simply remember that when solving inequalities with absolute values, you keep one the same and then flip the sign and inequality on the other.
Thus,
Then, you must write it in interval notation.
Thus,
Compare your answer with the correct one above
Solve and graph:

Solve and graph:
- Write
 as two simple inequalities:
as two simple inequalities:
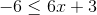

- Solve the inequalities:






- Write the final solution as a single compound inequality:

For interval notation:
![[-\frac{9}{6}, 3] = [-1 \frac{3}{6}, 3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/478528/gif.latex)
- Now graph:

- Write
as two simple inequalities:
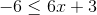
- Solve the inequalities:



- Write the final solution as a single compound inequality:
For interval notation:
- Now graph:

Compare your answer with the correct one above
