Graphing the Sine and Cosine Functions - Pre-Calculus

Card 0 of 20

Question

Which of the given functions has the greatest amplitude?

Answer

The amplitude of a function is the amount by which the graph of the function travels above and below its midline. When graphing a sine function, the value of the amplitude is equivalent to the value of the coefficient of the sine. Similarly, the coefficient associated with the x-value is related to the function's period. The largest coefficient associated with the sine in the provided functions is 2; therefore the correct answer is $2\sin(x)$ .

The amplitude is dictated by the coefficient of the trigonometric function. In this case, all of the other functions have a coefficient of one or one-half.

Compare your answer with the correct one above

Question

What is the amplitude of $y=3\sin\left(\frac{x}{5}\right)}$ ?

Answer

For any equation in the form $y=a\sin(bx)$ , the amplitude of the function is equal to $\left | a\right |$ .

In this case, and $b=\frac{1}{5}$ , so our amplitude is .

Compare your answer with the correct one above

Question

What is the amplitude of ?

Answer

The formula for the amplitude of a sine function is from the form:

.

In our function, .

Therefore, the amplitude for this function is .

Compare your answer with the correct one above

Question

Find the amplitude of the following trig function: $y=-2-3sin(2\theta-5)$

Answer

Rewrite $y=-2-3sin(2\theta-5)$ so that it is in the form of:

$y=-3sin(2\theta-5)-2$

The absolute value of is the value of the amplitude.

$\textup{Amplitude= }\left | A\right |= \left | -3\right |=3$

Compare your answer with the correct one above

Question

Find the amplitude of the function.

Answer

For the sine function

where $A\epsilon , \mathbb{R}$

the amplitude is given as $\left | A\right |$ .

As such the amplitude for the given function

is

$\left | 5\right |=5$ .

Compare your answer with the correct one above

Question

Given $F(t)=sin\left(\frac{x}{2}-4\right)$ , what is the period for the function?

Answer

The formula for the period of a sine/cosine function is $\frac{2\pi}{|B|}$ .

With the standard form being:

Since $B=\frac{1}{2}$ , the formula becomes $\frac{2\pi}{\frac{1}{2}}$ .

Simplified, the period is $4\pi$ .

Compare your answer with the correct one above

Question

What could be the function for the following graph?

Answer

What could be the function for the following graph?

Begin by realizing we are dealing with a periodic function, so sine and cosine are your best bet.

Next, note that the range of the function is $-2\leq y \leq 6$ and that the function goes through the point .

From this information, we can find the amplitude:

$A=\frac{6--2}{2}=\frac{8}{2}=4$

So our function must have a out in front.

Also, from the point , we can deduce that the function has a vertical translation of positive two.

The only remaining obstacle, is whether the function is sine or cosine. Recall that sine passes through , while cosine passes through . this means that our function must be a sine function, because in order to be a cosien graph, we would need a horizontal translation as well.

Thus, our answer is:

$y=4\sin(x)+2$

Compare your answer with the correct one above

Question

What is the period of this sine graph?

Answer

The graph has 3 waves between 0 and $2\pi$ , meaning that the length of each of the waves is $2\pi$ divided by 3, or $\frac{2}{3}\pi$ .

Compare your answer with the correct one above

Question

What is the period of this graph?

Answer

One wave of the graph goes exactly from 0 to $2\pi$ before repeating itself. This means that the period is $2\pi$ .

Compare your answer with the correct one above

Question

Please choose the best answer from the following choices.

Find the period of the following function.

Answer

The period is defined as the length of one wave of the function. In this case, one full wave is 180 degrees or $\pi$ radians. You can figure this out without looking at a graph by dividing $2\pi$ with the frequency, which in this case, is 2.

Compare your answer with the correct one above

Question

Please choose the best answer from the following choices.

Find the period of the following function in radians:

Answer

If you look at a graph, you can see that the period (length of one wave) is $2\pi$ . Without the graph, you can divide $2\pi$ with the frequency, which in this case, is 1.

Compare your answer with the correct one above

Question

Write the equation for a cosine graph with a minimum at $\left(\frac{ 3 \pi }{ 8 } , -5\right)$ and a maximum at $\left(\frac{ 11 \pi }{ 8 } , -1 \right)$ .

Answer

The equation for this graph will be in the form $y = A \cos (f (x - h)) + k$ where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.

To write this equation, it is helpful to sketch a graph:

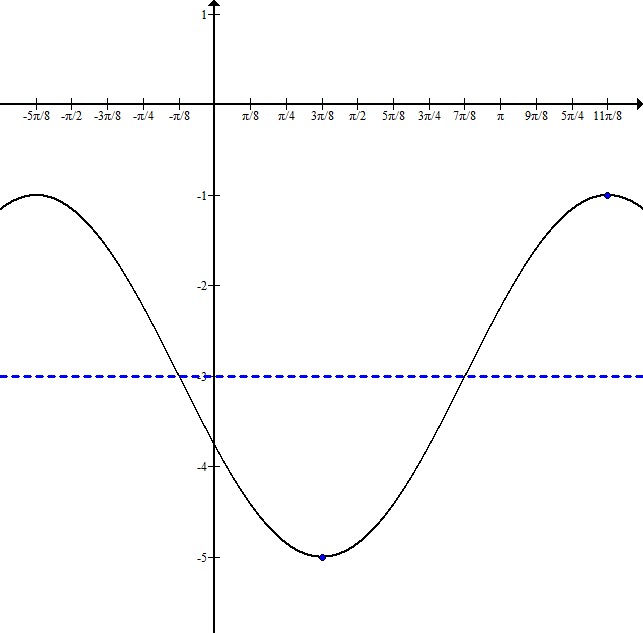
From sketching the maximum and the minimum, we can see that the graph is centered at and has an amplitude of 2.

The distance between the maximum and the minimum is half the wavelength. Here, it is $\frac{ 11 \pi }{ 8 } - \frac{ 3 \pi }{ 8 } = \frac{ 8 \pi }{ 8 } = \pi$ . That means that the full wavelength is $2 \pi$ , so the frequency is 1.

The minimum occurs in the middle of the graph, so to figure out where it starts, subtract $\pi$ from the minimum's x-coordinate:

$\frac{ 3 \pi }{ 8 } - \pi = \frac{ 3 \pi }{8 } - \frac{ 8 \pi }{ 8 } = \frac{ -5 \pi }{8 }$

This graph's equation is

$y = 2 \cos (x + \frac{ 5 \pi }{8 }) -3$ .

Compare your answer with the correct one above

Question

Give the period and frequency for the equation $y = 4 \sin (6x - \pi ) + 2$ .

Answer

Our equation is in the form $y = A \cdot \sin ( fx - h ) + k$

where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.

We can look at the equation and see that the frequency, , is .

The period is $\frac{ 2 \pi }{f }$ , so in this case $\frac{ 2 \pi }{6} = \frac{ \pi }{3}$ .

Compare your answer with the correct one above

Question

What is the period of the graph $y = -2 \cos (\frac { \pi }{8 } x + 1 )$ ?

Answer

The equation for this function is in the form $y = A \cos (fx - h) + k$

where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.

By looking at the equation, we can see that the frequency, , is $\frac{ \pi }{ 8 }$ .

The period is $\frac{ 2 \pi }{f }$ , so in this case $\frac{ 2 \pi }{ \frac{ \pi }{ 8 }} = 2 \pi \div \frac{ \pi }{ 8 } = \frac{ 2 \pi }{1} \cdot \frac{ 8}{\pi } = 16$ .

Compare your answer with the correct one above

Question

Find the phase shift of .

Answer

In the formula,

.

$\frac{C}{B}$ represents the phase shift.

Plugging in what we know gives us:

$\frac{C}{B}=\frac{-4}{2}$ .

Simplified, the phase is then .

Compare your answer with the correct one above

Question

Which equation would produce this graph?

Answer

This is the graph of sine, but shifted to the right $\frac{\pi}{2}$ units. To reflect this shift, $\frac{\pi}{2}$ should be subtracted from x.

Thus resulting in

$y=sin\left(x-\frac{\pi}{2}\right)$ .

Compare your answer with the correct one above

Question

Which equation would produce this sine graph?

Answer

The graph has an amplitude of 2 but has been shifted down 1:

In terms of the equation, this puts a 2 in front of sin, and -1 at the end.

This makes it easier to see that the graph starts \[is at 0\] where $x=\frac{\pi}{4}$ .

The phase shift is $\frac{\pi}{4}$ to the right, or $x-\frac{\pi}{4}$ .

Compare your answer with the correct one above

Question

Please choose the best answer from the following choices.

Describe the phase shift of the following function:

$y=sin(x+\pi )$

Answer

Since $\pi$ is being added inside the parentheses, there will be a horizontal shift. The goal is to maintain zero within the parentheses so you will shift left $\pi$ radians.

Compare your answer with the correct one above

Question

Write the equation for a sine graph with a maximum at $\left(\frac{ \pi }{8}, 3\right)$ and a minimum at $\left(\frac{ 9 \pi }{8 } , -1 \right)$ .

Answer

To write this equation, it is helpful to sketch a graph:

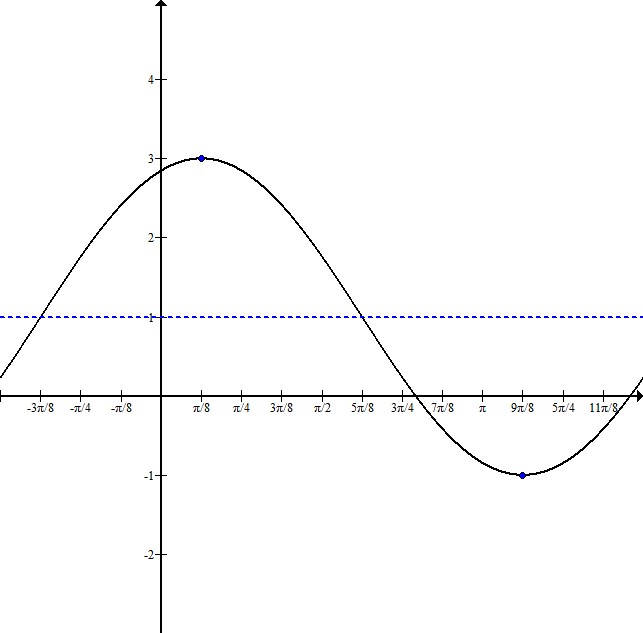
Indicating the maximum and minimum points, we can see that this graph has been shifted up 1, and it has an amplitude of 2.

The distance from the maximum to the minimum point is half the wavelength. In this case, the wavelength is $\frac{ 9 \pi }{ 8 } - \frac{ \pi }{8 } = \frac{ 8 \pi }{8 } = \pi$ . That means the full wavelength is $2 \pi$ , and the frequency is 1.

This sketch shows that the graph starts to the left of the y-axis. To figure out exactly where, subtract $\frac{ \pi }{2}$ from the maximum x-coordinate, $\frac{ \pi }{ 8 }$ :

$\frac{ \pi }{ 8 } - \frac{ \pi }{2} = \frac{ \pi }{8 } - \frac{ 4 \pi }{ 8 } = \frac{ - 3 \pi }{ 8 }$ .

Our equation will be in the form $y = A \cdot \sin ( f (x - h )) + k$ where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.

This graph has an equation of

$y = 2 \sin ( x + \frac{ 3 \pi }{ 8 } ) + 1$ .

Compare your answer with the correct one above

Question

Write the equation for a cosine graph with a maximum at $\left( \frac{ \pi }{3} , 3 \right)$ and a minimum at $\left(\frac{ 4 \pi }{3} , -3 \right)$ .

Answer

In order to write this equation, it is helpful to sketch a graph:

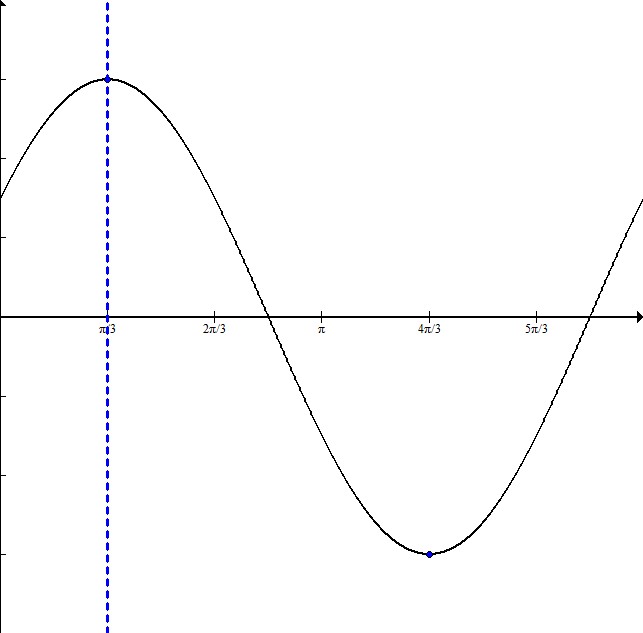
The dotted line is at $x = \frac{ \pi }{3}$ , where the maximum occurs and therefore where the graph starts. This means that the graph is shifted to the right $\frac{ \pi }{3}$ .

The distance from the maximum to the minimum is half the entire wavelength. Here it is $\frac{ 4 \pi }{3} - \frac{ \pi }{3} = \frac{ 3 \pi }{3} = \pi$ .

Since half the wavelength is $\pi$ , that means the full wavelength is $2 \pi$ so the frequency is just 1.

The amplitude is 3 because the graph goes symmetrically from -3 to 3.

The equation will be in the form $y = A \cdot \cos (f (x - h)) + k$ where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.

This equation is

$y = 3 \cos (x - \frac{ \pi } {3 })$ .

Compare your answer with the correct one above

Tap the card to reveal the answer