Graphing Functions - Pre-Calculus

The following matches the correct period with its corresponding trig function:

In other words, sin x, cos x, sec x, and csc x all repeat themselves every units. However, tan x and cot x repeat themselves more frequently, every units.

The graph has 3 waves between 0 and , meaning that the length of each of the waves is divided by 3, or .

In order to write this equation, it is helpful to sketch a graph:

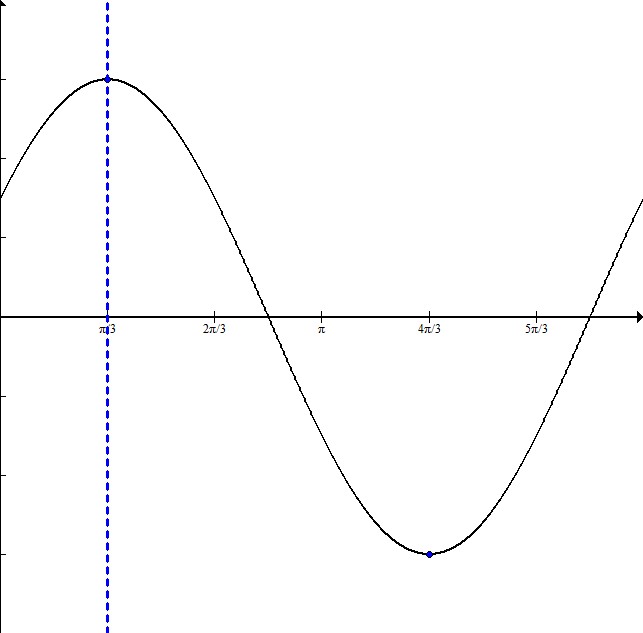
The dotted line is at , where the maximum occurs and therefore where the graph starts. This means that the graph is shifted to the right .

The distance from the maximum to the minimum is half the entire wavelength. Here it is .

Since half the wavelength is , that means the full wavelength is so the frequency is just 1.

The amplitude is 3 because the graph goes symmetrically from -3 to 3.

The equation will be in the form where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.

This equation is

.

In the formula,

.

represents the phase shift.

Plugging in what we know gives us:

.

Simplified, the phase is then .

The graph has an amplitude of 2 but has been shifted down 1:

In terms of the equation, this puts a 2 in front of sin, and -1 at the end.

This makes it easier to see that the graph starts \[is at 0\] where .

The phase shift is to the right, or .

The form of the equation will be

First, think about all possible values of A that could give you an amplitude of 3. Either A = -3 or A = 3 could each produce amplitude = 3. Be sure to look for answer choices that satisfy either of these.

Secondly, we know that the period is . Normally we know what B is and need to find the period, but this is the other way around. We can still use the same equation and solve:

. You can cross multiply to solve and get B = 4.

Finally, we need to find a value of C that satisfies

. Cross multiply to get:

.

Next, plug in B= 4 to solve for C:

Putting this all together, the equation could either be:

or

A common way to make sense of all of the transformations that can happen to a trigonometric function is the following. For the equations y = A sin(Bx + C) + D,

• amplitude is |A|
• period is 2/|B|
• phase shift is - C/B
• vertical shift is D

In our equation, A=-7, B=6, C=, and D=-4. Next, apply the above numbers to find amplitude, period, phase shift, and vertical shift.

To find amplitude, look at the coefficient in front of the sine function. A=-7, so our amplitude is equal to 7.

The period is 2/B, and in this case B=6. Therefore the period of this function is equal to 2/6 or /3.

To find the phase shift, take -C/B, or -/6. Another way to find this same value is to set the inside of the parenthesis equal to 0, then solve for x.
6x+=0
6x=-
x=-/6
Either way, our phase shift is equal to -/6.

The vertical shift is equal to D, which is -4.

y=-7\sin(6x+\pi)-4

A common way to make sense of all of the transformations that can happen to a trigonometric function is the following. For the equations y = A sin(Bx + C) + D,

• amplitude is |A|
• period is 2/|B|
• phase shift is - C/B
• vertical shift is D

In our equation, A=-1, B=1, C=-, and D=3. Next, apply the above numbers to find amplitude, period, phase shift, and vertical shift.

To find amplitude, look at the coefficient in front of the sine function. A=-1, so our amplitude is equal to 1.

The period is 2/B, and in this case B=1. Therefore the period of this function is equal to 2.

To find the phase shift, take -C/B, or . Another way to find this same value is to set the inside of the parenthesis equal to 0, then solve for x.
x-=0
x=
Either way, our phase shift is equal to .

The vertical shift is equal to D, which is 3.

A common way to make sense of all of the transformations that can happen to a trigonometric function is the following. For the equations y = A sin(Bx + C) + D,

• amplitude is |A|
• period is 2/|B|
• phase shift is - C/B
• vertical shift is D

In our equation, A=1, B=2, C=-3, and D=2. Next, apply the above numbers to find amplitude, period, phase shift, and vertical shift.

To find amplitude, look at the coefficient in front of the sine function. A=1, so our amplitude is equal to 1.

The period is 2/B, and in this case B=2. Therefore the period of this function is equal to .

To find the phase shift, take -C/B, or 3/2. Another way to find this same value is to set the inside of the parenthesis equal to 0, then solve for x.
2x-3=0
2x=3
x=3/2
Either way, our phase shift is equal to 3/2.

The vertical shift is equal to D, which is 2.

First, we need to compute , the slope. We can do this with the slope formula

, sometimes called "rise over run"

So we now have

Now in order to solve for we substitute one of our points into the equation we found. It doesn't matter which point we use, so we'll use .

We then have:

Which becomes .

Hence we take our found value for and plug it back into to get

.

Since our slope is , we can plug it into right away giving .

To solve for , we plug our given point in for and giving .

This will simplify to , or after subtracting the fraction.

Hence our answer is after plugging our values for and in.

Linear functions follow the form , where m is the slope and b is the y intercept. We can determine the equation of a linear function when we have the slope and a y intercept which is a starting point for drawing our line. If we need the equation of a line that passes through two points we use the point slope equation:

where the variables with numbers next to them correspond to places where you input the x and y from a single (same) coordinate pair.

Since we have two points, we can compute the slope of a line that passes between them. .

.

Now use the point slope formula:

distribute the right side

add 6 to both sides

which is the final answer.

Take a look at the coordinate pairs. Was it necessary to to use the point slope formula? The answer is no, since the coordinate pair (0,5) is already a y intercept. So all that was necessary was to compute the slope.

Bob starts out with 4 candies. Write the equation.

Every week, he earns 14 candies. Every week has a total of 7 days. Divide the amount of candies by the number of days to determine the number of candies Bob earn in a day.

Bob then earns 2 candies per day. Let represent the number of candies per day. Finish the incomplete equation.

To solve for the equation of this problem, we will need 2 points. Let the point be defined as , where is time in hours and represents the dollars Billy has earned.

Billy starts with three dollars in the first hour. Write the point.

At the end of eight hours, Billy has fifty dollars. Write the second point.

Write the slope-intercept formula.

Write slope formula.

Plug a point and the given slope to the slope-intercept formula to solve for the y-intercept.

Substitute this and the slope back into the slope-intercept equation.

Since Billy's earning is dependent on the time he works, rewrite the equation so that time is the independent variable, and amount earned is the dependent.

First find the reciprocal of the slope of the given function.

The perpendicular function is:

Now we must find the constant, , by using the given point that the perpendicular crosses.

solve for :

First find the reciprocal of the slope of the given function.

The perpendicular function is:

Now we must find the constant, , by using the given point that the perpendicular crosses.

solve for :

First find the reciprocal of the slope of the given function.

The perpendicular function is:

Now we must find the constant, , by using the given point that the perpendicular crosses.

solve for :

One way to determine algebraically if a function is an even function, or symmetric about the y-axis, is to substitute in for . When we do this, if the function is equivalent to the original, then the function is an even function. If not, it is not an even function.

For our function:

Thus the function is not symmetric about the y-axis.

One way to determine algebraically if a function is an even function, or symmetric about the y-axis, is to substitute in for . When we do this, if the function is equivalent to the original, then the function is an even function. If not, it is not an even function.

For our function:

Since this matches the original, our function is symmetric across the y-axis.