Exponential and Logarithmic Functions - Pre-Calculus

Card 0 of 20

Question

The amount of phosphorus present in a sample at a given time is given by the following equation:

$Q(t)=Q_0e^{-0.03t}$

Where is in days, is the amount of phosphorus after days, and is the initial amount of phosphorus at the beginning of the first day. What percent of the initial amount of phosphorus is left after days of decay?

Answer

The problem asks us for the percent that the amount of phosphorus after t days is of the original amount of phosphorus. If we think of this percentage with respect to the variables present in the equation, we can see that the following fraction expresses the amount of phosphorus after t days as a percentage of the initial amount of phosphorus:

$\frac{Q(t)}{Q_0}$

So if this is the fraction we want to solve for, we should divide both sides of the equation by to obtain this fraction on the left side of the equation:

$Q(t)=Q_0e^{-0.03t}$

$\frac{Q(t)}{Q_0}=\frac{Q_0e^{-0.03t}}{Q_0}$

$\frac{Q(t)}{Q_0}=e^{-0.03t}$

We now have the fraction we want to solve for in terms of just one variable, , for which we plug in 25 days to find the percentage of phosphorus left of the initial amount after 25 days:

$\frac{Q(25)}{Q_0}=e^{-0.03(25)}=0.47$

So after 25 days of decay, the amount of phosphorus is 47% of the initial amount.

Compare your answer with the correct one above

Question

The exponential decay of an element is given by the following function:

$Q(t)=Q_0e^{-0.04223t}$

Where is the amount of the element left after days, and is the initial amount of the element. If there are kg of the element left after days, what was the initial amount of the element?

Answer

The problem asks us for the initial amount of the element, so first let's solve our equation for :

$Q(t)=Q_0e^{-0.04223t}$

$Q_0=Q(t)e^{0.04223t}$

The problem tells us that 25 days has passed, which gives us , and it also tells us the amount left after 25 days, which gives us . Now that we have our equation for , we can plug in the given values to find the initial amount of the element:

$Q_0=Q(25)e^{0.04223(25)}=(37)e^{0.04223(25)}=106.3$ kg

Compare your answer with the correct one above

Question

The exponential decay of an element is given by the function:

$Q(t) = Q_oe^{-0.42t}$

In this function, is the amount of the element left after days, and is the initial amount of the element. If of the element is left after seven days, how much of the element was there to begin with, rounded to the nearest kilogram?

Answer

To find the initial amount, you must rearrange the equation to solve for :

$Q(t) = Q_oe^{-0.42t}$

Divide both sides by $e^{-0.42t}$ :

$Q_o = \frac{Q(t)}{e^{-0.42t}}$

Substituting in the values from the problem gives

$Q_o = \frac{25}{e^{-0.42(7)}} \approx 473:kg$

Compare your answer with the correct one above

Question

The exponential decay of an element is given by the function

$Q(t) = Q_o e^{-0.9t}$

In this function, is the amount left after days, and is the initial amount of the element. What percent of the element is left after ten days, rounded to the nearest whole percent?

Answer

To find the final percentage of the element left, we must rearrange the equation to solve for $e^{-0.9t}$ :

$\frac{Q(t)}{Q_o} = e^{-0.9t}$

Now, using the ten days as , we can solve for the percent of the element left after ten days:

$\frac{Q(10)}{Q_o} = e^{-0.9*10} \approx 0.0001 = 0.01% \approx 0%$

Compare your answer with the correct one above

Question

The exponential decay of an element is given by the function

$Q(t) = Q_o e^{-0.0327t}$

where is the amount of the element after days, and is the initial amount of the element. If of the element are left after four days, how much of the element was there initially, to the nearest tenth of a kilogram?

Answer

To solve for the initial amount, we must use rearrange the equation:

$Q_o = \frac{Q(t)}{e^{-0.0327t}}$

We now substitute the values given from the problem

$Q_o = \frac{Q(4)}{e^{-0.03274}} = \frac{3}{e^{-0.03274}} = 3.4:kg$

Compare your answer with the correct one above

Question

If you invest into a savings account which earns an interest rate per year, how much would it take for your deposit to double?

Answer

The equation of the value for this problem is

$\small R(1+i)^n=2R$ .

We can divide by R to get

$\small \small (1+i)^n=2,$ .

We want to solve for n in this case, which is the amount of years. If we use the natural log on both sides and properties of logarithms, we get

$\small \ln(1+i)^n=n\ln(1+i)=\ln2$ .

If we solve for n, we get

$\small n = \frac{\ln(2)}{\ln(1+i)}$

Compare your answer with the correct one above

Question

If you deposit into a savings account which earns a yearly interest rate, how much is in your account after two years?

Answer

Since we are investing for two years with a yearly rate of 5%, we will use the formula to calculate compound interest.

where

is the amount of money after time.

is the principal amount (initial amount).

is the interest rate.

is time.

Our amount after two years is:

$\small 100(1.05^2)=100(1.1025)=110.25$

Compare your answer with the correct one above

Question

If you deposit into a savings account which compounds interest every month, what is the expression for the amount of money in your account after years if you earn a nominal interest rate of compounded monthly?

Answer

Since is the nominal interest rate compounded monthly we write the interest term as $\frac{i}{12}$ as it is the effective monthly rate.

We compound for years which is months. Since our interest rate is compounded monthly our time needs to be in the same units thus, months will be the units of time.

Plugging this into the equation for compound interest gives us the expression:

$A=P\left(1+\frac{i}{c}\right)^{ct}$

$A=R\left(1+\frac{i}{12}\right)^{12\cdot 2}$

$A=\small \small R \left(1+\frac{i}{12}\right)^{24}$

Compare your answer with the correct one above

Question

John opens a savings account and deposits into it. This savings account gains interest per year. After years, John withdraws all the money, and deposits it into another savings account with interest per year. years later, John withdraws the money.

How much money does John have after this year period? (Assume compound interest in both accounts)

Answer

Plugging our numbers into the formula for compound interest, we have:

.

So John has about after the first three years.

After placing his money into the other savings account, he has

after more years.

So John has accumulated about .

Compare your answer with the correct one above

Question

How many years does it take for to grow into when the is deposited into a savings account that gains annual compound interest?

Answer

The correct answer is about years.

To find the number of years required, we solve the compound interest formula for .

The formula is as follows:

Substitute known values.

Divide by .

Take the natural log of both sides.

$\ln5 = \ln ((1.05)^t)$

Use the log power rule.

$\ln5 = t\ln1.03$

Divide by $\ln1.03$ .

$\frac{\ln5}{\ln1.03} = t$

use a calculator to simplify.

Compare your answer with the correct one above

Question

Suppose you took out a loan years ago that gains interest. Suppose that you haven't made any payments on it yet, and right now you owe on the loan. How much was the loan worth when you took it out?

Answer

The formula for the compund interest is as follows:

By substuting known values into the compound interest formula, we have:

$100000 = P(1.069)^{10}$ .

From here, substitute known values.

$\frac{100000}{1.069^{10}} = P$

Divide by $1.069^{10}$

Compare your answer with the correct one above

Question

There were 240mg of caffeine in the discontinued energy drink. The decay rate for caffeine in the human bloodstream is around 0.14. If Jackie drinks this energy drink around 8PM, how much caffeine will still be in her system at midnight?

Answer

Because this is a process taking place in the human body, we should use the exponential decay formula involving e:

$A=P*e^{rt}$

where A is the current amount, P is the initial amount, r is the rate of growth/decay, and t is time.

In this case, since the amount of caffeine is decreasing rather than increasing, use . Between 8PM and midnight, 4 hours pass, so use . The initial amount of caffeine is given as 240 mg, so use .

Now evaluate:

$\ A = 240\cdot e^{-0.14\cdot 4} \ \= 240\cdot e^{-0.56} \approx 240 \cdot 0.57 \ \= 137.1$

Compare your answer with the correct one above

Question

Stuff animals were a strange craze of the 90's. A Cat stuff animal with white paws sold for $6 in 1997. In 2015, the Cat will sell for $1015. What has been the approximate rate of growth for these stuff animal felines?

Answer

Use the formula for exponential growth where y is the current value, A is the initial value, r is the rate of growth, and t is time. Between 1997 and 2015, 18 years passed, so use . The stuffed animal was originally worth $6, so . It is now worth $1,015, so .

Our equation is now:

$1015 = 6*(1+r)^{18}$ divide by 6:

$169.1\overline{6}=(1+r)^{18}$ take both sides to the power of $\frac{1}{18}=0.0\overline{5}$ :

$1.329 \approx 1+r$ subtract 1

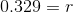
As a percent, r is about 33%.

Compare your answer with the correct one above

Question

Define a function as follows:

$f(x) = 4 ^{x+2} - 3$

Give the -intercept of the graph of .

Answer

The -coordinate ofthe -intercept of the graph of is 0, and its -coordinate is :

$f(x) = 4 ^{x+2} - 3$

$f(0) = 4 ^{0+2} - 3 = 4 ^{2} - 3 = 16 - 3 = 13$

The -intercept is the point .

Compare your answer with the correct one above

Question

What is the -intercept of $y = 4(2^{x})$ ?

Answer

The -intercept of a graph is the point on the graph where the -value is .

Thus, to find the -intercept, substitute and solve for .

Thus, we get:

$y = 4(2^{0}) = 4(1)=4$

Compare your answer with the correct one above

Question

Which of the following functions represents exponential decay?

Answer

Exponential decay describes a function that decreases by a factor every time increases by .

These can be recognizable by those functions with a base which is between and .

The general equation for exponential decay is,

where the base is represented by and .

Thus, we are looking for a fractional base.

The only function that has a fractional base is,

$y = \left(\frac{1}{3}\right)^{x}$ .

Compare your answer with the correct one above

Question

Does the function $y = 4^{x}$ have any -intercepts?

Answer

The -intercept of a function is where . Thus, we are looking for the -value which makes $0 = 4^{x}$ .

If we try to solve this equation for we get an error.

To bring the exponent down we will need to take the natural log of both sides.

Since the natural log of zero does not exist, there is no exponent which makes this equation true.

Thus, there is no -intercept for this function.

Compare your answer with the correct one above

Question

Choose the description below that matches the equation:

Answer

Exponential graphs can either decay or grow. This is based on the value of the base of the exponent. If the base is greater than , the graph will be growth. And, if the base is less than , then the graph will be decay. In this situation, our base is . Since this is greater than , we have a growth graph. Then, to determine the y-intercept we substitute . Thus, we get:

for the y-intercept.

Compare your answer with the correct one above

Question

Choose the description that matches the equation below:

$y = (\frac{1}{3})^{4x}$

Answer

Exponential graphs can either decay or grow. This is based on the value of the base of the exponent. If the base is greater than , the graph will be growth. And, if the base is less than , then the graph will be decay. In this situation, our base is $\frac{1}{3}$ . Since this is less than , we have a decay graph. Then, to determine the y-intercept we substitute . Thus, we get:

$y = (\frac{1}{3})^{(4\cdot 0)} = (\frac{1}{3})^0=1$ for the y-intercept.

Compare your answer with the correct one above

Question

Which of the following represents the graph of ?

Answer

Note that the negative sign in this function comes outside of the parentheses. This should show you that the bigger the number in parentheses, the lower the curve of the graph will go. Since this is an exponential function, the larger that the x value gets, then, the "more negative" this graph will go. The graph closest to zero on the left-hand side - where x is negative - and then shoots down and to the right rapidly when x gets larger is the correct graph.

Compare your answer with the correct one above

Tap the card to reveal the answer