Hyperbolas and Ellipses - Pre-Calculus
Card 0 of 20
Consider the following equation:

Classify the equation by its form when graphed.
Consider the following equation:
Classify the equation by its form when graphed.
Start with the equation

It would be helpful if we "complete the square" for both the x and y polynomials.


So by adding 9 and 900 we transform the equation into


And then by dividing 900, we see that the outcome is:

The standard equation for an ellipse is

With a center at 
Therefore this is the equation of an ellipse, with center 
Start with the equation
It would be helpful if we "complete the square" for both the x and y polynomials.
So by adding 9 and 900 we transform the equation into
And then by dividing 900, we see that the outcome is:
The standard equation for an ellipse is
With a center at
Therefore this is the equation of an ellipse, with center
Compare your answer with the correct one above
Express the following equation for an ellipse in standard form:

Express the following equation for an ellipse in standard form:
Remember that the equation for an ellipse in standard form looks like the following:

Where the point (h,k) gives the center of the ellipse, a is half the length of its axis in the x direction, and b is half the length of its axis in the y direction. We can see that this form has a 1 on the right side of the equation, so let's start by dividing both sides of our equation by 36 to get a 1 on the right side:



Now we can simplify the fractions on the right side of the equation, which gives us the equation for our ellipse in standard form:

This ellipse would have its center at (4,7), would be 6 units wide in the x direction, and 4 units wide in the y direction, because  so
so  , and
, and  so
so  .
.
Remember that the equation for an ellipse in standard form looks like the following:
Where the point (h,k) gives the center of the ellipse, a is half the length of its axis in the x direction, and b is half the length of its axis in the y direction. We can see that this form has a 1 on the right side of the equation, so let's start by dividing both sides of our equation by 36 to get a 1 on the right side:
Now we can simplify the fractions on the right side of the equation, which gives us the equation for our ellipse in standard form:
This ellipse would have its center at (4,7), would be 6 units wide in the x direction, and 4 units wide in the y direction, because 



Compare your answer with the correct one above
Find the endpoints of the major and minor axes of the ellipse described by the following equation:

Find the endpoints of the major and minor axes of the ellipse described by the following equation:
In order to find the endpoints of the major and minor axes of our ellipse, we must first remember what each part of the equation in standard form means:

The point given by (h,k) is the center of our ellipse, so we know the center of the ellipse in the problem is (8,-2), and we know that the end points of our major and minor axes will line up with the center either in the x or y direction, depending on the axis. The parts of the equation that will tell us the distance from the center to the endpoints of each axis are  and
and  . If we take the square root of each, a will give us the distance from the center to the endpoints in the positive and negative x direction, and b will give us the distance from the center to the endpoints in the positive and negative y direction:
. If we take the square root of each, a will give us the distance from the center to the endpoints in the positive and negative x direction, and b will give us the distance from the center to the endpoints in the positive and negative y direction:



Now it is important to consider the definition of major and minor axes. The major axis of an ellipse is the longer one, will the minor axis is the shorter one. We can see that b=5, which means the axis is longer in the y direction, so this is the major axis. To find the endpoints of the major axis, we'll go 5 units from the center in the positive and negative y direction, respectively, giving us:

Similarly, to find the endpoints of the minor axis, we'll go 2 units from the center in the positive and negative x direction, respectively, giving us:

In order to find the endpoints of the major and minor axes of our ellipse, we must first remember what each part of the equation in standard form means:
The point given by (h,k) is the center of our ellipse, so we know the center of the ellipse in the problem is (8,-2), and we know that the end points of our major and minor axes will line up with the center either in the x or y direction, depending on the axis. The parts of the equation that will tell us the distance from the center to the endpoints of each axis are 

Now it is important to consider the definition of major and minor axes. The major axis of an ellipse is the longer one, will the minor axis is the shorter one. We can see that b=5, which means the axis is longer in the y direction, so this is the major axis. To find the endpoints of the major axis, we'll go 5 units from the center in the positive and negative y direction, respectively, giving us:
Similarly, to find the endpoints of the minor axis, we'll go 2 units from the center in the positive and negative x direction, respectively, giving us:
Compare your answer with the correct one above
Express the following equation for a hyperbola in standard form:

Express the following equation for a hyperbola in standard form:
Remember that in order for the equation of a hyperbola to be in standard form, it must be written in one of the following two ways:


Where the point (h,k) gives the center of the hyperbola. In the first option, where the x term is in front of the y term, the hyperbola opens left and right. In the second option, where the y term is in front of the x term, the hyperbola opens up and down. In either case, the distance  tells how far above and below or to the left and right of the center the vertices of the hyperbola are. We can see that our equation is of the form given in the second option, as the y term appears first. All we must do to put it in standard form is obtain a 1 on the right side, so we'll divide both sides by 144:
tells how far above and below or to the left and right of the center the vertices of the hyperbola are. We can see that our equation is of the form given in the second option, as the y term appears first. All we must do to put it in standard form is obtain a 1 on the right side, so we'll divide both sides by 144:



Now we just simplify the fractions on the left side, and the equation of the hyperbola is in standard form:

Remember that in order for the equation of a hyperbola to be in standard form, it must be written in one of the following two ways:
Where the point (h,k) gives the center of the hyperbola. In the first option, where the x term is in front of the y term, the hyperbola opens left and right. In the second option, where the y term is in front of the x term, the hyperbola opens up and down. In either case, the distance 
Now we just simplify the fractions on the left side, and the equation of the hyperbola is in standard form:
Compare your answer with the correct one above
The equation of an ellipse,  , is
, is  . Which of the following is the correct center and foci of this ellipse?
. Which of the following is the correct center and foci of this ellipse?
The equation of an ellipse, 

Because our equation is already in the format
 ,
,
we do not have to manipulate the equation. The center of any ellipse in this form will always be  . So in this case, our center will be
. So in this case, our center will be  . To find the foci of the ellipse, we must use the equation
. To find the foci of the ellipse, we must use the equation  , where
, where  is the greater of the two denominators in our equation (
is the greater of the two denominators in our equation ( and
and  ),
),  is the lesser and
is the lesser and  is the distance from the center to the foci.
is the distance from the center to the foci.
We know that  and
and  .
.
By using  , we see that
, we see that  , so
, so  .
.
We now know that the two foci are going to be  units in either direction of the center along the greater axis.
units in either direction of the center along the greater axis.
Because the greater denominator is under our term containing  , our ellipse will have its greater axis going vertically, rather than horizontally. Therefore, our foci will be
, our ellipse will have its greater axis going vertically, rather than horizontally. Therefore, our foci will be  units above and below our center, at
units above and below our center, at  and
and  .
.
Because our equation is already in the format

we do not have to manipulate the equation. The center of any ellipse in this form will always be 







We know that 

By using 


We now know that the two foci are going to be 
Because the greater denominator is under our term containing 



Compare your answer with the correct one above
The equation of an ellipse,  , is
, is  . Which of the following is the correct eccentricity of this ellipse?
. Which of the following is the correct eccentricity of this ellipse?
The equation of an ellipse, 

The equation for the eccentricity of an ellipse is  , where
, where  is eccentricity,
is eccentricity,  is the distance from the foci to the center, and
is the distance from the foci to the center, and  is the square root of the larger of our two denominators.
is the square root of the larger of our two denominators.
Our denominators are  and
and  , so
, so  .
.
To find  , we must use the equation
, we must use the equation  , where
, where  is the square root of the smaller of our two denominators.
is the square root of the smaller of our two denominators.
This gives us 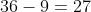 , so
, so  .
.
Therefore, we can see that
 .
.
The equation for the eccentricity of an ellipse is 



Our denominators are 


To find 


This gives us , so
.
Therefore, we can see that
.
Compare your answer with the correct one above
The equation of an ellipse,  , is
, is  . Which of the following are the correct end points of the MAJOR axis of this ellipse?
. Which of the following are the correct end points of the MAJOR axis of this ellipse?
The equation of an ellipse, 

First, we must determine if the major axis is a vertical axis or a horizontal axis. We look at our denominators,  and
and  , and see that the larger one is under the
, and see that the larger one is under the  -term. Therefore, we know that the greater axis will be a vertical one.
-term. Therefore, we know that the greater axis will be a vertical one.
To find out how far the end point are from the center, we simply take  . So we know the end points will be
. So we know the end points will be  units above and below our center. To find the center, we must remember that for
units above and below our center. To find the center, we must remember that for  ,
,
the center will be  .
.
So for our equation, the center will be  .
.  units above and below the center give us
units above and below the center give us  and
and  .
.
First, we must determine if the major axis is a vertical axis or a horizontal axis. We look at our denominators, 


To find out how far the end point are from the center, we simply take 


the center will be 
So for our equation, the center will be 



Compare your answer with the correct one above
Determine the equations for the asymptotes of the following hyperbola:

Determine the equations for the asymptotes of the following hyperbola:
Let us first remember what each part of the equation for a hyperbola in standard form means:


The point (h,k) gives the center of the hyperbola. In the first option, where the x term is in front of the y term, the hyperbola opens left and right. In the second option, where the y term is in front of the x term, the hyperbola opens up and down. In either case, the distance  tells how far above and below or to the left and right of the center the vertices of the hyperbola are. For each of these standard form expressions, respectively, the equations for the asymptotes are:
tells how far above and below or to the left and right of the center the vertices of the hyperbola are. For each of these standard form expressions, respectively, the equations for the asymptotes are:


So we can see that the equations are essentially the same, except that the slope  is used when the hyperbola opens left and right, and its reciprocal,
is used when the hyperbola opens left and right, and its reciprocal,  is used when the hyperbola opens up and down. We can see in the hyperbola for our problem that the x term appears first, so it opens left and right, which means we use the first option above for the equations of the asymptotes. Comparing the standard form equation with that given in the problem, we can determine h, k, a, and b:
is used when the hyperbola opens up and down. We can see in the hyperbola for our problem that the x term appears first, so it opens left and right, which means we use the first option above for the equations of the asymptotes. Comparing the standard form equation with that given in the problem, we can determine h, k, a, and b:




Now we now all of the values required for the asymptote formula, so we plug them in and get:

So our asymptotes are described by the following two equations:


Let us first remember what each part of the equation for a hyperbola in standard form means:
The point (h,k) gives the center of the hyperbola. In the first option, where the x term is in front of the y term, the hyperbola opens left and right. In the second option, where the y term is in front of the x term, the hyperbola opens up and down. In either case, the distance 
So we can see that the equations are essentially the same, except that the slope 

Now we now all of the values required for the asymptote formula, so we plug them in and get:
So our asymptotes are described by the following two equations:
Compare your answer with the correct one above
Find the center and the vertices of the following hyperbola:

Find the center and the vertices of the following hyperbola:
In order to find the center and the vertices of the hyperbola given in the problem, we must examine the standard form of a hyperbola:


The point (h,k) gives the center of the hyperbola. We can see that the equation in this problem resembles the second option for standard form above, so right away we can see the center is at:

In the first option, where the x term is in front of the y term, the hyperbola opens left and right. In the second option, where the y term is in front of the x term, the hyperbola opens up and down. In either case, the distance  tells how far above and below or to the left and right of the center the vertices of the hyperbola are. Our equation is in the first form, where the x term is first, so the hyperbola opens left and right, which means the vertices are a distance
tells how far above and below or to the left and right of the center the vertices of the hyperbola are. Our equation is in the first form, where the x term is first, so the hyperbola opens left and right, which means the vertices are a distance  to the left and right of the center. We can now calculate
to the left and right of the center. We can now calculate  by identifying it in our equation, and then go 3 units to the left and right of our center to find the following vertices:
by identifying it in our equation, and then go 3 units to the left and right of our center to find the following vertices:



In order to find the center and the vertices of the hyperbola given in the problem, we must examine the standard form of a hyperbola:
The point (h,k) gives the center of the hyperbola. We can see that the equation in this problem resembles the second option for standard form above, so right away we can see the center is at:
In the first option, where the x term is in front of the y term, the hyperbola opens left and right. In the second option, where the y term is in front of the x term, the hyperbola opens up and down. In either case, the distance 


Compare your answer with the correct one above
Which of the following is an equation for an ellipse written in standard form?
Which of the following is an equation for an ellipse written in standard form?
Remember that in order for the equation of an ellipse to be written in standard form, it must be written in one of the following two ways:


Where the point (h,k) gives the center of the ellipse, a is half the length of the axis for which it is the denominator, and b is half the length of the axis for which it is the denominator. Looking at our answer choices, we need one that involves addition, has different denominators under the x and y terms, and is equal to 1 on the right side of the equation. We can see that out of all the answer choices, the following is the only one that satisfies those requirements of standard form:

Remember that in order for the equation of an ellipse to be written in standard form, it must be written in one of the following two ways:
Where the point (h,k) gives the center of the ellipse, a is half the length of the axis for which it is the denominator, and b is half the length of the axis for which it is the denominator. Looking at our answer choices, we need one that involves addition, has different denominators under the x and y terms, and is equal to 1 on the right side of the equation. We can see that out of all the answer choices, the following is the only one that satisfies those requirements of standard form:
Compare your answer with the correct one above
Which of the following is an equation for a hyperbola written in standard form?
Which of the following is an equation for a hyperbola written in standard form?
In order for the equation of a hyperbola to be in standard form, it must be written in one of the following two ways:


Where the point (h,k) gives the center of the hyperbola, a is half the length of the axis for which it is the denominator, and b is half the length of the axis for which it is the denominator. The easiest requirements of standard form to identify are that the right side of the equation must be 1, there must be subtraction of the terms on the left side and not addition, and the denominators must be different for the x and y terms. Looking at our answer choices, we can see that the following equation is the only one which satisfies these requirements for the standard form of a hyperbola:

In order for the equation of a hyperbola to be in standard form, it must be written in one of the following two ways:
Where the point (h,k) gives the center of the hyperbola, a is half the length of the axis for which it is the denominator, and b is half the length of the axis for which it is the denominator. The easiest requirements of standard form to identify are that the right side of the equation must be 1, there must be subtraction of the terms on the left side and not addition, and the denominators must be different for the x and y terms. Looking at our answer choices, we can see that the following equation is the only one which satisfies these requirements for the standard form of a hyperbola:
Compare your answer with the correct one above
Find the equations for the asymptotes of the following hyperbola:

Find the equations for the asymptotes of the following hyperbola:
Remember that the standard form for the equation of a hyperbola is expressed in one of the following two ways:


Where a hyperbola of the first form would open left and right, and a hyperbola of the second form would open up and down. The formula for the asymptotes of either form are given below, respectively:


We can see that the equation given in the problem follows the second format of standard form, so we'll use the second equation above for finding the asymptotes of our hyperbola, which opens up and down. Looking at the equation for our hyperbola, we can see that h=-3, k= 5, a=4, and b=3. We have all the values we need, so we'll simply plug them into the formula for the asymptotes:


Remember that the standard form for the equation of a hyperbola is expressed in one of the following two ways:
Where a hyperbola of the first form would open left and right, and a hyperbola of the second form would open up and down. The formula for the asymptotes of either form are given below, respectively:
We can see that the equation given in the problem follows the second format of standard form, so we'll use the second equation above for finding the asymptotes of our hyperbola, which opens up and down. Looking at the equation for our hyperbola, we can see that h=-3, k= 5, a=4, and b=3. We have all the values we need, so we'll simply plug them into the formula for the asymptotes:
Compare your answer with the correct one above
What is the equation of an ellipse in standard form with the point  as its center, an
as its center, an  -axis length of
-axis length of  , and a
, and a  -axis length of
-axis length of  .
.
What is the equation of an ellipse in standard form with the point 




The equation of an ellipse in standard form is
 ,
,
where  is the center point,
is the center point,  is half the length of its axis in the
is half the length of its axis in the  direction, and
direction, and  is half the length of the axis in the
is half the length of the axis in the  direction.
direction.
In this instance, the center point 
 ,
,  , and
, and  . Therefore:
. Therefore:



The equation of an ellipse in standard form is

where 




In this instance, the center point 



Compare your answer with the correct one above
Find the center of the ellipse with the following equation:

Find the center of the ellipse with the following equation:
Recall that the standard form of the equation of an ellipse is
 , where
, where  is the center for the ellipse.
is the center for the ellipse.
For the equation given in the question,  and
and  .
.
The center of the ellipse is at 
Recall that the standard form of the equation of an ellipse is


For the equation given in the question, 

The center of the ellipse is at
Compare your answer with the correct one above
Find the center of the ellipse with the following equation:

Find the center of the ellipse with the following equation:
Recall that the standard form of the equation of an ellipse is
 , where
, where  is the center for the ellipse.
is the center for the ellipse.
For the equation given in the question,  and
and  .
.
The center of the ellipse is at  .
.
Recall that the standard form of the equation of an ellipse is


For the equation given in the question, 

The center of the ellipse is at 
Compare your answer with the correct one above
Find the center of the ellipse with the following equation:

Find the center of the ellipse with the following equation:
Recall that the standard form of the equation of an ellipse is
 , where
, where  is the center for the ellipse.
is the center for the ellipse.
For the equation given in the question,  and
and  .
.
The center of the ellipse is at  .
.
Recall that the standard form of the equation of an ellipse is


For the equation given in the question, 

The center of the ellipse is at 
Compare your answer with the correct one above
Find the center of the ellipse with the following equation:

Find the center of the ellipse with the following equation:
Start by putting the equation back into the standard equation of the ellipse:
 , where
, where  is the center for the ellipse.
is the center for the ellipse.
Group the  terms and
terms and  terms together.
terms together.


Factor out a  from the
from the  terms, and a
terms, and a  from the
from the  terms.
terms.

Now, complete the square. Remember to add the same amounts on both sides of the equation.


Now, divide both sides by  .
.

Finally, factor the equations to get the standard form of the equation for an ellipse.

Since  and
and  , the center for this ellipse is
, the center for this ellipse is  .
.
Start by putting the equation back into the standard equation of the ellipse:


Group the 

Factor out a 



Now, complete the square. Remember to add the same amounts on both sides of the equation.
Now, divide both sides by 
Finally, factor the equations to get the standard form of the equation for an ellipse.
Since 


Compare your answer with the correct one above
Find the center of the ellipse with the following equation:

Find the center of the ellipse with the following equation:
Start by putting the equation back into the standard equation of the ellipse:
 , where
, where  is the center for the ellipse.
is the center for the ellipse.
Group the  terms and
terms and  terms together.
terms together.


Factor out a  from the
from the  terms and a
terms and a  from the
from the  terms.
terms.

Now, complete the squares. Make sure you add the same amount on both sides!

Subtract  from both sides.
from both sides.

Now, divide both sides by  .
.

Finally, factor the terms to get the standard form of the equation of an ellipse.

Since  and
and  , the center of the ellipse is
, the center of the ellipse is  .
.
Start by putting the equation back into the standard equation of the ellipse:


Group the 

Factor out a 



Now, complete the squares. Make sure you add the same amount on both sides!
Subtract 
Now, divide both sides by 
Finally, factor the terms to get the standard form of the equation of an ellipse.
Since 


Compare your answer with the correct one above
Find the center of the ellipse with the following equation:

Find the center of the ellipse with the following equation:
Start by putting the equation back into the standard equation of the ellipse:
 , where
, where  is the center for the ellipse.
is the center for the ellipse.
Group the  terms and
terms and  terms together.
terms together.


Factor out a  from the
from the  terms and a
terms and a  from the
from the  terms.
terms.

Now, complete the squares. Remember to add the same amount on both sides!

Subtract  from both sides.
from both sides.

Divide both sides by  .
.

Finally, factor the terms to get the standard form of the equation of an ellipse.

Since  and
and  ,
,  is the center of this ellipse.
is the center of this ellipse.
Start by putting the equation back into the standard equation of the ellipse:


Group the 

Factor out a 



Now, complete the squares. Remember to add the same amount on both sides!
Subtract 
Divide both sides by 
Finally, factor the terms to get the standard form of the equation of an ellipse.
Since 


Compare your answer with the correct one above
Find the foci for the ellipse with the following equation:

Find the foci for the ellipse with the following equation:
Recall that the standard form of the equation of an ellipse is
 , where
, where  is the center for the ellipse.
is the center for the ellipse.
When  , the major axis will lie on the
, the major axis will lie on the  -axis and be horizontal. When
-axis and be horizontal. When  , the major axis will lie on the
, the major axis will lie on the  -axis and be vertical.
-axis and be vertical.
Recall also that the distance from the center to a focus,  , is given by the equation
, is given by the equation  when
when  , and the equation is
, and the equation is  when
when  .
.
When the major axis follows the  -axis, the points for the foci are
-axis, the points for the foci are  and
and  .
.
When the major axis follows the  -axis, the points for the foci are
-axis, the points for the foci are  and
and  .
.
For the given equation, the center is at  . Since
. Since  , the major-axis is vertical.
, the major-axis is vertical.
Plug in the values to solve for  .
.

The foci are then at the points  and
and  .
.
Recall that the standard form of the equation of an ellipse is


When 



Recall also that the distance from the center to a focus, 




When the major axis follows the 


When the major axis follows the 


For the given equation, the center is at 

Plug in the values to solve for 
The foci are then at the points 

Compare your answer with the correct one above