Identities and Properties - Pre-Algebra
Card 0 of 20
Which of the following statements demonstrates the identity property of addition?
Which of the following statements demonstrates the identity property of addition?
The identity property of addition states that there is a number 0, called the additive identity, that can be added to any number to yield that number as the sum. Of the four statements,

demonstrates this property.
The identity property of addition states that there is a number 0, called the additive identity, that can be added to any number to yield that number as the sum. Of the four statements,
demonstrates this property.
Compare your answer with the correct one above
Which statement demonatrates the additive identity property?
Which statement demonatrates the additive identity property?
By the additive identity property, zero added to a number yields that second number as the sum. This is shown by the statement
 .
.
By the additive identity property, zero added to a number yields that second number as the sum. This is shown by the statement

Compare your answer with the correct one above
Which of the following demonstrates the additive identity property?
Which of the following demonstrates the additive identity property?
Pre-algebra brings with it many different properties for memorization, and it is easy to forget one or mix two of them up. But maybe we can jog our memory by looking closely at the name of the property. The first word in the additive identity property is "additive". This tells us very quickly that the property involves addition. That means we can already eliminate any answer choices that don't involve adding, which in our case is the choice  .
.
With four choices left, we look at the next word in the name, "identity". The identity of something is what the thing is. In order for a spy to avoid being caught, he/she might change their idenity. They might take a different name, wear a wig, fake an accent, or dress differently. If the value of a number changes, its identity changes. In math, the only number I can add to any number without changing its value is 0. Therefore, we call 0 the additive identity because adding it preserves the identity of a number. This fact--namely that adding 0 to a number results in the same number--is what we call the Additive Identity Property.
If we look once more at our answer choices, the only one involving the addition of 0 to a number is the choice  . This is the correct answer.
. This is the correct answer.
Pre-algebra brings with it many different properties for memorization, and it is easy to forget one or mix two of them up. But maybe we can jog our memory by looking closely at the name of the property. The first word in the additive identity property is "additive". This tells us very quickly that the property involves addition. That means we can already eliminate any answer choices that don't involve adding, which in our case is the choice 
With four choices left, we look at the next word in the name, "identity". The identity of something is what the thing is. In order for a spy to avoid being caught, he/she might change their idenity. They might take a different name, wear a wig, fake an accent, or dress differently. If the value of a number changes, its identity changes. In math, the only number I can add to any number without changing its value is 0. Therefore, we call 0 the additive identity because adding it preserves the identity of a number. This fact--namely that adding 0 to a number results in the same number--is what we call the Additive Identity Property.
If we look once more at our answer choices, the only one involving the addition of 0 to a number is the choice 
Compare your answer with the correct one above
Which of the following best represents the additive identity property?
Which of the following best represents the additive identity property?
The additive identity property states that adding zero to any value will leave the value unchanged. The equations that will best describe this scenario is:


Zero is the additive identity.
The above two equations are the only possible correct answers.
The additive identity property states that adding zero to any value will leave the value unchanged. The equations that will best describe this scenario is:
Zero is the additive identity.
The above two equations are the only possible correct answers.
Compare your answer with the correct one above
Which of the following statements demonstrates the inverse property of addition?
Which of the following statements demonstrates the inverse property of addition?
The inverse property of addition states that for every real number, a number exists, called the additive inverse, such that the number and its inverse have sum 0. Of the statements given, only

demonstrates this property, so it is the correct choice.
The inverse property of addition states that for every real number, a number exists, called the additive inverse, such that the number and its inverse have sum 0. Of the statements given, only
demonstrates this property, so it is the correct choice.
Compare your answer with the correct one above
When is  neither positive nor negative?
neither positive nor negative?
When is 
The additive inverse of  is
is  . This means that when
. This means that when  is added to
is added to  the result is zero.
the result is zero.
 can be written as
can be written as  .
.
Since zero is the only number that is neither positive nor negative the answer is  .
.
The additive inverse of 





Since zero is the only number that is neither positive nor negative the answer is 
Compare your answer with the correct one above
What is the additive inverse of  ?
?
What is the additive inverse of 
The rule for Additive Inverse Property is  .
.
Using this rule if  ,
,

So the additive inverse is  .
.
The rule for Additive Inverse Property is 
Using this rule if 
So the additive inverse is 
Compare your answer with the correct one above
What is the additive inverse of 30?
What is the additive inverse of 30?
The question asks us what number added with 30 will equal zero. Write the mathematical equation that represents this scenario.

Subtract 30 from both sides.

The question asks us what number added with 30 will equal zero. Write the mathematical equation that represents this scenario.
Subtract 30 from both sides.
Compare your answer with the correct one above
Which of the following displays the additive inverse property?
Which of the following displays the additive inverse property?
The additive inverse property is when two numbers added together equal zero. So,

displays that property.
The additive inverse property is when two numbers added together equal zero. So,
displays that property.
Compare your answer with the correct one above
Which property is illustrated by the example?

Which property is illustrated by the example?
The associative property of addition states:

When considering only addition and subtraction, the order of operations does not matter.



The associative property of addition states:
When considering only addition and subtraction, the order of operations does not matter.
Compare your answer with the correct one above
Which of the following statements demonstrates the associative property of addition?
Which of the following statements demonstrates the associative property of addition?
The associative property of addition states that to add three numbers, any two can be added first, followed by adding the sum to the third. Of the statements given, only

demonstrates this property, so it is the correct choice.
The associative property of addition states that to add three numbers, any two can be added first, followed by adding the sum to the third. Of the statements given, only
demonstrates this property, so it is the correct choice.
Compare your answer with the correct one above
What property is being demonstrated?

What property is being demonstrated?
The Associative Property of Addition says that when we add more than two numbers the grouping of the addends does not change the sum.
The Associative Property of Addition says that when we add more than two numbers the grouping of the addends does not change the sum.
Compare your answer with the correct one above
Simplify.

Simplify.
Working left to right use the distributive property by multiplying the 4 to each term in parentheses.



Now, use the associative property to group like terms. Note that  cannot be combined because they are not like terms.
cannot be combined because they are not like terms.

Like terms can be combined with addition or subtraction.

Working left to right use the distributive property by multiplying the 4 to each term in parentheses.
Now, use the associative property to group like terms. Note that 
Like terms can be combined with addition or subtraction.
Compare your answer with the correct one above
What property can be applied to the following expression?

What property can be applied to the following expression?
The rule for Associative Property of Addition is 
Expression given in the question is: 
Hence the property is Associative of Addition.
The rule for Associative Property of Addition is
Expression given in the question is:
Hence the property is Associative of Addition.
Compare your answer with the correct one above
Use the "Associative of Addition" property to write the below expression in a different way.

Use the "Associative of Addition" property to write the below expression in a different way.
The rule for Associative Property of Addition is 
Using this rule, the expression  can be written as
can be written as 
The rule for Associative Property of Addition is
Using this rule, the expression 
Compare your answer with the correct one above
Which of the following displays the associative property of addition?
Which of the following displays the associative property of addition?
The associative property of addition states that you can group, or "associate," additive terms in any order and still get the same answer. Here  does just that: whether you add
does just that: whether you add 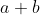 first and then add
first and then add  , or add
, or add  first and then
first and then  , as long as you add those three terms you'll get the same answer.
, as long as you add those three terms you'll get the same answer.
The associative property of addition states that you can group, or "associate," additive terms in any order and still get the same answer. Here 
first and then add
, or add
first and then
, as long as you add those three terms you'll get the same answer.
Compare your answer with the correct one above
If the below expression is written using the Associative Property of Multiplication, what are the values of  and
and  ?
?

If the below expression is written using the Associative Property of Multiplication, what are the values of 

The rule for Associative Property of Multiplication is 
Using this rule, we can determine that for the given expression  ,
,

The rule for Associative Property of Multiplication is
Using this rule, we can determine that for the given expression 
Compare your answer with the correct one above
Which set of equations illustrates the Associative property of Multiplication?
Which set of equations illustrates the Associative property of Multiplication?
 is the distributive property. Multiply each term in the parenthesis by the outside term.
is the distributive property. Multiply each term in the parenthesis by the outside term.
 is the Commutative property of Multiplication. The order of two like terms being multiplied does not change the product.
is the Commutative property of Multiplication. The order of two like terms being multiplied does not change the product.
 is the Multiplicative Identity property. Anything multiplied by 1 does not change.
is the Multiplicative Identity property. Anything multiplied by 1 does not change.
 is Associative property of Multiplication. The grouping of terms does not change their product as long as all terms remain in the equation. Try the green equation without the variables to see for yourself.
is Associative property of Multiplication. The grouping of terms does not change their product as long as all terms remain in the equation. Try the green equation without the variables to see for yourself.




Compare your answer with the correct one above
Which of the following best represents the associative property of multiplication?
Which of the following best represents the associative property of multiplication?
The property states that changing the order of multiplying any two numbers will not change the final answer.

Looking at the answer choices:
The answer  is the best choice.
is the best choice.
The property states that changing the order of multiplying any two numbers will not change the final answer.
Looking at the answer choices:
The answer 
Compare your answer with the correct one above
Which of the following displays the associative property of multiplication?
Which of the following displays the associative property of multiplication?
The associative property of multiplication states that you can multiply numbers together in any order, and the answer will not change. Therefore,

displays the associative property of multiplication since the two sides are equal no matter which set of parentheses you solve first.
The associative property of multiplication states that you can multiply numbers together in any order, and the answer will not change. Therefore,
displays the associative property of multiplication since the two sides are equal no matter which set of parentheses you solve first.
Compare your answer with the correct one above