Graphing Lines - Pre-Algebra
Card 0 of 20
A line graphed on the coordinate plane below. 
Give the equation of the line in slope intercept form.
A line graphed on the coordinate plane below.
Give the equation of the line in slope intercept form.
The slope of the line is 
and the y-intercept is 
.
The equation of the line is 
.
The slope of the line is
The equation of the line is
Compare your answer with the correct one above
The equation of a line is 
.
What are the slope and the y-intercept?
The equation of a line is
What are the slope and the y-intercept?
The equation of the line is written in slope-intercept form, 
, where 
is the slope and 
is the y-intercept. In this example, the y-intercept is a negative number.
The equation of the line is written in slope-intercept form,
Compare your answer with the correct one above
What is the slope of the line 
?
What is the slope of the line
In the standard form of a line 
the slope is represented by the variable 
.
In this case the line 
has a slope of 
.
The answer is 
.
In the standard form of a line
In this case the line
The answer is
Compare your answer with the correct one above
What is the slope of the line that contains the points
and 
What is the slope of the line that contains the points
To find the slope of a line with two points you must properly plug the points into the slope equation for two points which is
We must then properly assign the points to the equation as 
and 
.
In this case we will make 
our 
and 
our 
.
Plugging the points into the equation yields
Perform the math to arrive at
The answer is 
.
To find the slope of a line with two points you must properly plug the points into the slope equation for two points which is
We must then properly assign the points to the equation as
In this case we will make
Plugging the points into the equation yields
Perform the math to arrive at
The answer is
Compare your answer with the correct one above
What is the y-intercept of the line 
?
What is the y-intercept of the line
The y-intercept is the point at which the line intersects the y-axis.
It does this at 
.
We plug 
in for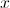 
in our equation, 
, to give us 
.
Anything multiplied by 
is 
, so 
.
Our coordinates for the y-intercept are 
.
The y-intercept is the point at which the line intersects the y-axis.
It does this at
We plug
Anything multiplied by
Our coordinates for the y-intercept are
Compare your answer with the correct one above
What is the slope of the line that contains the points 
and 
?
What is the slope of the line that contains the points
To find the slope of a line with two points we must properly plug the points into the slope equation: 
We must then assign the variables and .
In this case we will plug in 
for and 
for .
Plugging the points into the equation yields 
.
Perform the math to arrive at 
.
The answer is
.
To find the slope of a line with two points we must properly plug the points into the slope equation:
We must then assign the variables
In this case we will plug in
Plugging the points into the equation yields
Perform the math to arrive at
The answer is
Compare your answer with the correct one above
What is the slope of the line with the equation 
?
What is the slope of the line with the equation
In the standard form equation of a line, 
, the slope is represented by the variable 
.
In this case the line 
has a slope of 
.
Therefore the answer is 
.
In the standard form equation of a line,
In this case the line
Therefore the answer is
Compare your answer with the correct one above
What is the slope of the line 
?
What is the slope of the line
In the slope-intercept form of a line, , the slope is represented by the variable .
In this case the line
has a slope of 
.
The answer is 
.
In the slope-intercept form of a line,
In this case the line
has a slope of
The answer is
Compare your answer with the correct one above
What is the y-intercept of the line 
?
What is the y-intercept of the line
In the slope-intercept form of a line,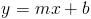 
, the y-intercept is when the line intersects the y-axis.
It does this at .
So we plug in for 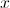in our equation
to give us
Anything multiplied by is so
Our coordinates for the y-intercept are 
.
In the slope-intercept form of a line,
It does this at
So we plug
to give us
Anything multiplied by
Our coordinates for the y-intercept are
Compare your answer with the correct one above
What is the slope of a line that is parallel to 
?
What is the slope of a line that is parallel to
Parallel lines have the same slope.
If an equation is in slope-intercept form, 
, we take the 
from our equation and set it equal to the slope of our parallel line.
In this case 
.
The slope of our parallel line is 
.
Parallel lines have the same slope.
If an equation is in slope-intercept form,
In this case
The slope of our parallel line is
Compare your answer with the correct one above
What is the slope of a line that is perpendicular to 
?
What is the slope of a line that is perpendicular to
The slope of a perpendicular lines has the negative reciprocal of the slope of the original line.
If an equation is in slope-intercept form, , we use the from our equation as our original slope.
In this case 
First flip the sign 
To find the reciprocal you take the integer and make it a fraction by placing a 
over it. If it is already a fraction just flip the numerator and denominator.
Do this to make the slope
The slope of the perpendicular line is
.
The slope of a perpendicular lines has the negative reciprocal of the slope of the original line.
If an equation is in slope-intercept form,
In this case
First flip the sign
To find the reciprocal you take the integer and make it a fraction by placing a
Do this to make the slope
The slope of the perpendicular line is
Compare your answer with the correct one above
What is the slope of the line that contains the points, 
and 
?
What is the slope of the line that contains the points,
To find the slope of a line with two points you must properly plug the points into the slope equation for two points which looks like
We must then properly assign the points to the equation as and .
In this case we will make 
our , and 
our .
Plugging the points into the equation yields
Perform the math to arrive at
The answer is 
.
To find the slope of a line with two points you must properly plug the points into the slope equation for two points which looks like
We must then properly assign the points to the equation as
In this case we will make
Plugging the points into the equation yields
Perform the math to arrive at
The answer is
Compare your answer with the correct one above
What is the slope of the line that contains the points, 
and 
?
What is the slope of the line that contains the points,
To find the slope of a line with two points you must properly plug the points into the slope equation for two points which looks like
We must then properly assign the points to the equation as and .
In this case we will make 
our and 
our .
Plugging the points into the equation yields
Perform the math to arrive at
The answer is 
.
To find the slope of a line with two points you must properly plug the points into the slope equation for two points which looks like
We must then properly assign the points to the equation as
In this case we will make
Plugging the points into the equation yields
Perform the math to arrive at
The answer is
Compare your answer with the correct one above
Which of the follow lines is parallel to:
Which of the follow lines is parallel to:
It is known that parallel lines have the same slope and therefore a line that is parallel to:
MUST have the same slope of 
.
It is known that parallel lines have the same slope and therefore a line that is parallel to:
MUST have the same slope of
Compare your answer with the correct one above
Write an equation in point-slope form for a line parallel to the line 
that goes through the point: 
.
Write an equation in point-slope form for a line parallel to the line
that goes through the point:
You know that point-slope form is: 
and therefore you must look at the slope of your equation given which is 
.
From there you just plug in what is given:
for 
,
for 
,
and 
for 
You know that point-slope form is:
and therefore you must look at the slope of your equation given which is
From there you just plug in what is given:
and
Compare your answer with the correct one above
What is the slope-intercept form of a line?
What is the slope-intercept form of a line?
The slope-intercept form of a line is 
.
The slope-intercept form of a line is
Compare your answer with the correct one above
What is the slope of the following line:
What is the slope of the following line:
To be able to identify the slope of a line, we need to get it in the form of
.
To do this we need to change the coefficient of y to be 
instead of 
. To do this, divide both sides of the equation by 
.
Now we can tell what the value of m, or the slope, is: 
To be able to identify the slope of a line, we need to get it in the form of
To do this we need to change the coefficient of y to be
Now we can tell what the value of m, or the slope, is:
Compare your answer with the correct one above
and 
are two points on a line. What is the slope of this line?
The slope of the line is determined by 
. In other words, we can use the formula 
.
Let's choose the coordinate 
to be (
, 
) and 
to be (
, 
).
We can now use the formula above:
The slope of the line is determined by
Let's choose the coordinate
We can now use the formula above:
Compare your answer with the correct one above
What is the slope of a line containing the points 
and 
?
What is the slope of a line containing the points
The formula to calculate slope between two points in a line is 
, for points 
and 
.
If we pick 
as our 
and 
as our 
, then:
This simplifies to 
, which can be reduced to 
The formula to calculate slope between two points in a line is
If we pick
This simplifies to
Compare your answer with the correct one above
What is the slope and y-intercept of the equation
What is the slope and y-intercept of the equation
The slope intercept formula is:
The slope intercept formula is:
Compare your answer with the correct one above