Separation of Variables - Partial Differential Equations
Card 0 of 1
Question
Solve for the general solution using separation of variables.
Given the following information:
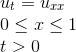


Solve for the general solution using separation of variables.
Given the following information:
Answer
Since the question states to use separation of variables the solution looks as follows.

Let

therefore the partial differential equation becomes

 is some constant therefore making the ordinary differential equation,
is some constant therefore making the ordinary differential equation,

In this particular case the constant must be negative.

Solving for  and
and  results in the following.
results in the following.
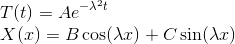
From here solve for the general transient solution
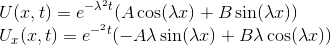
Lastly apply the boundary conditions to solve for the constants and in turn solve the general solution.

Since the question states to use separation of variables the solution looks as follows.
Let
therefore the partial differential equation becomes

In this particular case the constant must be negative.
Solving for 

From here solve for the general transient solution
Lastly apply the boundary conditions to solve for the constants and in turn solve the general solution.
Compare your answer with the correct one above
Tap the card to reveal the answer