Triangles - ISEE Upper Level Mathematics Achievement
Card 0 of 20
Which of the following is true about a triangle with two angles that measure  and
and  ?
?
Which of the following is true about a triangle with two angles that measure 

The sum of the two given angles is 90 degrees, which means that the third angle should be a right angle (90 degrees). We also know that two of the angles are equal. Therefore, the triangle is right and isosceles.
The sum of the two given angles is 90 degrees, which means that the third angle should be a right angle (90 degrees). We also know that two of the angles are equal. Therefore, the triangle is right and isosceles.
Compare your answer with the correct one above
What is the value of x in a right triangle if the two acute angles are equal to 5x and 25x?
What is the value of x in a right triangle if the two acute angles are equal to 5x and 25x?
In a right triangle, there is one right angle of 90 degrees, while the two acute angles add up to 90 degrees.
Given that the two acute angles are equal to 5x and 25x, the value of x can be calculated with the equation below:



In a right triangle, there is one right angle of 90 degrees, while the two acute angles add up to 90 degrees.
Given that the two acute angles are equal to 5x and 25x, the value of x can be calculated with the equation below:
Compare your answer with the correct one above
One of the base angles of an isosceles triangle is  . Give the measure of the vertex angle.
. Give the measure of the vertex angle.
One of the base angles of an isosceles triangle is 
The base angles of an isosceles triangle are always equal. Therefore both base angles are  .
.
Let  the measure of the third angle. Since the sum of the angles of a triangle is
the measure of the third angle. Since the sum of the angles of a triangle is 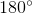 , we can solve accordingly:
, we can solve accordingly:

The base angles of an isosceles triangle are always equal. Therefore both base angles are 
Let 
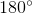
Compare your answer with the correct one above
Which of the following is true about a triangle with two angles that measure  and
and  ?
?
Which of the following is true about a triangle with two angles that measure 

A triangle must have at least two acute angles; however, a triangle with angles that measure  and
and  could have at most one acute angle, an impossible situation. Therefore, this triangle is nonexistent.
could have at most one acute angle, an impossible situation. Therefore, this triangle is nonexistent.
A triangle must have at least two acute angles; however, a triangle with angles that measure 

Compare your answer with the correct one above
Which of the following is true about a triangle with two angles that measure  each?
each?
Which of the following is true about a triangle with two angles that measure 
A triangle must have at least two acute angles; however, a triangle with angles that measure  would have two obtuse angles and at most one acute angle. This is not possible, so this triangle cannot exist.
would have two obtuse angles and at most one acute angle. This is not possible, so this triangle cannot exist.
A triangle must have at least two acute angles; however, a triangle with angles that measure 
Compare your answer with the correct one above
One angle of an isosceles triangle has measure  . What are the measures of the other two angles?
. What are the measures of the other two angles?
One angle of an isosceles triangle has measure 
An isosceles triangle not only has two sides of equal measure, it has two angles of equal measure. This means one of two things, which we examine separately:
Case 1: It has another  angle. This is impossible, since a triangle cannot have two obtuse angles.
angle. This is impossible, since a triangle cannot have two obtuse angles.
Case 2: Its other two angles are the ones that are of equal measure. If we let  be their common measure, then, since the sum of the measures of a triangle is
be their common measure, then, since the sum of the measures of a triangle is  ,
,






Both angles measure 
An isosceles triangle not only has two sides of equal measure, it has two angles of equal measure. This means one of two things, which we examine separately:
Case 1: It has another 
Case 2: Its other two angles are the ones that are of equal measure. If we let 

Both angles measure
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
What is the measure of angle 

Note: Figure NOT drawn to scale.
What is the measure of angle
The two angles at bottom are marked as congruent. One forms a linear pair with a  angle, so it is supplementary to that angle, making its measure
angle, so it is supplementary to that angle, making its measure  . Therefore, each marked angle measures
. Therefore, each marked angle measures  .
.
The sum of the measures of the interior angles of a triangle is  , so:
, so:




The two angles at bottom are marked as congruent. One forms a linear pair with a 


The sum of the measures of the interior angles of a triangle is 
Compare your answer with the correct one above
The angles of a triangle measure  . Evaluate
. Evaluate  .
.
The angles of a triangle measure 

The sum of the degree measures of the angles of a triangle is 180, so we solve for  in the following equation:
in the following equation:






The sum of the degree measures of the angles of a triangle is 180, so we solve for 
Compare your answer with the correct one above
The acute angles of a right triangle measure  and
and  .
.
Evaluate  .
.
The acute angles of a right triangle measure 

Evaluate 
The degree measures of the acute angles of a right triangle total 90, so we solve for  in the following equation:
in the following equation:






The degree measures of the acute angles of a right triangle total 90, so we solve for 
Compare your answer with the correct one above

Note: Figure NOT drawn to scale
Refer to the above figure.  ;
;  .
.
What is the measure of  ?
?

Note: Figure NOT drawn to scale
Refer to the above figure. 

What is the measure of 
Congruent chords of a circle have congruent minor arcs, so since  ,
,  , and their common measure is
, and their common measure is  .
.
Since there are  in a circle,
in a circle,




The inscribed angle  intercepts this arc and therefore has one-half its degree measure, which is
intercepts this arc and therefore has one-half its degree measure, which is 
Congruent chords of a circle have congruent minor arcs, so since 


Since there are 
The inscribed angle 
Compare your answer with the correct one above
Solve for  :
:

Solve for 

The sum of the internal angles of a triangle is equal to  . Therefore:
. Therefore:




The sum of the internal angles of a triangle is equal to 
Compare your answer with the correct one above

Figure NOT drawn to scale.
Refer to the above figure. Evaluate  .
.

Figure NOT drawn to scale.
Refer to the above figure. Evaluate 
The measure of an exterior angle of a triangle, which here is  , is equal to the sum of the measures of its remote interior angles, which here are
, is equal to the sum of the measures of its remote interior angles, which here are  and
and  . Consequently,
. Consequently,









 and
and  form a linear pair and, therefore,
form a linear pair and, therefore,
 .
.
The measure of an exterior angle of a triangle, which here is 





Compare your answer with the correct one above

Refer to the above figure. Express  in terms of
in terms of  .
.

Refer to the above figure. Express 

The measure of an interior angle of a triangle is equal to 180 degrees minus that of its adjacent exterior angle, so

and
 .
.
The sum of the degree measures of the three interior angles is 180, so






The measure of an interior angle of a triangle is equal to 180 degrees minus that of its adjacent exterior angle, so
and

The sum of the degree measures of the three interior angles is 180, so
Compare your answer with the correct one above

In the above figure,  .
.
Give the measure of  .
.

In the above figure, 
Give the measure of 
 and
and  form a linear pair, so their degree measures total
form a linear pair, so their degree measures total  ; consequently,
; consequently,



 , so by the Isosceles Triangle Theorem,
, so by the Isosceles Triangle Theorem,

The sum of the degree measures of a triangle is  , so
, so








The sum of the degree measures of a triangle is 
Compare your answer with the correct one above
Which of the following is true about a triangle with two angles that measure  and
and  ?
?
Which of the following is true about a triangle with two angles that measure 

A triangle must have at least two acute angles; however, a triangle with angles that measure  and
and  could have at most one acute angle, an impossible situation. Therefore, this triangle is nonexistent.
could have at most one acute angle, an impossible situation. Therefore, this triangle is nonexistent.
A triangle must have at least two acute angles; however, a triangle with angles that measure 

Compare your answer with the correct one above

 is a right angle;
is a right angle;  ,
,  .
.
Which is the greater quantity?
(a) 
(b) 



Which is the greater quantity?
(a)
(b)
 . Corresponding angles of similar triangles are congruent, so since
. Corresponding angles of similar triangles are congruent, so since  is a right angle, so is
is a right angle, so is  .
.
The hypotenuse  of
of  is twice as long as leg
is twice as long as leg  ; by the
; by the  Theorem,
Theorem, 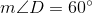 . Again, by similiarity,
. Again, by similiarity,
 .
.



The hypotenuse 



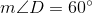

Compare your answer with the correct one above

NOTE: Figures NOT drawn to scale.
Refer to the above two triangles.

What is  ?
?

NOTE: Figures NOT drawn to scale.
Refer to the above two triangles.
What is 
Corresponding sides of similar triangle are proportional, so if
 , then
, then

Substitute the known sidelengths, then solve for  :
:




Corresponding sides of similar triangle are proportional, so if

Substitute the known sidelengths, then solve for 
Compare your answer with the correct one above


What is the perimeter of  ?
?
What is the perimeter of 
By definition, since,  , side lengths are in proportion.
, side lengths are in proportion.
So,








The perimeter of  is
is
 .
.
By definition, since, 
So,
The perimeter of 

Compare your answer with the correct one above


What is  ?
?
What is 
By definition, since  , all side lengths are in proportion.
, all side lengths are in proportion.




By definition, since 
Compare your answer with the correct one above
One angle of a right triangle measures 45 degrees, and the hypotenuse measures 8 centimeters. Give the area of the triangle.
One angle of a right triangle measures 45 degrees, and the hypotenuse measures 8 centimeters. Give the area of the triangle.
This triangle has two angles of 45 and 90 degrees, so the third angle must measure 45 degrees; this is therefore an isosceles right triangle.
By the Pythagorean Theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let  hypotenuse and
hypotenuse and  side length.
side length.


We can then plug this side length into the formula for area.

This triangle has two angles of 45 and 90 degrees, so the third angle must measure 45 degrees; this is therefore an isosceles right triangle.
By the Pythagorean Theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let 

We can then plug this side length into the formula for area.
Compare your answer with the correct one above