Quadrilaterals - ISEE Upper Level Mathematics Achievement
Card 0 of 20
Solve for 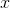 :
:

Solve for 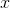

Find the sum of the interior angles of the polygon using the following equation where n is equal to the number of sides.


The sum of the angles must equal 360.




Find the sum of the interior angles of the polygon using the following equation where n is equal to the number of sides.
The sum of the angles must equal 360.
Compare your answer with the correct one above
Consider the rhombus below. Solve for 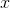 .
.

Consider the rhombus below. Solve for 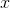

The total sum of the interior angles of a quadrilateral is  degrees. In this problem, we are only considering half of the interior angles:
degrees. In this problem, we are only considering half of the interior angles:



The total sum of the interior angles of a quadrilateral is 
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
The above depicts a rhombus and one of its diagonals. What is 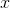 ?
?

Note: Figure NOT drawn to scale.
The above depicts a rhombus and one of its diagonals. What is 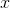
The diagonals of a rhombus bisect the angles.
The angle bisected must be supplementary to the  angle since they are consecutive angles of a parallelogram; therefore, that angle has measure
angle since they are consecutive angles of a parallelogram; therefore, that angle has measure 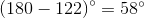 , and
, and  is half that, or
is half that, or 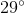 .
.
The diagonals of a rhombus bisect the angles.
The angle bisected must be supplementary to the 
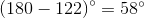

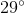
Compare your answer with the correct one above
Three of the interior angles of a quadrilateral measure  ,
,  , and
, and  . What is the measure of the fourth interior angle?
. What is the measure of the fourth interior angle?
Three of the interior angles of a quadrilateral measure 


The measures of the angles of a quadrilateral have sum  . If
. If  is the measure of the unknown angle, then:
is the measure of the unknown angle, then:




The angle measures  .
.
The measures of the angles of a quadrilateral have sum 

The angle measures 
Compare your answer with the correct one above
The angles of a quadrilateral measure  . Evaluate
. Evaluate  .
.
The angles of a quadrilateral measure 

The sum of the degree measures of the angles of a quadrilateral is 360, so we can set up and solve for  in the equation:
in the equation:






The sum of the degree measures of the angles of a quadrilateral is 360, so we can set up and solve for 
Compare your answer with the correct one above
The four angles of a quadrilateral have the following value: 79 degrees, 100 degrees, 50 degrees, and  degrees. What is the value of
degrees. What is the value of  ?
?
The four angles of a quadrilateral have the following value: 79 degrees, 100 degrees, 50 degrees, and 

Given that there are 360 degrees when all the angles of a quadrilateral are added toghether, this problem can be solved with the following equation:




Given that there are 360 degrees when all the angles of a quadrilateral are added toghether, this problem can be solved with the following equation:
Compare your answer with the correct one above
In a quadrilateral, the angles have the following values:
 .
.
What is the value of  ?
?
In a quadrilateral, the angles have the following values:

What is the value of 
Given that there are 360 degrees when the angles of a quadrilateral are added together, it follows that:




Given that there are 360 degrees when the angles of a quadrilateral are added together, it follows that:
Compare your answer with the correct one above
Cassie is making a kite for her little brother. She has two plastic tubes to use as the skeleton, measuring  inches and
inches and  inches. If these two tubes represent the diagnals of the kite, how many square inches of paper will she need to make the kite?
inches. If these two tubes represent the diagnals of the kite, how many square inches of paper will she need to make the kite?
Cassie is making a kite for her little brother. She has two plastic tubes to use as the skeleton, measuring 

To find the area of a kite, use the formula  , where
, where  represents one diagnal and
represents one diagnal and  represents the other.
represents the other.
Since Cassie has one tube measuring  inches, we can substitute
inches, we can substitute  for
for  . We can also substitute the other tube that measures
. We can also substitute the other tube that measures  inches in for
inches in for  .
.

To find the area of a kite, use the formula 


Since Cassie has one tube measuring 




Compare your answer with the correct one above
Two diagonals of a kite have the lengths of  and
and  . Give the area of the kite.
. Give the area of the kite.
Two diagonals of a kite have the lengths of 

The area of a kite is half the product of the diagonals, i.e.
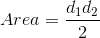 ,
,
where  and
and  are the lengths of the diagonals.
are the lengths of the diagonals.

The area of a kite is half the product of the diagonals, i.e.
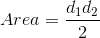
where 

Compare your answer with the correct one above
In the following kite,  ,
,  and
and  . Give the area of the kite. Figure not drawn to scale.
. Give the area of the kite. Figure not drawn to scale.

In the following kite, 



When you know the length of two unequal sides of a kite and their included angle, the following formula can be used to find the area of a kite:
 ,
,
where _ _are the lengths of two unequal sides,
_are the lengths of two unequal sides,  is the angle between them and
is the angle between them and  is the sine function.
is the sine function.

When you know the length of two unequal sides of a kite and their included angle, the following formula can be used to find the area of a kite:

where _


Compare your answer with the correct one above
Find the area of a kite with one diagonal having length 18in and the other diagonal having a length that is half the first diagonal.
Find the area of a kite with one diagonal having length 18in and the other diagonal having a length that is half the first diagonal.
To find the area of a kite, we will use the following formula:

where p and q are the lengths of the diagonals of the kite.
Now, we know the length of one diagonal is 18in. We also know the other diagonal is half of the first diagonal. Therefore, the second diagonal has a length of 9in.
Knowing this, we can substitute into the formula. We get



To find the area of a kite, we will use the following formula:
where p and q are the lengths of the diagonals of the kite.
Now, we know the length of one diagonal is 18in. We also know the other diagonal is half of the first diagonal. Therefore, the second diagonal has a length of 9in.
Knowing this, we can substitute into the formula. We get
Compare your answer with the correct one above

Give the area of the above parallelogram if  .
.

Give the area of the above parallelogram if 
Multiply height  by base
by base  to get the area.
to get the area.
By the 30-60-90 Theorem:

and

The area is therefore

Multiply height 

By the 30-60-90 Theorem:
and
The area is therefore
Compare your answer with the correct one above

Give the area of the above parallelogram if  .
.

Give the area of the above parallelogram if 
Multiply height  by base
by base  to get the area.
to get the area.
By the 45-45-90 Theorem,
 .
.
The area is therefore

Multiply height 

By the 45-45-90 Theorem,

The area is therefore
Compare your answer with the correct one above
Three of the vertices of a parallelogram on the coordinate plane are  . What is the area of the parallelogram?
. What is the area of the parallelogram?
Three of the vertices of a parallelogram on the coordinate plane are 
As can be seen in the diagram, there are three possible locations of the fourth point of the parallelogram:

Regardless of the location of the fourth point, however, the triangle with the given three vertices comprises exactly half the parallelogram. Therefore, the parallelogram has double that of the triangle.
The area of the triangle can be computed by noting that the triangle is actually a part of a 12-by-12 square with three additional right triangles cut out:

The area of the 12 by 12 square is 
The area of the green triangle is  .
.
The area of the blue triangle is  .
.
The area of the pink triangle is  .
.
The area of the main triangle is therefore

The parallelogram has area twice this, or  .
.
As can be seen in the diagram, there are three possible locations of the fourth point of the parallelogram:

Regardless of the location of the fourth point, however, the triangle with the given three vertices comprises exactly half the parallelogram. Therefore, the parallelogram has double that of the triangle.
The area of the triangle can be computed by noting that the triangle is actually a part of a 12-by-12 square with three additional right triangles cut out:

The area of the 12 by 12 square is
The area of the green triangle is 
The area of the blue triangle is 
The area of the pink triangle is 
The area of the main triangle is therefore
The parallelogram has area twice this, or 
Compare your answer with the correct one above
One of the sides of a square on the coordinate plane has an endpoint at the point with coordinates  ; it has the origin as its other endpoint. What is the area of this square?
; it has the origin as its other endpoint. What is the area of this square?
One of the sides of a square on the coordinate plane has an endpoint at the point with coordinates 
The length of a segment with endpoints  and
and  can be found using the distance formula with
can be found using the distance formula with  ,
,  ,
,  :
:





This is the length of one side of the square, so the area is the square of this, or 41.
The length of a segment with endpoints 




This is the length of one side of the square, so the area is the square of this, or 41.
Compare your answer with the correct one above
A rectangle and a square have the same perimeter. The area of the square is  square centimeters; the length of the rectangle is
square centimeters; the length of the rectangle is  centimeters. Give the width of the rectangle in centimeters.
centimeters. Give the width of the rectangle in centimeters.
A rectangle and a square have the same perimeter. The area of the square is 

The sidelength of a square with area  square centimeters is
square centimeters is  centimeters; its perimeter, as well as that of the rectangle, is therefore
centimeters; its perimeter, as well as that of the rectangle, is therefore  centimeters.
centimeters.
Using the formula for the perimeter of a rectangle, substitute  and solve for
and solve for  as follows:
as follows:







The sidelength of a square with area 


Using the formula for the perimeter of a rectangle, substitute 

Compare your answer with the correct one above
A rectangle on the coordinate plane has its vertices at the points  .
.
What percent of the rectangle is located in Quadrant I?
A rectangle on the coordinate plane has its vertices at the points 
What percent of the rectangle is located in Quadrant I?
The total area of the rectangle is
![\left [ 3- (-6) \right ] \times\left [ 4- (-2) \right ] = 9 \times 6 = 54](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/146123/gif.latex) .
.
The area of the portion of the rectangle in Quadrant I is
 .
.
Therefore, the portion of the rectangle in Quadrant I is
 .
.
The total area of the rectangle is
![\left [ 3- (-6) \right ] \times\left [ 4- (-2) \right ] = 9 \times 6 = 54](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/146123/gif.latex)
The area of the portion of the rectangle in Quadrant I is

Therefore, the portion of the rectangle in Quadrant I is

Compare your answer with the correct one above
In a rectangle, the width is  while the length is
while the length is  . If
. If  , what is the area of the rectangle?
, what is the area of the rectangle?
In a rectangle, the width is 


In a rectangle in which the width is x while the length is 4x, the first step is to solve for x. If  , the value of x can be found by dividing each side of this equation by 3.
, the value of x can be found by dividing each side of this equation by 3.
Doing so gives us the information that x is equal to 3.
Thus, the area is equal to:



In a rectangle in which the width is x while the length is 4x, the first step is to solve for x. If 
Doing so gives us the information that x is equal to 3.
Thus, the area is equal to:
Compare your answer with the correct one above
Your geometry book has a rectangular front cover which is 12 inches by 8 inches.
What is the area of your book cover?
Your geometry book has a rectangular front cover which is 12 inches by 8 inches.
What is the area of your book cover?
Your geometry book has a rectangular front cover which is 12 inches by 8 inches.
What is the area of your book cover?
To find the area of a rectangle, use the following formula:

Plug in our knowns and solve:

Your geometry book has a rectangular front cover which is 12 inches by 8 inches.
What is the area of your book cover?
To find the area of a rectangle, use the following formula:
Plug in our knowns and solve:
Compare your answer with the correct one above
Find the area of a rectangle with a width of 5in and a length that is three times the width.
Find the area of a rectangle with a width of 5in and a length that is three times the width.
To find the area of a rectangle, we will use the following formula:

where l is the length and w is the width of the rectangle.
Now, we know the width of the rectangle is 5in. We also know the length is three times the width. Therefore, the length is 15in.
Knowing this, we can substitute into the formula. We get


To find the area of a rectangle, we will use the following formula:
where l is the length and w is the width of the rectangle.
Now, we know the width of the rectangle is 5in. We also know the length is three times the width. Therefore, the length is 15in.
Knowing this, we can substitute into the formula. We get
Compare your answer with the correct one above