Geometry - ISEE Upper Level Mathematics Achievement
Card 0 of 20
Find the distance between  and
and  .
.
Find the distance between 

To find the distance, first remember the distance formula:  . Plug in so that you have:
. Plug in so that you have:  . Simplify so that you get
. Simplify so that you get  . This yields
. This yields  .
.
To find the distance, first remember the distance formula: 



Compare your answer with the correct one above

Examine the above diagram. If  , give
, give  in terms of
in terms of  .
.

Examine the above diagram. If 


The two marked angles are same-side exterior angles of parallel lines, which are supplementary - that is, their measures have sum 180. We can solve for  in this equation:
in this equation:





The two marked angles are same-side exterior angles of parallel lines, which are supplementary - that is, their measures have sum 180. We can solve for 
Compare your answer with the correct one above

Examine the above diagram. If  , give
, give  in terms of
in terms of  .
.

Examine the above diagram. If 


The two marked angles are same-side interior angles of parallel lines, which are supplementary - that is, their measures have sum 180. We can solve for  in this equation:
in this equation:







The two marked angles are same-side interior angles of parallel lines, which are supplementary - that is, their measures have sum 180. We can solve for 
Compare your answer with the correct one above

Examine the above diagram. Which of the following statements must be true whether or not  and
and  are parallel?
are parallel?

Examine the above diagram. Which of the following statements must be true whether or not 

Four statements can be eliminated by the various parallel theorems and postulates. Congruence of alternate interior angles or corresponding angles forces the lines to be parallel, so
 and
and
 .
.
Also, if same-side interior angles or same-side exterior angles are supplementary, the lines are parallel, so
 and
and
 .
.
However,  whether or not
whether or not  since they are vertical angles, which are always congruent.
since they are vertical angles, which are always congruent.
Four statements can be eliminated by the various parallel theorems and postulates. Congruence of alternate interior angles or corresponding angles forces the lines to be parallel, so


Also, if same-side interior angles or same-side exterior angles are supplementary, the lines are parallel, so


However, 

Compare your answer with the correct one above

Examine the above diagram. What is  ?
?

Examine the above diagram. What is 
By angle addition,






By angle addition,
Compare your answer with the correct one above
 and
and  are supplementary;
are supplementary;  and
and  are complementary.
are complementary.
 .
.
What is  ?
?





What is 
Supplementary angles and complementary angles have measures totaling  and
and  , respectively.
, respectively.
 , so its supplement
, so its supplement  has measure
has measure

 , the complement of
, the complement of  , has measure
, has measure

Supplementary angles and complementary angles have measures totaling 





Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
In the above figure,  and
and  . Which of the following is equal to
. Which of the following is equal to  ?
?

Note: Figure NOT drawn to scale.
In the above figure, 


 and
and  form a linear pair, so their angle measures total
form a linear pair, so their angle measures total  . Set up and solve the following equation:
. Set up and solve the following equation:









Compare your answer with the correct one above
Two angles which form a linear pair have measures  and
and  . Which is the lesser of the measures (or the common measure) of the two angles?
. Which is the lesser of the measures (or the common measure) of the two angles?
Two angles which form a linear pair have measures 

Two angles that form a linear pair are supplementary - that is, they have measures that total  . Therefore, we set and solve for
. Therefore, we set and solve for  in this equation:
in this equation:




The two angles have measure

and

 is the lesser of the two measures and is the correct choice.
is the lesser of the two measures and is the correct choice.
Two angles that form a linear pair are supplementary - that is, they have measures that total 

The two angles have measure
and

Compare your answer with the correct one above
Two vertical angles have measures  and
and  . Which is the lesser of the measures (or the common measure) of the two angles?
. Which is the lesser of the measures (or the common measure) of the two angles?
Two vertical angles have measures 

Two vertical angles - angles which share a vertex and whose union is a pair of lines - have the same measure. Therefore, we set up and solve the equation





Two vertical angles - angles which share a vertex and whose union is a pair of lines - have the same measure. Therefore, we set up and solve the equation
Compare your answer with the correct one above
A line  intersects parallel lines
intersects parallel lines  and
and  .
.  and
and  are corresponding angles;
are corresponding angles;  and
and  are same side interior angles.
are same side interior angles.



Evaluate  .
.
A line 






Evaluate 
When a transversal such as  crosses two parallel lines, two corresponding angles - angles in the same relative position to their respective lines - are congruent. Therefore,
crosses two parallel lines, two corresponding angles - angles in the same relative position to their respective lines - are congruent. Therefore,



Two same-side interior angles are supplementary - that is, their angle measures total 180 - so



We can solve this system by the substitution method as follows:





Backsolve:


 , which is the correct response.
, which is the correct response.
When a transversal such as 
Two same-side interior angles are supplementary - that is, their angle measures total 180 - so
We can solve this system by the substitution method as follows:
Backsolve:

Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
Refer to the above diagram. Give the measure of  .
.

Note: Figure NOT drawn to scale.
Refer to the above diagram. Give the measure of 
The top and bottom angles, being vertical angles - angles which share a vertex and whose union is a pair of lines - have the same measure, so
 ,
,
or, simplified,


The right and bottom angles form a linear pair, so their degree measures total 180. That is,

Substitute  for
for  :
:




The left and right angles, being vertical angles, have the same measure, so, since the right angle measures  , this is also the measure of the left angle,
, this is also the measure of the left angle,  .
.
The top and bottom angles, being vertical angles - angles which share a vertex and whose union is a pair of lines - have the same measure, so

or, simplified,
The right and bottom angles form a linear pair, so their degree measures total 180. That is,
Substitute 

The left and right angles, being vertical angles, have the same measure, so, since the right angle measures 

Compare your answer with the correct one above

Figure NOT drawn to scale
The above figure shows Trapezoid  , with
, with  and
and  tangent to the circle.
tangent to the circle.  ; evaluate
; evaluate  .
.

Figure NOT drawn to scale
The above figure shows Trapezoid 




By the Same-Side Interior Angle Theorem, since  ,
,  and
and  are supplementary - that is, their degree measures total
are supplementary - that is, their degree measures total  . Therefore,
. Therefore,



 is an inscribed angle, so the arc it intercepts,
is an inscribed angle, so the arc it intercepts,  , has twice its degree measure;
, has twice its degree measure;
 .
.
The corresponding major arc,  , has as its measure
, has as its measure

The measure of an angle formed by two tangents to a circle is equal to half the difference of those of its intercepted arcs:


Again, by the Same-Side Interior Angles Theorem,  and
and  are supplementary, so
are supplementary, so



By the Same-Side Interior Angle Theorem, since 






The corresponding major arc, 
The measure of an angle formed by two tangents to a circle is equal to half the difference of those of its intercepted arcs:
Again, by the Same-Side Interior Angles Theorem, 

Compare your answer with the correct one above
If the sum of 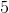 angles in a hexagon is equal to
angles in a hexagon is equal to 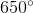 , what is the value of the remaining sixth angle?
, what is the value of the remaining sixth angle?
If the sum of 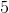
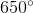
The sum of the angles in a polygon can be found using the equation below, in which t is equal to the total sum of the angles, and n is equal to the number of sides.

Given that a hexagon has 6 angles, the total number of angles will be:



Given that 5 of the angles have a sum of 650 degrees, we would subtract 650 from 720, resulting in 70 degrees.
The sum of the angles in a polygon can be found using the equation below, in which t is equal to the total sum of the angles, and n is equal to the number of sides.
Given that a hexagon has 6 angles, the total number of angles will be:
Given that 5 of the angles have a sum of 650 degrees, we would subtract 650 from 720, resulting in 70 degrees.
Compare your answer with the correct one above
Solve for 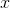 :
:

Solve for 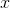

Find the sum of the interior angles of the polygon using the following equation where n is equal to the number of sides.


The sum of the angles must equal 360.




Find the sum of the interior angles of the polygon using the following equation where n is equal to the number of sides.
The sum of the angles must equal 360.
Compare your answer with the correct one above
The measures of the angles of a pentagon are  . If
. If  , what is
, what is  ?
?
The measures of the angles of a pentagon are 


The angles of a pentagon measure a total of  . From the information, we know that:
. From the information, we know that:


If  , then
, then






The angles of a pentagon measure a total of 
If 
Compare your answer with the correct one above
A convex pentagon has four angles that measure  each. What is the measure of the fifth angle?
each. What is the measure of the fifth angle?
A convex pentagon has four angles that measure 
The angles of a pentagon measure a total of  . If we let the unknown angle measure be
. If we let the unknown angle measure be  , then from this information:
, then from this information:




Since an angle measure cannot be negative, this pentagon cannot exist.
The angles of a pentagon measure a total of 

Since an angle measure cannot be negative, this pentagon cannot exist.
Compare your answer with the correct one above
The measures of the angles of a pentagon are  . If
. If  , what is
, what is  ?
?
The measures of the angles of a pentagon are 


The angles of a pentagon measure a total of  . From the information, we know:
. From the information, we know:


If  , then the above becomes:
, then the above becomes:






The angles of a pentagon measure a total of 
If 
Compare your answer with the correct one above
Solve for  :
:

Solve for 

The sum of the interior angles of a pentagon can be determined by the following equation, where  is the number of sides:
is the number of sides:

Therefore:




The sum of the interior angles of a pentagon can be determined by the following equation, where 
Therefore:
Compare your answer with the correct one above
Consider the rhombus below. Solve for 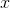 .
.

Consider the rhombus below. Solve for 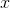

The total sum of the interior angles of a quadrilateral is  degrees. In this problem, we are only considering half of the interior angles:
degrees. In this problem, we are only considering half of the interior angles:



The total sum of the interior angles of a quadrilateral is 
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
The above depicts a rhombus and one of its diagonals. What is 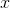 ?
?

Note: Figure NOT drawn to scale.
The above depicts a rhombus and one of its diagonals. What is 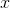
The diagonals of a rhombus bisect the angles.
The angle bisected must be supplementary to the  angle since they are consecutive angles of a parallelogram; therefore, that angle has measure
angle since they are consecutive angles of a parallelogram; therefore, that angle has measure 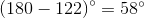 , and
, and  is half that, or
is half that, or 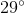 .
.
The diagonals of a rhombus bisect the angles.
The angle bisected must be supplementary to the 
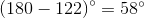

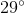
Compare your answer with the correct one above