How to find the area of a trapezoid - ISEE Middle Level Math
Card 0 of 9
A trapezoid has a height of  inches and bases measuring
inches and bases measuring  inches and
inches and  inches. What is its area?
inches. What is its area?
A trapezoid has a height of 


Use the following formula, with  :
:
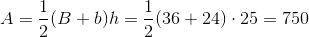
Use the following formula, with 
Compare your answer with the correct one above
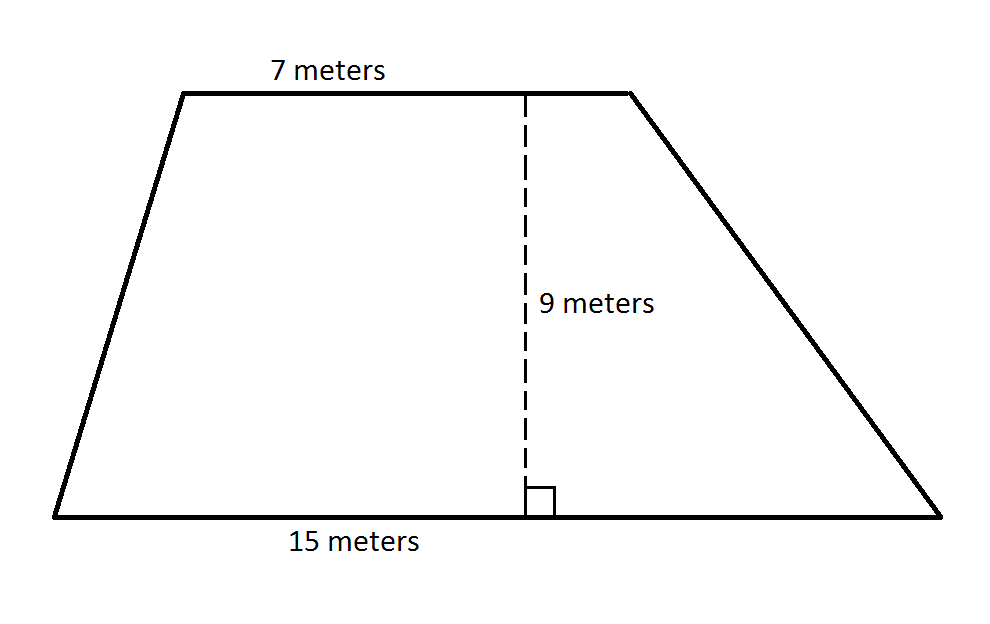
What is the area of the trapezoid?

What is the area of the trapezoid?
To find the area of a trapezoid, multiply the sum of the bases (the parallel sides) by the height (the perpendicular distance between the bases), and then divide by 2.
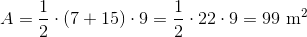
To find the area of a trapezoid, multiply the sum of the bases (the parallel sides) by the height (the perpendicular distance between the bases), and then divide by 2.
Compare your answer with the correct one above
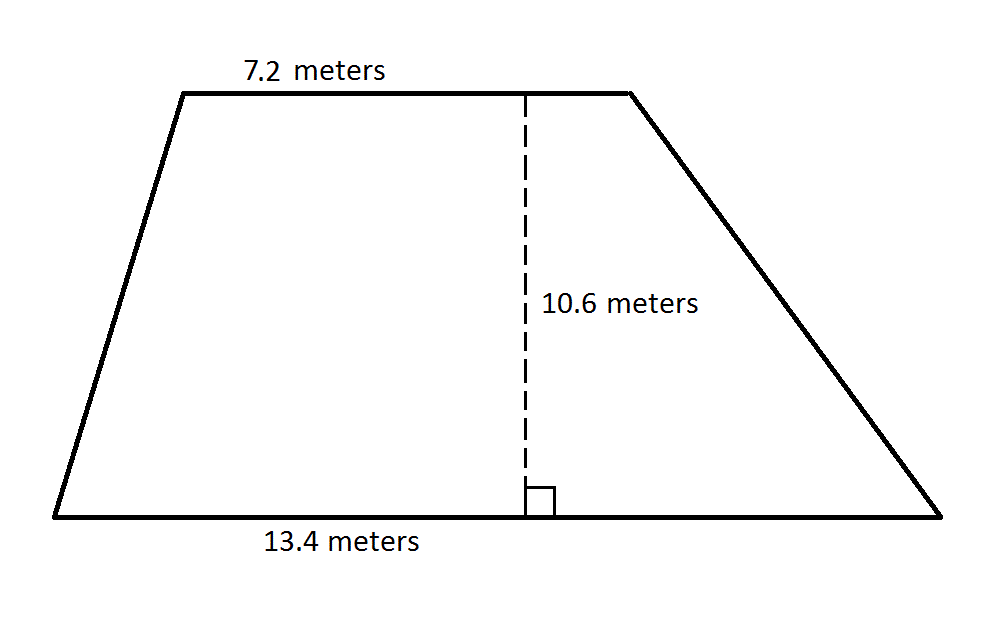
What is the area of the above trapezoid?

What is the area of the above trapezoid?
To find the area of a trapezoid, multiply one half (or 0.5, since we are working with decimals) by the sum of the lengths of its bases (the parallel sides) by its height (the perpendicular distance between the bases). This quantity is
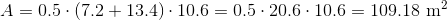
To find the area of a trapezoid, multiply one half (or 0.5, since we are working with decimals) by the sum of the lengths of its bases (the parallel sides) by its height (the perpendicular distance between the bases). This quantity is
Compare your answer with the correct one above
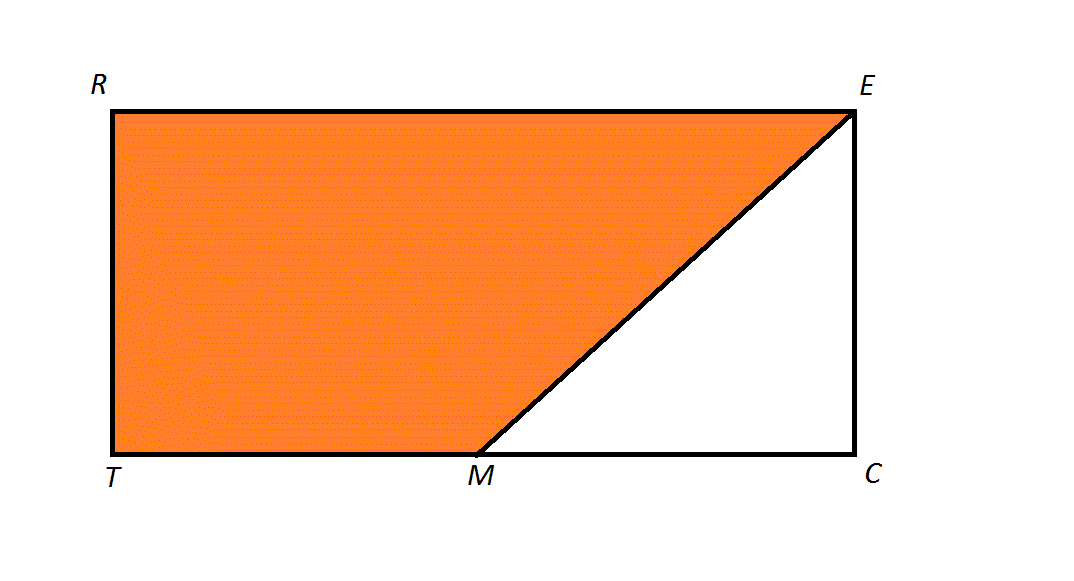
The above diagram depicts a rectangle  with isosceles triangle
with isosceles triangle  . If
. If  is the midpoint of
is the midpoint of  , and the area of the orange region is
, and the area of the orange region is  , then what is the length of one leg of
, then what is the length of one leg of  ?
?

The above diagram depicts a rectangle 





The length of a leg of  is equal to the height of the orange region, which is a trapezoid. Call this length/height
is equal to the height of the orange region, which is a trapezoid. Call this length/height  .
.
Since the triangle is isosceles, then  , and since
, and since  is the midpoint of
is the midpoint of  ,
,  . Also, since opposite sides of a rectangle are congruent,
. Also, since opposite sides of a rectangle are congruent,
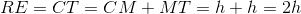
Therefore, the orange region is a trapezoid with bases  and
and  and height
and height  . Its area is 72, so we can set up and solve this equation using the area formula for a trapezoid:
. Its area is 72, so we can set up and solve this equation using the area formula for a trapezoid:
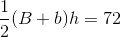
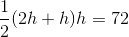
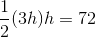
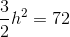
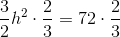
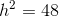
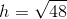
This is the length of one leg of the triangle.
The length of a leg of 

Since the triangle is isosceles, then 



Therefore, the orange region is a trapezoid with bases 


This is the length of one leg of the triangle.
Compare your answer with the correct one above
Find the area of the trapezoid:
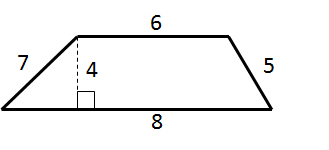
Find the area of the trapezoid:

The area of a trapezoid can be determined using the equation  .
.
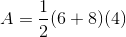
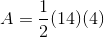
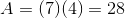
The area of a trapezoid can be determined using the equation 
Compare your answer with the correct one above
Find the area of a trapezoid with bases equal to 7 and 9 and height is 2.
Find the area of a trapezoid with bases equal to 7 and 9 and height is 2.
To solve, simply use the formula for the area of a trapezoid.
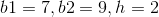
Thus,
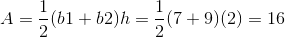
To solve, simply use the formula for the area of a trapezoid.
Thus,
Compare your answer with the correct one above
Find the area of a trapezoid with bases of 10 centimeters and 8 centimeters, and a height of 4 centimeters.
Find the area of a trapezoid with bases of 10 centimeters and 8 centimeters, and a height of 4 centimeters.
The formula for area of a trapezoid is:
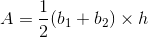
where
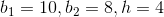
therefore the area equation becomes,
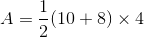
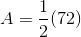
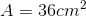
The formula for area of a trapezoid is:
where
therefore the area equation becomes,
Compare your answer with the correct one above
You recently bought a new bookshelf with a base in the shape of an isosceles trapezoid. If the small base is 2 feet, the large base is 3 feet, and the depth is 8 inches, what is the area of the base of your new bookshelf?
You recently bought a new bookshelf with a base in the shape of an isosceles trapezoid. If the small base is 2 feet, the large base is 3 feet, and the depth is 8 inches, what is the area of the base of your new bookshelf?
You recently bought a new bookshelf with a base in the shape of an isosceles trapezoid. If the small base is 2 feet, the large base is 3 feet, and the depth is 8 inches, what is the area of the base of your new bookshelf?
To find the area of a trapezoid, we need to use the following formula:
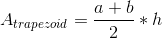
Where a and b are the lengths of the bases, and h is the perpendicular distance from one base to another.
We are given a and b, and then h will be the same as our depth. The tricky part is realizing that our depth is in inches, while our base lengths are in feet. We need to convert 8 inches to feet:
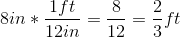
Next, plug it all into our equation up above.
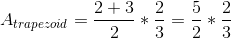
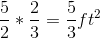
So our answer is:
You recently bought a new bookshelf with a base in the shape of an isosceles trapezoid. If the small base is 2 feet, the large base is 3 feet, and the depth is 8 inches, what is the area of the base of your new bookshelf?
To find the area of a trapezoid, we need to use the following formula:
Where a and b are the lengths of the bases, and h is the perpendicular distance from one base to another.
We are given a and b, and then h will be the same as our depth. The tricky part is realizing that our depth is in inches, while our base lengths are in feet. We need to convert 8 inches to feet:
Next, plug it all into our equation up above.
So our answer is:
Compare your answer with the correct one above
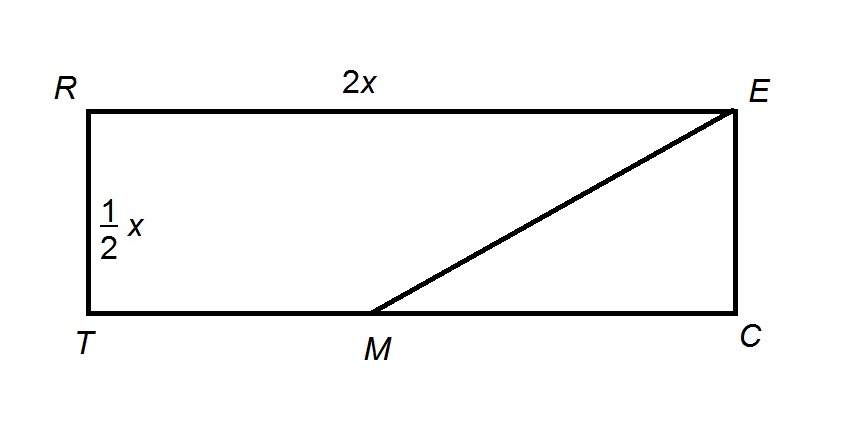
The above diagram shows Rectangle  , with midpoint
, with midpoint  of
of  .
.
The area of Quadrilateral  is
is  . Evaluate
. Evaluate  .
.

The above diagram shows Rectangle 


The area of Quadrilateral 


The easiest way to see this problem is to note that Quadrilateral  has as its area that of Rectangle
has as its area that of Rectangle  minus that of
minus that of  .
.
The area of Rectangle  is its length multiplied by its width:
is its length multiplied by its width:
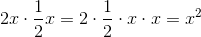
 is the midpoint of
is the midpoint of  , so
, so  has as its base and height
has as its base and height  and
and  , respectively;
, respectively;
its area is half their product, or
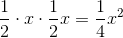
The area of Quadrilateral  is
is
 , so
, so
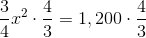
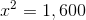
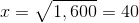
The easiest way to see this problem is to note that Quadrilateral 


The area of Rectangle 





its area is half their product, or
The area of Quadrilateral 

Compare your answer with the correct one above