Solid Geometry - Intermediate Geometry
Card 0 of 20
Find the diagonal of a cube with a side length of  .
.
Find the diagonal of a cube with a side length of 
The diagonal of a cube is simply given by:

Where  is the side length of the cube.
is the side length of the cube.
So since our 


The diagonal of a cube is simply given by:
Where 
So since our
Compare your answer with the correct one above
Find the length of a diagonal of a cube with volume of 
Find the length of a diagonal of a cube with volume of
There is a formula for the length of a cube's diagonal given the side length. However, we might not remember that formula as it is less common. However, we can also find the length using the Pythagorean Theorem.
But first, we need to find the side length. We know the volume is 64. Our formula for volume is

Substituting gives

Taking the cube root gives us a side length of 4. Now let's look at our cube.

We need to begin by finding the length of the diagonal of the bottom face of our cube (the green segment). This can be done either by using the Pythagorean Theorem or by realizing that the right triangle is in fact a 45-45-90 triangle. Either way, we realize that our diagonal (the hypotenuse) is  .
.

We now seek to find the diagonal of the cube (the blue segment). We do this by looking at the right triangle formed by it, the left vertical edge, and the face diagonal we just found. This time our only recourse is to do the Pythagorean Theorem.




In general, the formula for the diagonal of a cube with side length  is
is

The length of our diagonal is 
There is a formula for the length of a cube's diagonal given the side length. However, we might not remember that formula as it is less common. However, we can also find the length using the Pythagorean Theorem.
But first, we need to find the side length. We know the volume is 64. Our formula for volume is
Substituting gives
Taking the cube root gives us a side length of 4. Now let's look at our cube.

We need to begin by finding the length of the diagonal of the bottom face of our cube (the green segment). This can be done either by using the Pythagorean Theorem or by realizing that the right triangle is in fact a 45-45-90 triangle. Either way, we realize that our diagonal (the hypotenuse) is 

We now seek to find the diagonal of the cube (the blue segment). We do this by looking at the right triangle formed by it, the left vertical edge, and the face diagonal we just found. This time our only recourse is to do the Pythagorean Theorem.
In general, the formula for the diagonal of a cube with side length 
The length of our diagonal is
Compare your answer with the correct one above
Suppose the volume of a cube is  . What is the length of the diagonal?
. What is the length of the diagonal?
Suppose the volume of a cube is 
Write the equation for the volume of a cube. Substitute the volume to find the side length,  .
.



Write the equation for finding diagonals given an edge length for a cube.

Substitute the side length to find the diagonal length.
The answer is  .
.
Write the equation for the volume of a cube. Substitute the volume to find the side length, 
Write the equation for finding diagonals given an edge length for a cube.
Substitute the side length to find the diagonal length.
The answer is 
Compare your answer with the correct one above
If the volume of a cube was one eighth, what is the diagonal of the cube?
If the volume of a cube was one eighth, what is the diagonal of the cube?
Write the volume of a cube and substitute the given volume to find a side length.



Write the diagonal formula for a cube and substitute the side length.

Write the volume of a cube and substitute the given volume to find a side length.
Write the diagonal formula for a cube and substitute the side length.
Compare your answer with the correct one above
If the volume of a cube was  , what is the length of the diagonal?
, what is the length of the diagonal?
If the volume of a cube was 
Write the equation for finding the volume of a cube, and substitute in the volume.



Write the diagonal equation for cubes and substitute in the given length.

Write the equation for finding the volume of a cube, and substitute in the volume.
Write the diagonal equation for cubes and substitute in the given length.
Compare your answer with the correct one above
If the surface area of a cube was  , what is the length of the diagonal?
, what is the length of the diagonal?
If the surface area of a cube was 
Write the surface area formula for cubes and substitute the given area.




Write the diagonal formula for cubes and substitute the side length.

Write the surface area formula for cubes and substitute the given area.
Write the diagonal formula for cubes and substitute the side length.
Compare your answer with the correct one above
Find the distance from point A to point B in the cube below (leave answer in simplest radical form):

Find the distance from point A to point B in the cube below (leave answer in simplest radical form):

When calculating the diagonal of the cube, point A to point B.
We must first find the diagonal of the base of the cube.
The base of the cube is a square where all sides are 8.
The diagonal of this square is found either by the pythagorean theorem or by what we know about 45-45-90 triangles to get the diagonal of the base below:

The diagonal of the base would be from point A to point C in the drawing.

We can see that the diagonal of the base and side BC of the cube form the two legs of a right triangle that will allow us to find the 3D diagonal of the whole cube.
Use the pythagorean theorem with BC and the Diagonal of the Base.



Take the square root of both sides.

After simplifying everything we get the final answer for the Diagonal of the Cube (AB).

When calculating the diagonal of the cube, point A to point B.
We must first find the diagonal of the base of the cube.
The base of the cube is a square where all sides are 8.
The diagonal of this square is found either by the pythagorean theorem or by what we know about 45-45-90 triangles to get the diagonal of the base below:
The diagonal of the base would be from point A to point C in the drawing.

We can see that the diagonal of the base and side BC of the cube form the two legs of a right triangle that will allow us to find the 3D diagonal of the whole cube.
Use the pythagorean theorem with BC and the Diagonal of the Base.
Take the square root of both sides.
After simplifying everything we get the final answer for the Diagonal of the Cube (AB).
Compare your answer with the correct one above
A cube has a side length of 6 meters. What is the length of its diagonal across one of the faces?
A cube has a side length of 6 meters. What is the length of its diagonal across one of the faces?
Since all sides of a cube are equal and all sides form right angles, we use pythagorean theorem to find the length of the diagonal.



 meters
meters
Since all sides of a cube are equal and all sides form right angles, we use pythagorean theorem to find the length of the diagonal.

Compare your answer with the correct one above
What is the length of the diagonal of a rectangular box with the dimensions of  ?
?
What is the length of the diagonal of a rectangular box with the dimensions of 
To solve this problem we need an extension of the Pythagorean Theorem:

So the equation to solve becomes 
So the distance of the diagonal is  .
.
To solve this problem we need an extension of the Pythagorean Theorem:
So the equation to solve becomes
So the distance of the diagonal is 
Compare your answer with the correct one above
Find the diagonal of the prism. The diagonal is represented by the dashed line.

Find the diagonal of the prism. The diagonal is represented by the dashed line.
The length of the diagonal is from the bottom left hand corner closest to us to the top right hand corner that's farthest away from us.
This kind of a problem may seem to be a little more complicated than it really is.
In order to solve for the diagonal length, all that's required is the Pythagorean Theorem. This equation will be used twice to solve for the dashed line.
For the first step of this problem, it's helpful to imagine a triangle "slice" that's being taken inside the prism.
 , where the diagonal of interest is D2, and D1 is the diagonal that cuts from corner to corner of the bottom face of the prism. Of this triangle that's outlined in pink dashed lines, the given information (the dimensions of the prism) provides a length for one of the legs (16).
, where the diagonal of interest is D2, and D1 is the diagonal that cuts from corner to corner of the bottom face of the prism. Of this triangle that's outlined in pink dashed lines, the given information (the dimensions of the prism) provides a length for one of the legs (16).
We can already "map out" that D2 (the hypotenuse of the dashed triangle) can be solved by using the Pythagorean Theorem if we can obtain the length of the other leg (D1).
The next step of this problem is to solve for D1. This will be the first use of the Pythagorean theorem. D1 is the diagonal of the base and is limited to a 2D face. This can be represented as:

The hypotenuse of the base, or the mystery length leg of the dashed triangle, can be solved by using the Pythagorean Theorem:

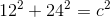





Now that we calculated the length of D1, D2 can be solved for by using the Pythagorean Theorem a second time:







The length of the diagonal is from the bottom left hand corner closest to us to the top right hand corner that's farthest away from us.
This kind of a problem may seem to be a little more complicated than it really is.
In order to solve for the diagonal length, all that's required is the Pythagorean Theorem. This equation will be used twice to solve for the dashed line.
For the first step of this problem, it's helpful to imagine a triangle "slice" that's being taken inside the prism.

We can already "map out" that D2 (the hypotenuse of the dashed triangle) can be solved by using the Pythagorean Theorem if we can obtain the length of the other leg (D1).
The next step of this problem is to solve for D1. This will be the first use of the Pythagorean theorem. D1 is the diagonal of the base and is limited to a 2D face. This can be represented as:
The hypotenuse of the base, or the mystery length leg of the dashed triangle, can be solved by using the Pythagorean Theorem:
Now that we calculated the length of D1, D2 can be solved for by using the Pythagorean Theorem a second time:
Compare your answer with the correct one above
A right rectangular prism has a width of  cm, a length of
cm, a length of  cm, and a height of
cm, and a height of  cm. Find the diagonal distance of the prism.
cm. Find the diagonal distance of the prism.
A right rectangular prism has a width of 


To find the diagonal distance of a prism, you can use the formula:
 , where
, where  = height;
= height;  = width, and
= width, and  = length.
= length.
So, in this problem
 .
.
To find the diagonal distance of a prism, you can use the formula:




So, in this problem

Compare your answer with the correct one above
A right rectangular prism has a height of  ft, a width of
ft, a width of  feet and a length that is twice its width. The volume of the prism is
feet and a length that is twice its width. The volume of the prism is  cubic feet. What is the diagonal of the prism?
cubic feet. What is the diagonal of the prism?
A right rectangular prism has a height of 


First, given the volume, you need to find the width and length. The volume of a right, rectangular prism can be found using
 , so
, so  , where
, where  represents the length and
represents the length and  represents the width.
represents the width.
Solving for  , you get
, you get

So, the width of the prism is 3 feet.
Remember that the length is twice the width, so the length is 6 feet.
Now you may use the formula for finding the diagonal:
 . So,
. So,  .
.
First, given the volume, you need to find the width and length. The volume of a right, rectangular prism can be found using




Solving for 
So, the width of the prism is 3 feet.
Remember that the length is twice the width, so the length is 6 feet.
Now you may use the formula for finding the diagonal:


Compare your answer with the correct one above
A right, rectangular prism has a length of  meters, width that is
meters, width that is  meters longer than the length, and a height of
meters longer than the length, and a height of  meters. The volume of the prism is
meters. The volume of the prism is  cubic meters. Find the diagonal of the prism.
cubic meters. Find the diagonal of the prism.
A right, rectangular prism has a length of 



First, use the volume formula,
 to find the missing length and width.
to find the missing length and width.




Since  cannot be a negative value is it represents a length of a prism, we know
cannot be a negative value is it represents a length of a prism, we know  . So the length is 2 meters, and therefore the width is 5 meters.
. So the length is 2 meters, and therefore the width is 5 meters.
Now you can plug in the length, width and height into the formula for finding the diagonal of the prism.
 .
.
First, use the volume formula,

Since 

Now you can plug in the length, width and height into the formula for finding the diagonal of the prism.

Compare your answer with the correct one above
A right, rectangular prism has a volume of  cubic centimeters. Its width is
cubic centimeters. Its width is  cm and its length is three times its height. Find the length of the diagonal of the prism.
cm and its length is three times its height. Find the length of the diagonal of the prism.
A right, rectangular prism has a volume of 

First, use the volume to find the missing height and length.
Since the length is three times the height, use  to represent the length and
to represent the length and  to represent the height.
to represent the height.
So,  .
.
So the height of the prism is 2 centimeters, and the length is 6 centimeters.
Use these values to now solve for the diagonal distance.
 .
.
First, use the volume to find the missing height and length.
Since the length is three times the height, use 

So, 
So the height of the prism is 2 centimeters, and the length is 6 centimeters.
Use these values to now solve for the diagonal distance.

Compare your answer with the correct one above
The surface area of a right, rectangular prism is  square inches. The height is
square inches. The height is  inches and the length is
inches and the length is  times the width. Find the diagonal distance of the prism.
times the width. Find the diagonal distance of the prism.
The surface area of a right, rectangular prism is 


Use the surface area, 280 square inches, and the formula for finding the surface area of a right, rectangular prsim  to find the missing length and width measurements.
to find the missing length and width measurements.
So,




Since  represents the length of a solid figure, we must assume
represents the length of a solid figure, we must assume  , rather than the negative value.
, rather than the negative value.
So, the width of the figure is 2 inches and the length is 10 inches.
Now, use the formula for finding the diagonal of a right, rectangular prism:
 .
.
Use the surface area, 280 square inches, and the formula for finding the surface area of a right, rectangular prsim 
So,
Since 

So, the width of the figure is 2 inches and the length is 10 inches.
Now, use the formula for finding the diagonal of a right, rectangular prism:

Compare your answer with the correct one above
A right, rectangular prism has a surface area of  square meters. Its width is twice its length, and its height is four times its length. Find the diagonal distance of the prism.
square meters. Its width is twice its length, and its height is four times its length. Find the diagonal distance of the prism.
A right, rectangular prism has a surface area of 
Use the surface area of the prism to find the missing length, width and height.


So, the prism's length is 1 meter, the width is 2 meters and the height is 4 meters.
Now you can find the diagonal distance using those values.
 .
.
Use the surface area of the prism to find the missing length, width and height.
So, the prism's length is 1 meter, the width is 2 meters and the height is 4 meters.
Now you can find the diagonal distance using those values.

Compare your answer with the correct one above

The above cube has edges of length 1. True or false: The dashed line has length  .
.

The above cube has edges of length 1. True or false: The dashed line has length 
Examine the diagram below.

 is a right triangle with legs of length
is a right triangle with legs of length  , so it is an isosceles - or 45-45-90 - right triangle. By the 45-45-90 Triangle Theorem its hypotenuse measures
, so it is an isosceles - or 45-45-90 - right triangle. By the 45-45-90 Triangle Theorem its hypotenuse measures

 is a right triangle with legs of lengths
is a right triangle with legs of lengths  and
and  , so the length of its hypotenuse is
, so the length of its hypotenuse is



 .
.
 , the diagonal in question, has length
, the diagonal in question, has length  , not
, not  .
.
Examine the diagram below.










Compare your answer with the correct one above
The surface area of a sphere is  . What is the diameter of the sphere?
. What is the diameter of the sphere?
The surface area of a sphere is 
The surface area of a sphere is given by 
So the equation to sovle becomes  or
or  so
so 
To answer the question we need to find the diameter:

The surface area of a sphere is given by
So the equation to sovle becomes 

To answer the question we need to find the diameter:
Compare your answer with the correct one above
A company wants to construct an advertising balloon spherical in shape. It can afford to buy 28,000 square meters of material to make the balloon. What is the largest possible diameter of this balloon (nearest whole meter)?
A company wants to construct an advertising balloon spherical in shape. It can afford to buy 28,000 square meters of material to make the balloon. What is the largest possible diameter of this balloon (nearest whole meter)?
This is equivalent to asking the diameter of a balloon with surface area 28,000 square meters.
The relationship between the surface area  and the radius
and the radius  is:
is:

To find the radius, substitute for the surface area, then solve:



To find the diameter  , double the radius—this is 94.
, double the radius—this is 94.
This is equivalent to asking the diameter of a balloon with surface area 28,000 square meters.
The relationship between the surface area 

To find the radius, substitute for the surface area, then solve:
To find the diameter 
Compare your answer with the correct one above
If the volume of a sphere is  , what is the sphere's diameter?
, what is the sphere's diameter?
If the volume of a sphere is 
Write the formula for the volume of a sphere:

Plug in the volume and find the radius by solving for  :
:

Start solving for  by multiplying both sides of the equation by
by multiplying both sides of the equation by  :
:


Now, divide each side of the equation by  :
:


Reduce the left side of the equation:

Finally, take the cubed root of both sides of the equation:
![\sqrt[3]{\frac{3}{2\pi}}=r](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/284622/gif.latex)
Keep in mind that you've solved for the radius, not the diameter. The diameter is double the radius, which is: ![2\sqrt[3]{\frac{3}{2\pi}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/284623/gif.latex) .
.
Write the formula for the volume of a sphere:
Plug in the volume and find the radius by solving for 
Start solving for 

Now, divide each side of the equation by 
Reduce the left side of the equation:
Finally, take the cubed root of both sides of the equation:
Keep in mind that you've solved for the radius, not the diameter. The diameter is double the radius, which is: ![2\sqrt[3]{\frac{3}{2\pi}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/284623/gif.latex)
Compare your answer with the correct one above