Trapezoids - Intermediate Geometry
Card 0 of 20
In the trapezoid below, find the degree measure of 
.
In the trapezoid below, find the degree measure of
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
degrees.
and the angle measuring 
degrees are adjacent angles that are supplementary.
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to
Compare your answer with the correct one above
In the trapezoid below, find the angle measurement of 
.
In the trapezoid below, find the angle measurement of
In a trapezoid, all the interior angles add up to 
degrees.
is 
degrees.
In a trapezoid, all the interior angles add up to
Compare your answer with the correct one above
In the trapezoid below, find the angle measurement of 
.
In the trapezoid below, find the angle measurement of
All the interior angles in a trapezoid add up to 
.
is 
degrees.
All the interior angles in a trapezoid add up to
Compare your answer with the correct one above
In the trapezoid below, find the angle measurement of 
.
In the trapezoid below, find the angle measurement of
All the interior angles in a trapezoid add up to 
.
is 
degrees.
All the interior angles in a trapezoid add up to
Compare your answer with the correct one above
In the trapezoid below, find the degree measurement of 
.
In the trapezoid below, find the degree measurement of
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
degrees.
and the angle measuring 
degrees are adjacent angles that are supplementary.
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to
Compare your answer with the correct one above
In the trapezoid below, find the degree measurement of 
.
In the trapezoid below, find the degree measurement of
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
degrees.
and the angle measuring 
degrees are adjacent angles that are supplementary.
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to
Compare your answer with the correct one above
In the trapezoid below, find the degree measurement of 
.
In the trapezoid below, find the degree measurement of
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
degrees.
and the angle measuring 
degrees are adjacent angles that are supplementary.
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to
Compare your answer with the correct one above
In the trapezoid below, find the degree measurement of 
.
In the trapezoid below, find the degree measurement of
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
degrees.
and the angle measuring 
degrees are adjacent angles that are supplementary.
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to
Compare your answer with the correct one above
In the trapezoid below, find the degree measurement of 
.
In the trapezoid below, find the degree measurement of
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
degrees.
and the angle measuring 
degrees are adjacent angles that are supplementary.
Therefore, we can write the following equation and solve for a.
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to
Therefore, we can write the following equation and solve for a.
Compare your answer with the correct one above
In the trapezoid below, find the degree measurement of 
.
In the trapezoid below, find the degree measurement of
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
degrees.
and the angle measuring 
degrees are adjacent angles that are supplementary.
Therefore, we can write the following equation and solve for z.
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to
Therefore, we can write the following equation and solve for z.
Compare your answer with the correct one above
In the trapezoid below, find the degree measurement of 
.
In the trapezoid below, find the degree measurement of
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
degrees.
and the angle measuring 
degrees are adjacent angles that are supplementary.
Therefore, we can write the following equations and solve for y.
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to
Therefore, we can write the following equations and solve for y.
Compare your answer with the correct one above
In the trapezoid below, find the degree measurement of 
.
In the trapezoid below, find the degree measurement of
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to 
degrees.
and the angle measuring 
degrees are adjacent angles that are supplementary.
Thus, we can write the following equation and solve for x.
In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to
Thus, we can write the following equation and solve for x.
Compare your answer with the correct one above
Given Trapezoid 
with bases 
and 
. The trapezoid has midsegment 
, where 
and 
are the midpoints of 
and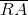 
, respectively.
True, false, or undetermined: Trapezoid 
Trapezoid 
.
Given Trapezoid
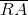
True, false, or undetermined: Trapezoid
The fact that the trapezoid is isosceles is actually irrelevant. Since 
and 
are the midpoints of legs 
and 
, it holds by definition that
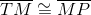
and
It follows that 
However, the bases of each trapezoid are noncongruent, by definition, so, in particular,
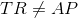
Assume that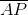 
is the longer base - this argument works symmetrically if the opposite is true. Let 
- equivalently, 
.
Since the bases are of unequal length, 
. The length of the midsegment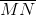 
is the arithmetic mean of the lengths of these two bases, so
Since 
, it follows that
,
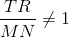and
.
This disproves similarity, since one condition is that corresponding sides must be in proportion.
The fact that the trapezoid is isosceles is actually irrelevant. Since
and
It follows that
However, the bases of each trapezoid are noncongruent, by definition, so, in particular,
Assume that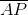
Since the bases are of unequal length,
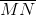
Since
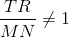
and
This disproves similarity, since one condition is that corresponding sides must be in proportion.
Compare your answer with the correct one above
Suppose the area of the trapezoid is 
, with a height of 
and a base of 
. What must be the length of the other base?
Suppose the area of the trapezoid is
Write the formula for finding the area of a trapezoid.
Substitute the givens and solve for either base.
Write the formula for finding the area of a trapezoid.
Substitute the givens and solve for either base.
Compare your answer with the correct one above
If the area of a trapezoid is 
, the height of the trapezoid is 
, and the base length is 
, what must be the length of the other base?
If the area of a trapezoid is
Write the formula for the area of a trapezoid.
Substitute all the given values and solve for the base.
Write the formula for the area of a trapezoid.
Substitute all the given values and solve for the base.
Compare your answer with the correct one above
An isosceles trapezoid has base measurements of 
and 
. The perimeter of the trapezoid is 
. Find the length for one of the two remaining sides.
An isosceles trapezoid has base measurements of
To solve this problem, first note that an isosceles trapezoid has two parallel bases that are nonequivalent in length. Additionally, an isosceles trapezoid must have two nonparallel sides that have equivalent lengths. Since this problem provides the length for both of the bases as well as the total perimeter, the missing sides can be found using the following formula: Perimeter= Base one 
Base two 
(leg), where the length of "leg" is one of the two equivalent nonparallel sides.
Thus, the solution is:
Check the solution by plugging in the answer:
To solve this problem, first note that an isosceles trapezoid has two parallel bases that are nonequivalent in length. Additionally, an isosceles trapezoid must have two nonparallel sides that have equivalent lengths. Since this problem provides the length for both of the bases as well as the total perimeter, the missing sides can be found using the following formula: Perimeter= Base one
Thus, the solution is:
Check the solution by plugging in the answer:
Compare your answer with the correct one above
An isosceles trapezoid has base measurements of 
and 
. Additionally, the isosceles trapezoid has a height of 
. Find the length for one of the two missing sides.
An isosceles trapezoid has base measurements of
In order to solve this problem, first note that an isosceles trapezoid has two parallel bases that are nonequivalent in length. Additionally, an isosceles trapezoid must have two nonparallel sides that have equivalent lengths.
This problem provides the lengths for each of the bases as well as the height of the isosceles trapezoid. In order to find the length for one of the two equivalent nonparallel legs of the trapezoid, first use the height of the trapezoid to form right triangles on the interior of the trapezoid that each have a base length of 
. See image below:
Note: the base length of 
can be found by subtracting the lengths of the two bases, then dividing that difference in half:
Now, apply the formula 
, where 
the length for one of the two equivalent nonparallel legs of the trapezoid.
Thus, the solution is:
In order to solve this problem, first note that an isosceles trapezoid has two parallel bases that are nonequivalent in length. Additionally, an isosceles trapezoid must have two nonparallel sides that have equivalent lengths.
This problem provides the lengths for each of the bases as well as the height of the isosceles trapezoid. In order to find the length for one of the two equivalent nonparallel legs of the trapezoid, first use the height of the trapezoid to form right triangles on the interior of the trapezoid that each have a base length of
Note: the base length of
Now, apply the formula
Thus, the solution is:
Compare your answer with the correct one above
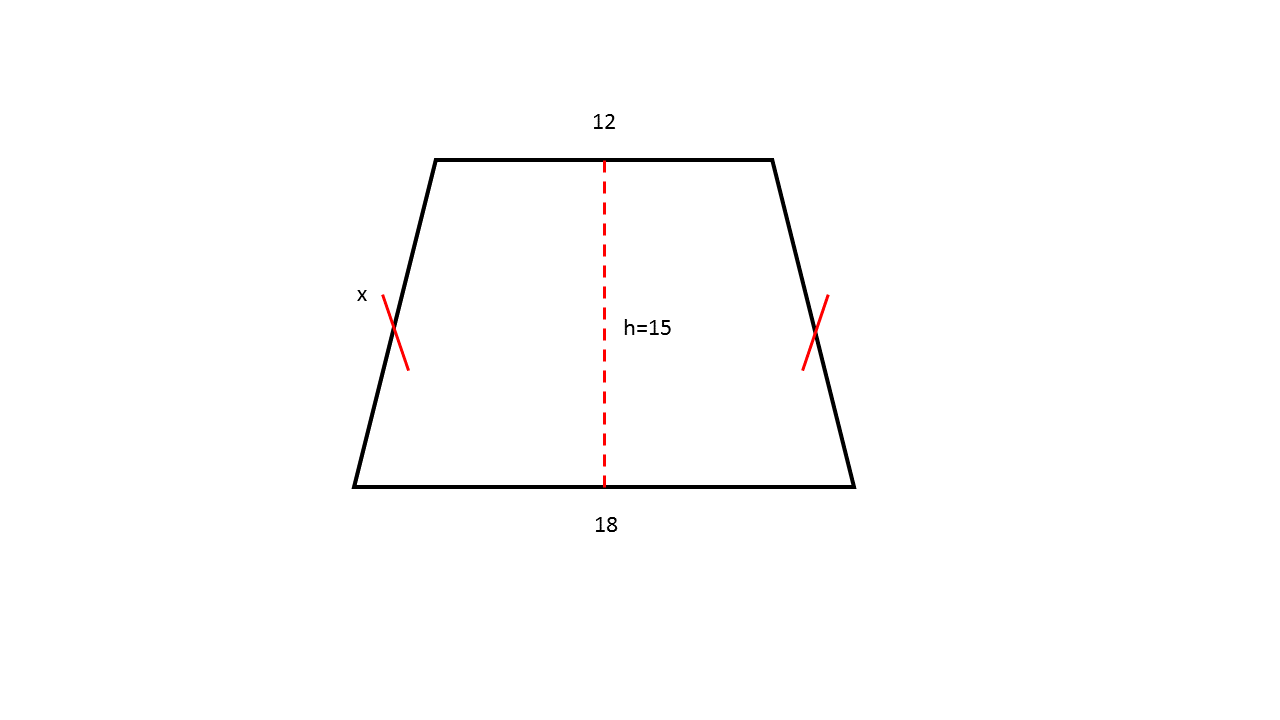
The isosceles trapezoid shown above has base measurements of 
and 
. Additionally, the trapezoid has a height of 
. Find the length of side 
.
The isosceles trapezoid shown above has base measurements of
In this problem the lengths for each of the bases and the height of the isosceles trapezoid is provided in the question prompt. In order to find the length for one of the two equivalent nonparallel legs of the trapezoid (side 
), first use the height of the trapezoid to form right triangles on the interior of the trapezoid that each have a base length of 
.
The base of the interior triangles is equal to 
because the difference between the two bases is equal to 
. And, this difference must be divided evenly in half because the isosceles trapezoid is symmetric--due to the two equivalent nonparallel sides and the two nonequivalent parallel bases.
Now, apply the pythagorean theorem: 
, where 
.
Thus, 
In this problem the lengths for each of the bases and the height of the isosceles trapezoid is provided in the question prompt. In order to find the length for one of the two equivalent nonparallel legs of the trapezoid (side
The base of the interior triangles is equal to
Now, apply the pythagorean theorem:
Thus,
Compare your answer with the correct one above
Using the trapezoid shown above, find the length of side 
.
Using the trapezoid shown above, find the length of side
In order to find the length of side 
, first note that the vertical side that has a length of 
and the base side with length 
must be perpendicular because they form a right angle. This means that the height of the trapezoid must equal 
. A right triangle can be formed on the interior of the trapezoid that has a height of 
and a base lenght of 
The base length can be derived by finding the difference between the two nonequivalent parallel bases.
Thus, the solution can be found by applying the formula: 
, where 
In order to find the length of side
Thus, the solution can be found by applying the formula:
Compare your answer with the correct one above
Using the isosceles trapezoid shown above, find the length for one of the two nonparallel equivalent sides.
Using the isosceles trapezoid shown above, find the length for one of the two nonparallel equivalent sides.
To solve this problem, first note that an isosceles trapezoid has two parallel bases that are nonequivalent in length. Additionally, an isosceles trapezoid must have two nonparallel sides that have equivalent lengths. Since this problem provides the length for both of the bases as well as the total perimeter, the missing sides can be found using the following formula: Perimeter= Base one Base two (leg), where the length of "leg" is one of the two equivalent nonparallel sides.
Thus, the solution is:
To solve this problem, first note that an isosceles trapezoid has two parallel bases that are nonequivalent in length. Additionally, an isosceles trapezoid must have two nonparallel sides that have equivalent lengths. Since this problem provides the length for both of the bases as well as the total perimeter, the missing sides can be found using the following formula: Perimeter= Base one
Thus, the solution is:
Compare your answer with the correct one above