Kites - Intermediate Geometry
Card 0 of 20
A kite has two different side lengths of 
and 
. Find the measurements for a similar kite.
A kite has two different side lengths of
A kite is a geometric shape that has two sets of equivalent adjacent sides. In order for two kites to be similar their sides must have the same ratios.
Since, the given kite has side lengths 
and 
, they have the ratio of 
.
Therefore, find the side lengths that have a ratio of 
.
The only answer choice with this ratio is: 
A kite is a geometric shape that has two sets of equivalent adjacent sides. In order for two kites to be similar their sides must have the same ratios.
Since, the given kite has side lengths
Therefore, find the side lengths that have a ratio of
The only answer choice with this ratio is:
Compare your answer with the correct one above
A kite has two different side lengths of 
and 
. Find the measurements for a similar kite.
A kite has two different side lengths of
A kite is a geometric shape that has two sets of equivalent adjacent sides. In order for two kites to be similar their sides must have the same ratios.
The given side lengths for the kite are 
and 
, which have the ratio of 
.
The only answer choice with the same relationship between side lengths is: 
and 
, which has the ratio of 
A kite is a geometric shape that has two sets of equivalent adjacent sides. In order for two kites to be similar their sides must have the same ratios.
The given side lengths for the kite are
The only answer choice with the same relationship between side lengths is:
Compare your answer with the correct one above
Suppose the ratio of a kite's side lengths is 
to 
. Find a similar kite.
Suppose the ratio of a kite's side lengths is
To find a similar kite, first take the ratios of the two sides and convert this to fractional form.
Rationalize the denominator.
The ratios of 
matches that of 
.
To find a similar kite, first take the ratios of the two sides and convert this to fractional form.
Rationalize the denominator.
The ratios of
Compare your answer with the correct one above
Suppose a kite has side lengths of 
and 
. What must the side lengths be for a similar kite?
Suppose a kite has side lengths of
Write the side lengths 4 and 5 as a ratio.
The only side lengths that match this ratio by a scale factor of 
is 
.
Therefore, the correct side lengths are 
.
Write the side lengths 4 and 5 as a ratio.
The only side lengths that match this ratio by a scale factor of
Therefore, the correct side lengths are
Compare your answer with the correct one above
The diagonals of a kite are 
inches and 
inches respectively. Two of the sides of the kite are each 
inches. Find the length of the other two sides.
The diagonals of a kite are
We would do best to begin with a picture.
One of our diagonals is bisected by the other, and thus each half is 12. The other important thing to recall is that the diagonals of a kite are perpendicular. Therefore we have four right triangles. We can then use the Pythagorean Theorem to calculate the upper portion of the vertical diagonal to be 5. That means that the bottom portion of our diagonal is 9.
Using the Pythagorean Theorem, we can calculate our remaining sides to be 15.
We would do best to begin with a picture.
One of our diagonals is bisected by the other, and thus each half is 12. The other important thing to recall is that the diagonals of a kite are perpendicular. Therefore we have four right triangles. We can then use the Pythagorean Theorem to calculate the upper portion of the vertical diagonal to be 5. That means that the bottom portion of our diagonal is 9.
Using the Pythagorean Theorem, we can calculate our remaining sides to be 15.
Compare your answer with the correct one above
A kite has a perimeter of 
inches. One pair of adjacent sides of the kite have a length of 
inches. What is the measurement for each of the other two sides of the kite?
A kite has a perimeter of
To find the missing side of this kite, work backwards using the formula:
, where 
and 
represent the length of one side from each of the two pairs of adjacent sides.
The solution is:
To find the missing side of this kite, work backwards using the formula:
The solution is:
Compare your answer with the correct one above
A kite has a perimeter of 
mm. One pair of adjacent sides of the kite have lengths of 
mm. What is the measurement for one of the other two sides of the kite?
A kite has a perimeter of
To find the missing side of this kite, work backwards using the formula:
, where 
and 
represent the length of one side from each of the two pairs of adjacent sides.
The solution is:
To find the missing side of this kite, work backwards using the formula:
The solution is:
Compare your answer with the correct one above
A kite has a perimeter of 
inches. One pair of adjacent sides of the kite have lengths of 
inches. What is the measurement for one of the other two sides of the kite?
A kite has a perimeter of
To find the missing side of this kite, work backwards using the formula:
, where and represent the length of one side from each of the two pairs of adjacent sides.
The solution is:
To find the missing side of this kite, work backwards using the formula:
The solution is:
Compare your answer with the correct one above
Using the kite shown above, find the length of side 
Using the kite shown above, find the length of side
To find the missing side of this kite, work backwards using the formula:
, where and represent the length of one side from each of the two pairs of adjacent sides.
The solution is:
To find the missing side of this kite, work backwards using the formula:
The solution is:
Compare your answer with the correct one above
Using the kite shown above, find the length of side 
. (Note, the perimeter of this kite is equal to 
feet).
Using the kite shown above, find the length of side
To find the missing side of this kite, work backwards using the formula:
, where and represent the length of one side from each of the two pairs of adjacent sides.
The solution is:
To find the missing side of this kite, work backwards using the formula:
The solution is:
Compare your answer with the correct one above
Ms. Dunn has a kite shaped backyard with a perimeter of 
yards. One pair of adjacent sides of the kite-shaped backyard each have lengths of 
yard. What is the measurement for one of the other two sides of the kite-shaped backyard?
Ms. Dunn has a kite shaped backyard with a perimeter of
To find the missing side of this kite, work backwards using the formula:
, where and represent the length of one side from each of the two pairs of adjacent sides.
The solution is:
To find the missing side of this kite, work backwards using the formula:
The solution is:
Compare your answer with the correct one above
A kite has a perimeter of 
mm. One pair of adjacent sides of the kite have lengths of 
mm. What is the measurement for one of the other two sides of the kite?
A kite has a perimeter of
To find the missing side of this kite, work backwards using the formula:
, where and represent the length of one side from each of the two pairs of adjacent sides.
The solution is:
To find the missing side of this kite, work backwards using the formula:
The solution is:
Compare your answer with the correct one above
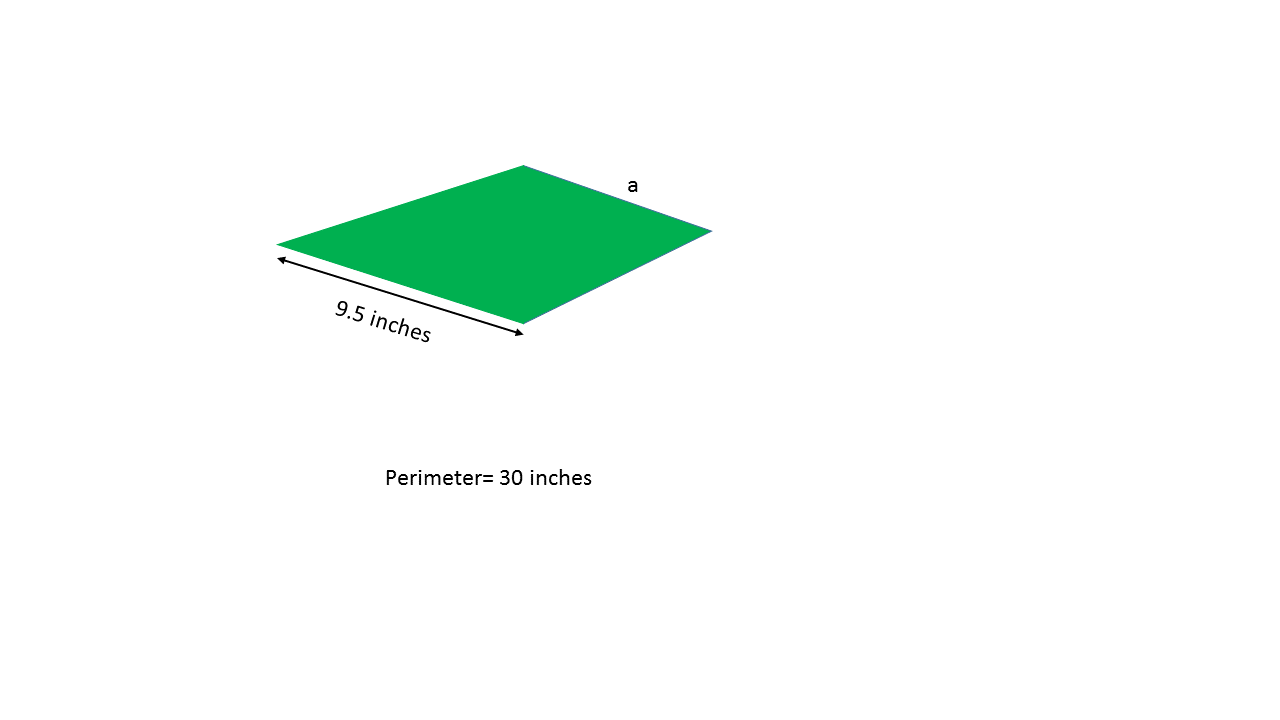
Using the above kite, find the length of side 
.
Using the above kite, find the length of side
To find the missing side of this kite, work backwards using the formula:
, where and represent the length of one side from each of the two pairs of adjacent sides.
The solution is:
To find the missing side of this kite, work backwards using the formula:
The solution is:
Compare your answer with the correct one above
The lengths of the non-adjacent sides of a kite have the ratio 
. If the longer sides have a length of 
cm, what is the length of each of the shorter two sides?
The lengths of the non-adjacent sides of a kite have the ratio
The sides have the ratio 
, thus the longer sides must be 
times greater than the smaller sides.
Since the longer sides are 
cm, the shorter sides must be:
The sides have the ratio
Since the longer sides are
Compare your answer with the correct one above
A kite has a perimeter of 
mm. One pair of adjacent sides of the kite have lengths of 
mm. What is the measurement for one of the other two sides of the kite?
A kite has a perimeter of
To find the missing side of this kite, work backwards using the formula:
, where and represent the length of one side from each of the two pairs of adjacent sides.
The solution is:
To find the missing side of this kite, work backwards using the formula:
The solution is:
Compare your answer with the correct one above
Find the longest side of the kite that is shown above.
Find the longest side of the kite that is shown above.
To find the missing side of this kite, work backwards using the formula:
, where and represent the length of one side from each of the two pairs of adjacent sides.
The solution is:
To find the missing side of this kite, work backwards using the formula:
The solution is:
Compare your answer with the correct one above
A kite has a perimeter of 
feet. One pair of adjacent sides of the kite have lengths of 
foot each. What is the measurement for one of the other two sides of the kite?
A kite has a perimeter of
To solve this problem use the formula , where and represent the length of one side from each of the two pairs of adjacent sides.
The solution is:
Make the first fraction into an improper fraction. Then find the reciprocal of the denominator and switch the operation sign:
To solve this problem use the formula
The solution is:
Make the first fraction into an improper fraction. Then find the reciprocal of the denominator and switch the operation sign:
Compare your answer with the correct one above
Given: Regular Pentagon 
with center 
. Construct segments 
and 
to form Quadrilateral 
.
True or false: Quadrilateral 
is a kite.
Given: Regular Pentagon
True or false: Quadrilateral
Below is regular Pentagon 
with center 
, a segment drawn from 
to each vertex - that is, each of its radii drawn.
A kite is a quadrilateral with two sets of congruent adjacent sides, with the common length of one pair differing from that of the other. A regular polygon has congruent sides, so 
; also, all radii of a regular polygon are congruent, so 
. It follows by definition that Quadrilateral 
is a kite.
Below is regular Pentagon
A kite is a quadrilateral with two sets of congruent adjacent sides, with the common length of one pair differing from that of the other. A regular polygon has congruent sides, so
Compare your answer with the correct one above
Using the kite shown above, find the length of side 
Using the kite shown above, find the length of side
A kite is a geometric shape that has two sets of equivalent adjacent sides.
Thus, the length of side 
.
Since, 
, 
must equal 
.
A kite is a geometric shape that has two sets of equivalent adjacent sides.
Thus, the length of side
Since,
Compare your answer with the correct one above
What is the length of side 
What is the length of side
A kite is a geometric shape that has two sets of equivalent adjacent sides. In this kite the two adjacent sides which are congruent are those at the top of the kite and then likewise, the two that are connected at the bottom of the kite.
Thus, 
must equal 
.
A kite is a geometric shape that has two sets of equivalent adjacent sides. In this kite the two adjacent sides which are congruent are those at the top of the kite and then likewise, the two that are connected at the bottom of the kite.
Thus,
Compare your answer with the correct one above