How to find the equation of a line - Intermediate Geometry
Card 0 of 20
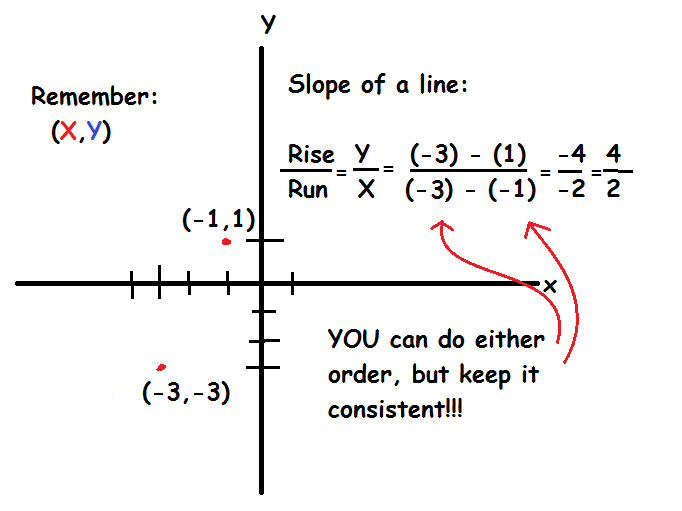
Given two points  and
and  , find the equation for the line connecting those two points in slope-intercept form.
, find the equation for the line connecting those two points in slope-intercept form.
Given two points 

If we have two points, we can find the slope of the line between them by using the definition of the slope:
 where the triangle is the greek letter 'Delta', and is used as a symbol for 'difference' or 'change in'
where the triangle is the greek letter 'Delta', and is used as a symbol for 'difference' or 'change in'
Now that we have our slope (  , simplified to
, simplified to  ), we can write the equation for slope-intercept form:
), we can write the equation for slope-intercept form:
 where
where  is the slope and
is the slope and  is the y-intercept
is the y-intercept

In order to find the y-intercept, we simply plug in one of the points on our line



So our equation looks like 
If we have two points, we can find the slope of the line between them by using the definition of the slope:

Now that we have our slope ( 




In order to find the y-intercept, we simply plug in one of the points on our line
So our equation looks like
Compare your answer with the correct one above
Which of the following is an equation for a line with a slope of  and a y-intercept of
and a y-intercept of  ?
?
Which of the following is an equation for a line with a slope of 

Because we have the desired slope and the y-intercept, we can easily write this as an equation in slope-intercept form (y=mx+b).
This gives us  . Because this does not match either of the answers in this form (y=mx+b), we must solve the equation for x. Adding 5 to each side gives us
. Because this does not match either of the answers in this form (y=mx+b), we must solve the equation for x. Adding 5 to each side gives us  . We can then multiple both sides by 3 and divide both sides by 4, giving us
. We can then multiple both sides by 3 and divide both sides by 4, giving us  .
.
Because we have the desired slope and the y-intercept, we can easily write this as an equation in slope-intercept form (y=mx+b).
This gives us 


Compare your answer with the correct one above
If the  -intercept of a line is
-intercept of a line is  , and the
, and the  -intercept is
-intercept is  , what is the equation of this line?
, what is the equation of this line?
If the 



If the y-intercept of a line is  , then the
, then the  -value is
-value is  when
when  is zero. Write the point:
is zero. Write the point:

If the  -intercept of a line is
-intercept of a line is  , then the
, then the  -value is
-value is  when
when  is zero. Write the point:
is zero. Write the point:

Use the following formula for slope and the two points to determine the slope:

Use the slope intercept form and one of the points, suppose  , to find the equation of the line by substituting in the values of the point and solving for
, to find the equation of the line by substituting in the values of the point and solving for  , the
, the  -intercept.
-intercept.



Therefore, the equation of this line is  .
.
If the y-intercept of a line is 



If the 




Use the following formula for slope and the two points to determine the slope:
Use the slope intercept form and one of the points, suppose 


Therefore, the equation of this line is 
Compare your answer with the correct one above
A line goes through the following points  and
and  .
.
Find the equation of the line.
A line goes through the following points 

Find the equation of the line.
First, find the slope of the line using the slope formula:
 .
.
Next we plug one of the points, and the slope, into the point-intercept line forumula:
 where m is our slope.
where m is our slope.
Then  and when we plug in point (2,3) the formula reads
and when we plug in point (2,3) the formula reads  then solve for b.
then solve for b.
 .
.
To find the equation of the line, we plug in our m and b into the slope-intercept equation.
So,  or simplified,
or simplified,  .
.
First, find the slope of the line using the slope formula:

Next we plug one of the points, and the slope, into the point-intercept line forumula:

Then 


To find the equation of the line, we plug in our m and b into the slope-intercept equation.
So, 

Compare your answer with the correct one above
What is the equation of a line that has a slope of  and a
and a  -intercept of
-intercept of  ?
?
What is the equation of a line that has a slope of 


The slope intercept form can be written as:

where  is the slope and
is the slope and  is the y-intercept. Plug in the values of the slope and
is the y-intercept. Plug in the values of the slope and  -intercept into the equation.
-intercept into the equation.
The correct answer is: 
The slope intercept form can be written as:
where 


The correct answer is:
Compare your answer with the correct one above
What is the equation of a line with a slope of  and an
and an  -intercept of
-intercept of  ?
?
What is the equation of a line with a slope of 


The  -intercept is the value of
-intercept is the value of  when the
when the  value is equal to zero. The actual point located on the graph for an
value is equal to zero. The actual point located on the graph for an  -intercept of
-intercept of  is
is  . The slope,
. The slope,  , is 2.
, is 2.
Write the slope-intercept equation and substitute the point and slope to solve for the  -intercept:
-intercept:



Plug the slope and  -intercept back in the slope-intercept formula:
-intercept back in the slope-intercept formula:

The 






Write the slope-intercept equation and substitute the point and slope to solve for the 
Plug the slope and 
Compare your answer with the correct one above
Write the equation for the line passing through the points  and
and 
Write the equation for the line passing through the points 
To determine the equation, first find the slope:

We want this equation in slope-intercept form,  . We know
. We know  and
and  because we have two coordinate pairs to choose from representing an
because we have two coordinate pairs to choose from representing an  and a
and a  . We know
. We know  because that represents the slope. We just need to solve for
because that represents the slope. We just need to solve for  , and then we can write the equation.
, and then we can write the equation.
We can choose either point and get the correct answer. Let's choose  :
:
 multiply "
multiply " "
"
 add
add  to both sides
to both sides

This means that the  form is
form is 
To determine the equation, first find the slope:
We want this equation in slope-intercept form, 






We can choose either point and get the correct answer. Let's choose 




This means that the 
Compare your answer with the correct one above
Write the equation for a line that passes through the points  and
and  .
.
Write the equation for a line that passes through the points 

To determine the equation, first find the slope:

We want this equation in slope-intercept form,  . We know
. We know  and
and  because we have two coordinate pairs to choose from representing an
because we have two coordinate pairs to choose from representing an  and a
and a  . We know
. We know  because that represents the slope. We just need to solve for
because that represents the slope. We just need to solve for  , and then we can write the equation.
, and then we can write the equation.
We can choose either point and get the correct answer. Let's choose  :
:
 multiply "
multiply " "
"
 subtract
subtract  from both sides
from both sides

This means that the  form is
form is 
To determine the equation, first find the slope:
We want this equation in slope-intercept form, 






We can choose either point and get the correct answer. Let's choose 




This means that the 
Compare your answer with the correct one above
Find the equation for a line passing through the points  and
and  .
.
Find the equation for a line passing through the points 

To determine the equation, first find the slope:

We want this equation in slope-intercept form,  . We know
. We know  and
and  because we have two coordinate pairs to choose from representing an
because we have two coordinate pairs to choose from representing an  and a
and a  . We know
. We know  because that represents the slope. We just need to solve for
because that represents the slope. We just need to solve for  , and then we can write the equation.
, and then we can write the equation.
We can choose either point and get the correct answer. Let's choose  :
:
 multiply "
multiply " "
"
 subtract
subtract  from both sides
from both sides

This means that the  form is
form is 
To determine the equation, first find the slope:
We want this equation in slope-intercept form, 






We can choose either point and get the correct answer. Let's choose 




This means that the 
Compare your answer with the correct one above
Find the equation for the line passing through the points  and
and  .
.
Find the equation for the line passing through the points 

To determine the equation, first find the slope:

We want this equation in slope-intercept form,  . We know
. We know  and
and  because we have two coordinate pairs to choose from representing an
because we have two coordinate pairs to choose from representing an  and a
and a  . We know
. We know  because that represents the slope. We just need to solve for
because that represents the slope. We just need to solve for  , and then we can write the equation.
, and then we can write the equation.
We can choose either point and get the correct answer. Let's choose  :
:
 multiply "
multiply " "
"
 subtract
subtract  from both sides
from both sides

This means that the  form is
form is 
To determine the equation, first find the slope:
We want this equation in slope-intercept form, 






We can choose either point and get the correct answer. Let's choose 




This means that the 
Compare your answer with the correct one above
Write the equation for the line passing through the points  and
and  .
.
Write the equation for the line passing through the points 

First, find the slope of the line:

Now we want to find the y-intercept. We can figure this out by plugging in the slope for "m" and one of the points in for x and y in the formula  :
:



The equation is 
First, find the slope of the line:
Now we want to find the y-intercept. We can figure this out by plugging in the slope for "m" and one of the points in for x and y in the formula 
The equation is
Compare your answer with the correct one above
Find the equation for the line passing through the points  and
and  .
.
Find the equation for the line passing through the points 

First, determine the slope of the line using the slope formula:

The equation will be in the form  where m is the slope that we just determined, and b is the y-intercept. To determine that, we can plug in the slope for m and the coordinates of one of the original points for x and y:
where m is the slope that we just determined, and b is the y-intercept. To determine that, we can plug in the slope for m and the coordinates of one of the original points for x and y:

 to subtract, it will be easier to convert 3 to a fraction,
to subtract, it will be easier to convert 3 to a fraction, 


The equation is 
First, determine the slope of the line using the slope formula:
The equation will be in the form 

The equation is
Compare your answer with the correct one above
Find the equation of a line passing through the points  and
and  .
.
Find the equation of a line passing through the points 

To find the equation of a line passing through these points we must find a line with that same slope. Start by finding the slope between the two points and then use the point slope equation to find the equation of the line.
slope:

Now use the point slope equation:

*make sure you use the SAME coordinate pair when substituting x and y into the point slope equation.
To find the equation of a line passing through these points we must find a line with that same slope. Start by finding the slope between the two points and then use the point slope equation to find the equation of the line.
slope:
Now use the point slope equation:
*make sure you use the SAME coordinate pair when substituting x and y into the point slope equation.
Compare your answer with the correct one above
Find the equation of a line that passes through the following points:
 and
and 
Find the equation of a line that passes through the following points:

Recall that the the following is the slope-intercept form of a line:

In this equation, the variables are represented by the following:


Find the slope of the line by using the following formula:

In this equation, the x- and y-variables correspond to the coordinates of the given points.



Next, find the y-intercept of the line by substituting one of the points into the semi-completed formula.

Substituting in the point  yields the following:
yields the following:

Rearrange and solve for  .
.

Subtract 20 from both sides of the equation.


Substitute this value of the y-intercept into our semi-complete equation to get the answer:

Recall that the the following is the slope-intercept form of a line:
In this equation, the variables are represented by the following:
Find the slope of the line by using the following formula:
In this equation, the x- and y-variables correspond to the coordinates of the given points.
Next, find the y-intercept of the line by substituting one of the points into the semi-completed formula.
Substituting in the point 
Rearrange and solve for 
Subtract 20 from both sides of the equation.
Substitute this value of the y-intercept into our semi-complete equation to get the answer:
Compare your answer with the correct one above
Find the equation of a line that goes through the points  and
and  .
.
Find the equation of a line that goes through the points 

Recall that the slope-intercept form of a line:
 ,
,
where  and
and  .
.
First, find the slope of the line by using the following formula:


Next, find the y-intercept of the line by plugging in  of the points into the semi-completed formula.
of the points into the semi-completed formula.

Plugging in  yields the following:
yields the following:

Solve for  .
.


The equation of the line is then  .
.
Recall that the slope-intercept form of a line:

where 

First, find the slope of the line by using the following formula:
Next, find the y-intercept of the line by plugging in 
Plugging in 
Solve for 
The equation of the line is then 
Compare your answer with the correct one above
Find the equation of a line that goes through the points  and
and  .
.
Find the equation of a line that goes through the points 

Recall that the slope-intercept form of a line:
 ,
,
where  and
and  .
.
First, find the slope of the line by using the following formula:


Next, find the y-intercept of the line by plugging in  of the points into the semi-completed formula.
of the points into the semi-completed formula.

Plugging in  yields the following:
yields the following:

Solve for  .
.


The equation of the line is then  .
.
Recall that the slope-intercept form of a line:

where 

First, find the slope of the line by using the following formula:
Next, find the y-intercept of the line by plugging in 
Plugging in 
Solve for 
The equation of the line is then 
Compare your answer with the correct one above
Find the equation of a line that goes through the points  and
and  .
.
Find the equation of a line that goes through the points 

Recall that the slope-intercept form of a line:
 ,
,
where  and
and  .
.
First, find the slope of the line by using the following formula:


Next, find the y-intercept of the line by plugging in  of the points into the semi-completed formula.
of the points into the semi-completed formula.

Plugging in  yields the following:
yields the following:

Solve for  .
.


The equation of the line is then  .
.
Recall that the slope-intercept form of a line:

where 

First, find the slope of the line by using the following formula:
Next, find the y-intercept of the line by plugging in 
Plugging in 
Solve for 
The equation of the line is then 
Compare your answer with the correct one above
Find the equation of a line that goes through the points  and
and  .
.
Find the equation of a line that goes through the points 

Recall that the slope-intercept form of a line:
 ,
,
where  and
and  .
.
First, find the slope of the line by using the following formula:


Next, find the y-intercept of the line by plugging in  of the points into the semi-completed formula.
of the points into the semi-completed formula.

Plugging in  yields the following:
yields the following:

Solve for  .
.


The equation of the line is then  .
.
Recall that the slope-intercept form of a line:

where 

First, find the slope of the line by using the following formula:
Next, find the y-intercept of the line by plugging in 
Plugging in 
Solve for 
The equation of the line is then 
Compare your answer with the correct one above
Find the equation of the line that goes through the points  and
and  .
.
Find the equation of the line that goes through the points 

Recall that the slope-intercept form of a line:
 ,
,
where  and
and  .
.
First, find the slope of the line by using the following formula:


The y-intercept is  since that is given as one of the points on the line.
since that is given as one of the points on the line.
The line must have the equation  .
.
Recall that the slope-intercept form of a line:

where 

First, find the slope of the line by using the following formula:
The y-intercept is 
The line must have the equation 
Compare your answer with the correct one above
Find the equation of the line that goes through the points  and
and  .
.
Find the equation of the line that goes through the points 

Recall that the slope-intercept form of a line:
 ,
,
where  and
and  .
.
First, find the slope of the line by using the following formula:


Next, find the y-intercept of the line by plugging in  of the points into the semi-completed formula.
of the points into the semi-completed formula.

Plugging in  yields the following:
yields the following:

Solve for  .
.


The equation of the line is then  .
.
Recall that the slope-intercept form of a line:

where 

First, find the slope of the line by using the following formula:
Next, find the y-intercept of the line by plugging in 
Plugging in 
Solve for 
The equation of the line is then 
Compare your answer with the correct one above