How to find the area of a sector - Intermediate Geometry

Card 0 of 20

Question

The radius of the circle above is and $\angle A=45^{\circ}$ . What is the area of the shaded section of the circle?

Answer

Area of Circle = πr2 = π42 = 16π

Total degrees in a circle = 360

Therefore 45 degree slice = 45/360 fraction of circle = 1/8

Shaded Area = 1/8 * Total Area = 1/8 * 16π = 2π

Compare your answer with the correct one above

Question

Find the approximate area of the shaded portion of the figure.

Answer

The answer is approximately $6200\ cm^{2}$ .

First, you would need to find the diameter of the circle. Use the Pythagorean Theorem to get

$50^{2}+120^{2}=130^{2}$

or

$78^{2}+104^{2}=130^{2}$

Since the diameter is 130, we divide by 2 to get 65 cm for our radius. Then the area of the circle is

$\pi r^{2} = \pi \cdot 65^{2} \approx 13,273 \ cm^{2}$

Next we would find the area of each triangle:

$\frac{1}{2} (50)(120) = 3000cm^{2}$

and

$\frac{1}{2} (78)(104) = 4056cm^{2}$

Then we would subtract these from our answer above to get:

$13273-3000 - 4056 \approx 6200\ cm^{2}$ .

Compare your answer with the correct one above

Question

Give the area of a sector of a circle if its central angle is $20^{\circ }$ and the length of its arc is 10 inches. Write the answer in terms of $\pi$ , if applicable.

Answer

The arc of the $20^{\circ }$ sector measures 10 inches, so the circumference of the entire circle is

$C=10 \cdot\frac{360}{20}=180$

The radius is therefore

$r=\frac{C}{2\pi }=\frac{180}{2\pi }=\frac{90}{\pi }$

The area of a $20^{\circ }$ sector of this circle measures:

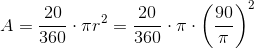
$A = \frac{20}{360}\cdot\pi r^{2}= \frac{20}{360}\cdot\pi \cdot \left (\frac{90}{\pi } \right )^{2}$

$=\frac{20\cdot 90\cdot 90\cdot \pi }{360\cdot \pi \cdot \pi }=\frac{450}{\pi }$

Compare your answer with the correct one above

Question

A circle has a diameter of meters. A certain sector of the circle has a central angle of $\small 20^\circ$ . Find the area of the sector.

Answer

The formula for the area of a sector is.

$\small S=\frac{m}{360}\pi r^2$ where $\small r$ is the radius and $\small m$ is the measure of the central angle of the sector.

We are given that the diameter of the circle is 60. Therefore its radius is simply half as long, or 30.

Substituting into our equation gives

$\small \small S=\frac{20}{360}\pi(30^2)=\frac{1}{18}\pi(900)=50\pi$

Therefore our area is $\small 50\pi,m^2$

Compare your answer with the correct one above

Question

If the sector in the provided illustration has an angle of $37.5^{\circ}$ and the circle has a radius of , what is the area of the sector? Round to the nearest tenth.

Answer

To solve for the area of the sector, it helps to solve for the area of the complete circle and multiple that value by the sector angle over the full $360^{\circ}$ of a complete circle:

$\Sector;Area=\pi\cdot(4.2;cm)^2\cdot\frac{37.5^{\circ}}{360^{\circ}}\Sector;Area=55.42;cm^2\cdot\frac{37.5^{\circ}}{360^{\circ}}\approx5.8;cm^2$

Compare your answer with the correct one above

Question

Find the area of a sector with a central angle of degrees and a radius of .

Answer

The circle in question could be depicted as shown in the figure.

Recall the formula for finding the area of a sector of a circle:

$\text{Area of Sector}=\frac{\text{Central Angle}}{360}\times\pi\times r^2$

Since the central angle and the radius are given in the question, plug them in to find the area of the sector.

$\text{Area of Sector}=\frac{124}{360}\times\pi\times 12^2$

Solve and round to two decimal places.

$\text{Area of Sector}=155.82$

Compare your answer with the correct one above

Question

Find the area of a sector that has a central angle of degrees and a radius of .

Answer

The circle in question could be depicted as shown in the figure.

Recall the formula for finding the area of a sector of a circle:

$\text{Area of Sector}=\frac{\text{Central Angle}}{360}\times\pi\times r^2$

Since the central angle and the radius are given in the question, plug them in to find the area of the sector.

$\text{Area of Sector}=\frac{129}{360}\times\pi\times 13^2$

Solve and round to two decimal places.

$\text{Area of Sector}=190.25$

Compare your answer with the correct one above

Question

Find the area of a sector that has a central angle of degrees and a radius of .

Answer

The circle in question could be depicted as shown in the figure.

Recall the formula for finding the area of a sector of a circle:

$\text{Area of Sector}=\frac{\text{Central Angle}}{360}\times\pi\times r^2$

Since the central angle and the radius are given in the question, plug them in to find the area of the sector.

$\text{Area of Sector}=\frac{130}{360}\times\pi\times 19^2$

Solve and round to two decimal places.

$\text{Area of Sector}=409.54$

Compare your answer with the correct one above

Question

Find the area of a sector that has a central angle of degrees and a radius of .

Answer

The circle in question could be depicted as shown in the figure.

Recall the formula for finding the area of a sector of a circle:

$\text{Area of Sector}=\frac{\text{Central Angle}}{360}\times\pi\times r^2$

Since the central angle and the radius are given in the question, plug them in to find the area of the sector.

$\text{Area of Sector}=\frac{135}{360}\times\pi\times 21^2$

Solve and round to two decimal places.

$\text{Area of Sector}=519.54$

Compare your answer with the correct one above

Question

Find the area of a sector that has a central angle of degrees and a radius of .

Answer

The circle in question could be depicted as shown in the figure.

Recall the formula for finding the area of a sector of a circle:

$\text{Area of Sector}=\frac{\text{Central Angle}}{360}\times\pi\times r^2$

Since the central angle and the radius are given in the question, plug them in to find the area of the sector.

$\text{Area of Sector}=\frac{115}{360}\times\pi\times 8^2$

Solve and round to two decimal places.

$\text{Area of Sector}=64.23$

Compare your answer with the correct one above

Question

Find the area of a sector that has a central angle of degrees and a radius of .

Answer

The circle in question could be depicted as shown in the figure.

Recall the formula for finding the area of a sector of a circle:

$\text{Area of Sector}=\frac{\text{Central Angle}}{360}\times\pi\times r^2$

Since the central angle and the radius are given in the question, plug them in to find the area of the sector.

$\text{Area of Sector}=\frac{118}{360}\times\pi\times 10^2$

Solve and round to two decimal places.

$\text{Area of Sector}=102.97$

Compare your answer with the correct one above

Question

Find the area of a sector that has a central angle of degrees and a radius of .

Answer

The circle in question could be depicted as shown in the figure.

Recall the formula for finding the area of a sector of a circle:

$\text{Area of Sector}=\frac{\text{Central Angle}}{360}\times\pi\times r^2$

Since the central angle and the radius are given in the question, plug them in to find the area of the sector.

$\text{Area of Sector}=\frac{34}{360}\times\pi\times 5^2$

Solve and round to two decimal places.

$\text{Area of Sector}=7.42$

Compare your answer with the correct one above

Question

Find the area of a sector that has a central angle of degrees and a radius of .

Answer

The circle in question could be depicted as shown in the figure.

Recall the formula for finding the area of a sector of a circle:

$\text{Area of Sector}=\frac{\text{Central Angle}}{360}\times\pi\times r^2$

Since the central angle and the radius are given in the question, plug them in to find the area of the sector.

$\text{Area of Sector}=\frac{26}{360}\times\pi\times 16^2$

Solve and round to two decimal places.

$\text{Area of Sector}=58.08$

Compare your answer with the correct one above

Question

Find the area of a sector that has a central angle of degrees and a radius of .

Answer

The circle in question could be depicted as shown in the figure.

Recall the formula for finding the area of a sector of a circle:

$\text{Area of Sector}=\frac{\text{Central Angle}}{360}\times\pi\times r^2$

Since the central angle and the radius are given in the question, plug them in to find the area of the sector.

$\text{Area of Sector}=\frac{35}{360}\times\pi\times 15^2$

Solve and round to two decimal places.

$\text{Area of Sector}=68.72$

Compare your answer with the correct one above

Question

Find the area of a sector that has a central angle of degrees and a radius of .

Answer

The circle in question could be depicted as shown in the figure.

Recall the formula for finding the area of a sector of a circle:

$\text{Area of Sector}=\frac{\text{Central Angle}}{360}\times\pi\times r^2$

Since the central angle and the radius are given in the question, plug them in to find the area of the sector.

$\text{Area of Sector}=\frac{15}{360}\times\pi\times 29^2$

Solve and round to two decimal places.

$\text{Area of Sector}=110.09$

Compare your answer with the correct one above

Question

Find the area of a sector that has a central angle of degrees and a radius of .

Answer

The circle in question could be depicted as shown in the figure.

Recall the formula for finding the area of a sector of a circle:

$\text{Area of Sector}=\frac{\text{Central Angle}}{360}\times\pi\times r^2$

Since the central angle and the radius are given in the question, plug them in to find the area of the sector.

$\text{Area of Sector}=\frac{40}{360}\times\pi\times 3^2$

Solve and round to two decimal places.

$\text{Area of Sector}=3.14$

Compare your answer with the correct one above

Question

Find the area of a sector that has a central angle of degrees and a radius of .

Answer

The circle in question could be depicted as shown in the figure.

Recall the formula for finding the area of a sector of a circle:

$\text{Area of Sector}=\frac{\text{Central Angle}}{360}\times\pi\times r^2$

Since the central angle and the radius are given in the question, plug them in to find the area of the sector.

$\text{Area of Sector}=\frac{33}{360}\times\pi\times 6^2$

Solve and round to two decimal places.

$\text{Area of Sector}=10.37$

Compare your answer with the correct one above

Question

Find the area of the sector that has a central angle of degrees and a radius of .

Answer

The circle in question can be drawn as shown by the figure below:

Since the area of a sector is just a fractional part of the area of a circle, we can write the following equation to find the area of a sector:

$\text{Area of Sector}=\frac{\text{Central angle}}{360}\pi r^2$ , where is the radius of the circle.

Plug in the given central angle and radius to find the area of the sector.

$\text{Area of Sector}=\frac{160}{360}\pi(12)^2=201.06$

Make sure to round to two places after the decimal.

Compare your answer with the correct one above

Question

Find the area of a sector that has a central angle of degrees and a radius of .

Answer

The circle in question can be drawn as shown by the figure below:

Since the area of a sector is just a fractional part of the area of a circle, we can write the following equation to find the area of a sector:

$\text{Area of Sector}=\frac{\text{Central angle}}{360}\pi r^2$ , where is the radius of the circle.

Plug in the given central angle and radius to find the area of the sector.

$\text{Area of Sector}=\frac{170}{360}\pi(3)^2=13.35$

Make sure to round to two places after the decimal.

Compare your answer with the correct one above

Question

Find the area of a sector that has a central angle of degrees and a radius of .

Answer

The circle in question can be drawn as shown by the figure below:

Since the area of a sector is just a fractional part of the area of a circle, we can write the following equation to find the area of a sector:

$\text{Area of Sector}=\frac{\text{Central angle}}{360}\pi r^2$ , where is the radius of the circle.

Plug in the given central angle and radius to find the area of the sector.

$\text{Area of Sector}=\frac{260}{360}\pi(5)^2=56.72$

Make sure to round to two places after the decimal.

Compare your answer with the correct one above

Tap the card to reveal the answer