How to find surface area - HSPT Math
Card 0 of 20
A spherical orange fits snugly inside a small cubical box such that each of the six walls of the box just barely touches the surface of the orange. If the volume of the box is 64 cubic inches, what is the surface area of the orange in square inches?
A spherical orange fits snugly inside a small cubical box such that each of the six walls of the box just barely touches the surface of the orange. If the volume of the box is 64 cubic inches, what is the surface area of the orange in square inches?
The volume of a cube is found by V = s3. Since V = 64, s = 4. The side of the cube is the same as the diameter of the sphere. Since d = 4, r = 2. The surface area of a sphere is found by SA = 4π(r2) = 4π(22) = 16π.
The volume of a cube is found by V = s3. Since V = 64, s = 4. The side of the cube is the same as the diameter of the sphere. Since d = 4, r = 2. The surface area of a sphere is found by SA = 4π(r2) = 4π(22) = 16π.
Compare your answer with the correct one above
An upright cylinder with a height of 30 and a radius of 5 is in a big tub being filled with oil. If only the top 10% of the cylinder is visible, what is the surface area of the submerged cylinder?
An upright cylinder with a height of 30 and a radius of 5 is in a big tub being filled with oil. If only the top 10% of the cylinder is visible, what is the surface area of the submerged cylinder?
The height of the submerged part of the cylinder is 27cm. 2πrh + πr2 is equal to 270π + 25π = 295π
The height of the submerged part of the cylinder is 27cm. 2πrh + πr2 is equal to 270π + 25π = 295π
Compare your answer with the correct one above
The diameter of the lid of a right cylindrical soup can is 5 in. If the can is 12 inches tall and the label costs $0.00125 per square inch to print, what is the cost to produce a label for a can? (Round to the nearest cent.)
The diameter of the lid of a right cylindrical soup can is 5 in. If the can is 12 inches tall and the label costs $0.00125 per square inch to print, what is the cost to produce a label for a can? (Round to the nearest cent.)
The general mechanics of this problem are simple. The lateral area of a right cylinder (excluding its top and bottom) is equal to the circumference of the top times the height of the cylinder. Therefore, the area of this can's surface is: 5π * 12 or 60π. If the cost per square inch is $0.00125, a single label will cost 0.00125 * 60π or $0.075π or approximately $0.24.
The general mechanics of this problem are simple. The lateral area of a right cylinder (excluding its top and bottom) is equal to the circumference of the top times the height of the cylinder. Therefore, the area of this can's surface is: 5π * 12 or 60π. If the cost per square inch is $0.00125, a single label will cost 0.00125 * 60π or $0.075π or approximately $0.24.
Compare your answer with the correct one above
Aluminum is sold to a soup manufacturer at a rate of $0.0015 per square inch. The cans are made so that the ends perfectly fit on the cylindrical body of the can. It costs $0.00125 to attach the ends to the can. The outer label (not covering the top / bottom) costs $0.0001 per in2 to print and stick to the can. The label must be 2 inches longer than circumference of the can. Ignoring any potential waste, what is the manufacturing cost (to the nearest cent) for a can with a radius of 5 inches and a height of 12 inches?
Aluminum is sold to a soup manufacturer at a rate of $0.0015 per square inch. The cans are made so that the ends perfectly fit on the cylindrical body of the can. It costs $0.00125 to attach the ends to the can. The outer label (not covering the top / bottom) costs $0.0001 per in2 to print and stick to the can. The label must be 2 inches longer than circumference of the can. Ignoring any potential waste, what is the manufacturing cost (to the nearest cent) for a can with a radius of 5 inches and a height of 12 inches?
We have the following categories to consider:
= ( + ) * 0.0015
= 2 * 0.00125 = $0.0025
The area of ends of the can are each equal to π*52 or 25π. For two ends, that is 50π.
The lateral area of the can is equal to the circumference of the top times the height, or 2 * π * r * h = 2 * 5 * 12 * π = 120π.
Therefore, the total surface area of the aluminum can is 120π + 50π = 170π. The cost is 170π * 0.0015 = 0.255π, or approximately $0.80.
The area of the label is NOT the same as the lateral area of the can. (Recall that it must be 2 inches longer than the circumference of the can.) Therefore, the area of the label is (2 + 2 * π * 5) * 12 = (2 + 10π) * 12 = 24 + 120π. Multiply this by 0.0001 to get 0.0024 + 0.012π = (approximately) $0.04.
Therefore, the total cost is approximately 0.80 + 0.04 + 0.0025 = $0.8425, or $0.84.
We have the following categories to consider:
The area of ends of the can are each equal to π*52 or 25π. For two ends, that is 50π.
The lateral area of the can is equal to the circumference of the top times the height, or 2 * π * r * h = 2 * 5 * 12 * π = 120π.
Therefore, the total surface area of the aluminum can is 120π + 50π = 170π. The cost is 170π * 0.0015 = 0.255π, or approximately $0.80.
The area of the label is NOT the same as the lateral area of the can. (Recall that it must be 2 inches longer than the circumference of the can.) Therefore, the area of the label is (2 + 2 * π * 5) * 12 = (2 + 10π) * 12 = 24 + 120π. Multiply this by 0.0001 to get 0.0024 + 0.012π = (approximately) $0.04.
Therefore, the total cost is approximately 0.80 + 0.04 + 0.0025 = $0.8425, or $0.84.
Compare your answer with the correct one above
A room has dimensions of 18ft by 15ft by 9ft. The last dimension is the height of the room. It has one door that is 3ft by 7ft and two windows, each 2ft by 5ft. There is no trim to the floor, wall, doors, or windows. What is the total exposed wall space?
A room has dimensions of 18ft by 15ft by 9ft. The last dimension is the height of the room. It has one door that is 3ft by 7ft and two windows, each 2ft by 5ft. There is no trim to the floor, wall, doors, or windows. What is the total exposed wall space?
If broken down into parts, this is an easy problem. It is first necessary to isolate the dimensions of the walls. If the room is 9 ft high, we know 18 x 15 designates the area of the floor and ceiling. Based on this, we know that the room has the following dimensions for the walls: 18 x 9 and 15 x 9. Since there are two of each, we can calculate the total area of walls - ignoring doors and windows - by doubling the sum of these two areas:
2 * (18 * 9 + 15 * 9) = 2 * (162 + 135) = 2 * 297 = 594 ft2
Now, we merely need to calculate the area "taken out" of the walls:
For the door: 3 * 7 = 21 ft2
For the windows: 2 * (2 * 5) = 20 ft2
The total wall space is therefore: 594 – 21 – 20 = 553 ft2
If broken down into parts, this is an easy problem. It is first necessary to isolate the dimensions of the walls. If the room is 9 ft high, we know 18 x 15 designates the area of the floor and ceiling. Based on this, we know that the room has the following dimensions for the walls: 18 x 9 and 15 x 9. Since there are two of each, we can calculate the total area of walls - ignoring doors and windows - by doubling the sum of these two areas:
2 * (18 * 9 + 15 * 9) = 2 * (162 + 135) = 2 * 297 = 594 ft2
Now, we merely need to calculate the area "taken out" of the walls:
For the door: 3 * 7 = 21 ft2
For the windows: 2 * (2 * 5) = 20 ft2
The total wall space is therefore: 594 – 21 – 20 = 553 ft2
Compare your answer with the correct one above
A room has dimensions of 23ft by 17ft by 10ft. The last dimension is the height of the room. It has one door that is 2.5ft by 8ft and one window, 3ft by 6ft. There is no trim to the floor, wall, doors, or windows. If one can of paint covers 57 ft2 of surface area. How many cans of paint must be bought to paint the walls of the room.
A room has dimensions of 23ft by 17ft by 10ft. The last dimension is the height of the room. It has one door that is 2.5ft by 8ft and one window, 3ft by 6ft. There is no trim to the floor, wall, doors, or windows. If one can of paint covers 57 ft2 of surface area. How many cans of paint must be bought to paint the walls of the room.
If broken down into parts, this is an easy problem. It is first necessary to isolate the dimensions of the walls. If the room is 10ft high, we know 23 x 17 designates the area of the floor and ceiling. Based on this, we know that the room has the following dimensions for the walls: 23 x 10 and 17 x 10. Since there are two of each, we can calculate the total area of walls - ignoring doors and windows - by doubling the sum of these two areas:
2 * (23 * 10 + 17 * 10) = 2 * (230 + 170) = 2 * 400 = 800 ft2
Now, we merely need to calculate the area "taken out" of the walls:
For the door: 2.5 * 8 = 20 ft2
For the windows: 3 * 6 = 18 ft2
The total wall space is therefore: 800 – 20 – 18 = 762 ft2
Now, if one can of paint covers 57 ft2, we calculate the number of cans necessary by dividing the total exposed area by 57: 762/57 = (approx.) 13.37.
Since we cannot buy partial cans, we must purchase 14 cans.
If broken down into parts, this is an easy problem. It is first necessary to isolate the dimensions of the walls. If the room is 10ft high, we know 23 x 17 designates the area of the floor and ceiling. Based on this, we know that the room has the following dimensions for the walls: 23 x 10 and 17 x 10. Since there are two of each, we can calculate the total area of walls - ignoring doors and windows - by doubling the sum of these two areas:
2 * (23 * 10 + 17 * 10) = 2 * (230 + 170) = 2 * 400 = 800 ft2
Now, we merely need to calculate the area "taken out" of the walls:
For the door: 2.5 * 8 = 20 ft2
For the windows: 3 * 6 = 18 ft2
The total wall space is therefore: 800 – 20 – 18 = 762 ft2
Now, if one can of paint covers 57 ft2, we calculate the number of cans necessary by dividing the total exposed area by 57: 762/57 = (approx.) 13.37.
Since we cannot buy partial cans, we must purchase 14 cans.
Compare your answer with the correct one above
A certain cube has a side length of 25 m. How many square tiles, each with an area of 5 m2, are needed to fully cover the surface of the cube?
A certain cube has a side length of 25 m. How many square tiles, each with an area of 5 m2, are needed to fully cover the surface of the cube?
A cube with a side length of 25m has a surface area of:
25m * 25m * 6 = 3,750 m2
(The surface area of a cube is equal to the area of one face of the cube multiplied by 6 sides. In other words, if the side of a cube is s, then the surface area of the cube is 6_s_2.)
Each square tile has an area of 5 m2.
Therefore, the total number of square tiles needed to fully cover the surface of the cube is:
3,750m2/5m2 = 750
Note: the volume of a cube with side length s is equal to _s_3. Therefore, if asked how many mini-cubes with side length n are needed to fill the original cube, the answer would be:
s3/n3
A cube with a side length of 25m has a surface area of:
25m * 25m * 6 = 3,750 m2
(The surface area of a cube is equal to the area of one face of the cube multiplied by 6 sides. In other words, if the side of a cube is s, then the surface area of the cube is 6_s_2.)
Each square tile has an area of 5 m2.
Therefore, the total number of square tiles needed to fully cover the surface of the cube is:
3,750m2/5m2 = 750
Note: the volume of a cube with side length s is equal to _s_3. Therefore, if asked how many mini-cubes with side length n are needed to fill the original cube, the answer would be:
s3/n3
Compare your answer with the correct one above
A company wants to build a cubical room around a cone so that the cone's height and diameter are 3 inch less than the dimensions of the cube. If the volume of the cone is 486π ft3, what is the surface area of the cube?
A company wants to build a cubical room around a cone so that the cone's height and diameter are 3 inch less than the dimensions of the cube. If the volume of the cone is 486π ft3, what is the surface area of the cube?
To begin, we need to solve for the dimensions of the cone.
The basic form for the volume of a cone is: V = (1/3)πr_2_h
Using our data, we know that h = 2r because the height of the cone matches its diameter (based on the prompt).
486_π_ = (1/3)πr_2 * 2_r = (2/3)_πr_3
Multiply both sides by (3/2_π_): 729 = _r_3
Take the cube root of both sides: r = 9
Note that this is in feet. The answers are in square inches. Therefore, convert your units to inches: 9 * 12 = 108, then add 3 inches to this: 108 + 3 = 111 inches.
The surface area of the cube is defined by: A = 6 * _s_2, or for our data, A = 6 * 1112 = 73,926 in2
To begin, we need to solve for the dimensions of the cone.
The basic form for the volume of a cone is: V = (1/3)πr_2_h
Using our data, we know that h = 2r because the height of the cone matches its diameter (based on the prompt).
486_π_ = (1/3)πr_2 * 2_r = (2/3)_πr_3
Multiply both sides by (3/2_π_): 729 = _r_3
Take the cube root of both sides: r = 9
Note that this is in feet. The answers are in square inches. Therefore, convert your units to inches: 9 * 12 = 108, then add 3 inches to this: 108 + 3 = 111 inches.
The surface area of the cube is defined by: A = 6 * _s_2, or for our data, A = 6 * 1112 = 73,926 in2
Compare your answer with the correct one above
Angie is painting a 2 foot cube for a play she is in. She needs  of paint for every square foot she paints. How much paint does she need?
of paint for every square foot she paints. How much paint does she need?
Angie is painting a 2 foot cube for a play she is in. She needs 
First we must calculate the surface area of the cube. We know that there are six surfaces and each surface has the same area:

Now we will determine the amount of paint needed

First we must calculate the surface area of the cube. We know that there are six surfaces and each surface has the same area:
Now we will determine the amount of paint needed
Compare your answer with the correct one above
According to regulations, the maximum radius of a (spherical) bowling ball is 7.11 centimeters. What does that make the maximum surface area, to the nearest square centimeter?
(Note: disregard the holes)
According to regulations, the maximum radius of a (spherical) bowling ball is 7.11 centimeters. What does that make the maximum surface area, to the nearest square centimeter?
(Note: disregard the holes)
Set  and use the formula for the surface area of a sphere:
and use the formula for the surface area of a sphere:

Set 
Compare your answer with the correct one above
Steve's bedroom measures 20' by 18' by 8' high. He wants to paint the ceiling and all four walls using a paint that gets 360 square feet of coverage per gallon. A one-gallon can of the paint Steve wants costs $36.00; a one-quart can costs $13.00. What is the least amount of money that Steve can expect to spend on paint in order to paint his room?
Steve's bedroom measures 20' by 18' by 8' high. He wants to paint the ceiling and all four walls using a paint that gets 360 square feet of coverage per gallon. A one-gallon can of the paint Steve wants costs $36.00; a one-quart can costs $13.00. What is the least amount of money that Steve can expect to spend on paint in order to paint his room?
Two of the walls have area  ; two have area
; two have area  ; the ceiling has area
; the ceiling has area  .
.
Therefore, the total area Steve wants to cover is

Divide 968 by 360 to get the number of gallons Steve needs to paint his bedroom:

Since  , Steve needs to purchase either two gallon cans and three quart cans, or three gallon cans.
, Steve needs to purchase either two gallon cans and three quart cans, or three gallon cans.
The first option will cost him  ; the second option will cost him
; the second option will cost him  . The latter is the more economical option.
. The latter is the more economical option.
Two of the walls have area 


Therefore, the total area Steve wants to cover is
Divide 968 by 360 to get the number of gallons Steve needs to paint his bedroom:
Since 
The first option will cost him 

Compare your answer with the correct one above

Give the surface area of the above box in square centimeters.

Give the surface area of the above box in square centimeters.
100 centimeters make one meter, so convert each of the dimensions of the box by multiplying by 100.
 centimeters
centimeters
 centimeters
centimeters
Use the surface area formula, substituting  :
:


 square centimeters
square centimeters
100 centimeters make one meter, so convert each of the dimensions of the box by multiplying by 100.


Use the surface area formula, substituting 

Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
Refer to the above diagram, which shows a square. Give the ratio of the area of the yellow region to that of the white region.

Note: Figure NOT drawn to scale.
Refer to the above diagram, which shows a square. Give the ratio of the area of the yellow region to that of the white region.
The area of the entire square is the square of the length of a side, or
 .
.
The area of the right triangle is half the product of its legs, or
 .
.
The area of the yellow region is therefore the difference of the two, or
 .
.
The ratio of the area of the yellow region to that of the white region is
 ; that is, 55 to 9.
; that is, 55 to 9.
The area of the entire square is the square of the length of a side, or

The area of the right triangle is half the product of its legs, or

The area of the yellow region is therefore the difference of the two, or

The ratio of the area of the yellow region to that of the white region is

Compare your answer with the correct one above

The above depicts a rectangular swimming pool for an apartment. The pool is five feet deep everywhere.
An apartment manager wants to paint the four sides and the bottom of the swimming pool. One one-gallon can of the paint he wants to use covers  square feet. How many cans of the paint will the manager need to buy?
square feet. How many cans of the paint will the manager need to buy?

The above depicts a rectangular swimming pool for an apartment. The pool is five feet deep everywhere.
An apartment manager wants to paint the four sides and the bottom of the swimming pool. One one-gallon can of the paint he wants to use covers 
The bottom of the swimming pool has area
 square feet.
square feet.
There are two sides whose area is
 square feet,
square feet,
and two sides whose area is
 square feet.
square feet.
Add the areas:
 square feet.
square feet.
One one-gallon can of paint covers 350 square feet, so divide:

Seven full gallons and part of another are required, so eight is the correct answer.
The bottom of the swimming pool has area

There are two sides whose area is

and two sides whose area is

Add the areas:

One one-gallon can of paint covers 350 square feet, so divide:
Seven full gallons and part of another are required, so eight is the correct answer.
Compare your answer with the correct one above

The surface area of the above cylinder is 80% of what number?

The surface area of the above cylinder is 80% of what number?
The surface area of the cylinder can be calculated by setting  and
and  in the formula
in the formula




This is 80% of the number

The surface area of the cylinder can be calculated by setting 

This is 80% of the number
Compare your answer with the correct one above
What is the surface area of a cube with a side edge of 7?
What is the surface area of a cube with a side edge of 7?
First you must find the area of one side of the cube which is side squared.
 .
.
Then you multiply that area by six since that is how many sides a cube has.
Your answer is  .
.
First you must find the area of one side of the cube which is side squared.

Then you multiply that area by six since that is how many sides a cube has.
Your answer is 
Compare your answer with the correct one above
A rectangular prism has a volume of 70 m3. If the length, width, and height of the prism are integers measured in meters, which of the following is NOT a possible measure of the surface area of the prism measured in square meters?
A rectangular prism has a volume of 70 m3. If the length, width, and height of the prism are integers measured in meters, which of the following is NOT a possible measure of the surface area of the prism measured in square meters?
Since the volume is the product of length, width, and height, and each of these three dimensions are integers, it is important to know the factors of the volume. 70 = (2)(5)(7). This implies that each of these factors (and only these factors with the exception of 1) will show up in the three dimensions exactly once. This creates precisely the following five possibilities:
2, 5, 7
SA = 2((2)(5)+(2)(7)+(5)(7)) = 118
1, 7, 10
SA = 2((1)(7)+(1)(10)+(7)(10)) = 174
1, 5, 14
SA = 2((1)(5)+(1)(14)+(5)(14)) = 178
1, 2, 35
SA = 2((1)(2)+(1)(35)+(2)(35)) = 214
1, 1, 70
SA = 2((1)(1)+(1)(70)+(1)(70)) = 282
Since the volume is the product of length, width, and height, and each of these three dimensions are integers, it is important to know the factors of the volume. 70 = (2)(5)(7). This implies that each of these factors (and only these factors with the exception of 1) will show up in the three dimensions exactly once. This creates precisely the following five possibilities:
2, 5, 7
SA = 2((2)(5)+(2)(7)+(5)(7)) = 118
1, 7, 10
SA = 2((1)(7)+(1)(10)+(7)(10)) = 174
1, 5, 14
SA = 2((1)(5)+(1)(14)+(5)(14)) = 178
1, 2, 35
SA = 2((1)(2)+(1)(35)+(2)(35)) = 214
1, 1, 70
SA = 2((1)(1)+(1)(70)+(1)(70)) = 282
Compare your answer with the correct one above
A cube has a surface area of 10m2. If a cube's sides all double in length, what is the new surface area?
A cube has a surface area of 10m2. If a cube's sides all double in length, what is the new surface area?
The equation for surface area of the original cube is 6s2. If the sides all double in length the new equation is 6(2s)2 or 6 * 4s2. This makes the new surface area 4x that of the old. 4x10 = 40m2
The equation for surface area of the original cube is 6s2. If the sides all double in length the new equation is 6(2s)2 or 6 * 4s2. This makes the new surface area 4x that of the old. 4x10 = 40m2
Compare your answer with the correct one above
The three sides of a rectangular box all have integer unit lengths. If each of the side lengths is greater than one unit, and if the volume of the box is 182 cubic units, what is the surface area of the box in square units?
The three sides of a rectangular box all have integer unit lengths. If each of the side lengths is greater than one unit, and if the volume of the box is 182 cubic units, what is the surface area of the box in square units?
Let's call the side lengths of the box l, w, and h. We are told that l, w, and h must all be integer lengths greater than one. We are also told that the volume of the box is 182 cubic units.
Since the volume of a rectangular box is the product of its side lengths, this means that lwh must equal 182.
(l)(w)(h) = 182.
In order to determine possible values of l, w, and h, it would help us to figure out the factors of 182. We want to express 182 as a product of three integers each greater than 1.
Let's factor 182. Because 182 is even, it is divisible by 2.
182 = 2(91).
91 is equal to the product of 7 and 13.
Thus, 182 = 2(7)(13).
This means that the lengths of the box must be 2, 7, and 13 units.
In order to find the surface area, we can use the following formula:
surface area = 2lw + 2lh + 2hw.
surface area = 2(2)(7) + 2(2)(13) + 2(7)(13)
= 28 + 52 + 182
= 262 square units.
The answer is 262.
Let's call the side lengths of the box l, w, and h. We are told that l, w, and h must all be integer lengths greater than one. We are also told that the volume of the box is 182 cubic units.
Since the volume of a rectangular box is the product of its side lengths, this means that lwh must equal 182.
(l)(w)(h) = 182.
In order to determine possible values of l, w, and h, it would help us to figure out the factors of 182. We want to express 182 as a product of three integers each greater than 1.
Let's factor 182. Because 182 is even, it is divisible by 2.
182 = 2(91).
91 is equal to the product of 7 and 13.
Thus, 182 = 2(7)(13).
This means that the lengths of the box must be 2, 7, and 13 units.
In order to find the surface area, we can use the following formula:
surface area = 2lw + 2lh + 2hw.
surface area = 2(2)(7) + 2(2)(13) + 2(7)(13)
= 28 + 52 + 182
= 262 square units.
The answer is 262.
Compare your answer with the correct one above
A solid sphere is cut in half to form two solid hemispheres. What is the ratio of the surface area of one of the hemispheres to the surface area of the entire sphere before it was cut?
A solid sphere is cut in half to form two solid hemispheres. What is the ratio of the surface area of one of the hemispheres to the surface area of the entire sphere before it was cut?
The surface area of the sphere before it was cut is equal to the following:
surface area of solid sphere = 4_πr_2, where r is the length of the radius.
Each hemisphere will have the following shape:
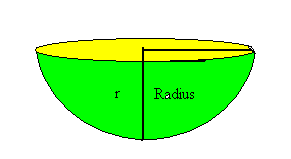
In order to determine the surface area of the hemisphere, we must find the surface area of the flat region and the curved region. The flat region will have a surface area equal to the area of a circle with radius r.
area of flat part of hemisphere = _πr_2
The surface area of the curved portion of the hemisphere will equal one-half of the surface area of the uncut sphere, which we established to be 4_πr_2.
area of curved part of hemisphere = (1/2)4_πr_2 = 2_πr_2
The total surface area of the hemisphere will be equal to the sum of the surface areas of the flat part and curved part of the hemisphere.
total surface area of hemisphere = _πr_2 + 2_πr_2 = 3_πr_2
Finally, we must find the ratio of the surface area of the hemisphere to the surface area of the uncut sphere.
ratio = (3_πr_2)/(4_πr_2) = 3/4
The answer is 3/4.
The surface area of the sphere before it was cut is equal to the following:
surface area of solid sphere = 4_πr_2, where r is the length of the radius.
Each hemisphere will have the following shape:
In order to determine the surface area of the hemisphere, we must find the surface area of the flat region and the curved region. The flat region will have a surface area equal to the area of a circle with radius r.
area of flat part of hemisphere = _πr_2
The surface area of the curved portion of the hemisphere will equal one-half of the surface area of the uncut sphere, which we established to be 4_πr_2.
area of curved part of hemisphere = (1/2)4_πr_2 = 2_πr_2
The total surface area of the hemisphere will be equal to the sum of the surface areas of the flat part and curved part of the hemisphere.
total surface area of hemisphere = _πr_2 + 2_πr_2 = 3_πr_2
Finally, we must find the ratio of the surface area of the hemisphere to the surface area of the uncut sphere.
ratio = (3_πr_2)/(4_πr_2) = 3/4
The answer is 3/4.
Compare your answer with the correct one above