Numbers and Operations on Numbers - HiSet: High School Equivalency Test: Math

Card 0 of 20

Question

Simplify the following expression using scientific notation.

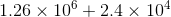
$(1.26\times10^6)+(2.4\times10^4)$

Answer

You can solve this problem in several ways. One way is to convert each number out of scientific notation and write it out fully, then find the sum of the two values and convert the answer back into scientific notation.

$1.26\times10^6+2.4\times10^4 ewline = 1,260,000+24,000 ewline = 1,284,000 ewline = 1.284\times10^6$

Another, potentially faster, way to solve this problem is to convert one answer into the same scientific-notational terms as the other and then sum them.

$1.26\times10^6+2.4\times10^4$

$2.4\times10^{4}=0.024\times10^{6}$

$1.26\times10^6+0.024\times10^6=(1.26+0.024)\times10^6=1.284\times10^6$

Compare your answer with the correct one above

Question

Simplify:

$\sqrt{120}$

Answer

To simplify a radical expression, first find the prime factorization of the radicand, which is 120 here.

$120 = 2 \times 2 \times 2 \times 3 \times 5$

Pair up like factors, then apply the Product of Radicals Property:

$\sqrt{120} =\sqrt{ 2 \times 2 \times 2 \times 3 \times 5} =\sqrt{ 2 \times 2 } \times \sqrt{ 2 \times 3 \times 5} = 2 \sqrt{30}$ ,

the simplest form of the radical.

Compare your answer with the correct one above

Question

Simplify:

$\sqrt{40}$

Answer

To simplify a radical expression, first find the prime factorization of the radicand, which is 40 here.

$40 = 2 \times 2 \times 2 \times 5$

Pair up like factors, then apply the Product of Radicals Property:

$\sqrt{40 }= \sqrt{2 \times 2 \times 2 \times 5} = \sqrt{2 \times 2 } \times \sqrt{ 2 \times 5} = 2 \sqrt{10}$ ,

the simplest form of the radical.

Compare your answer with the correct one above

Question

Simplify:

$\sqrt{32}$

Answer

To simplify a radical expression, first find the prime factorization of the radicand, which is 32 here.

$32 = 2 \times 2 \times 2 \times 2 \times 2$

Pair up like factors, then apply the Product of Radicals Property:

$\sqrt{32} = \sqrt{2 \times 2} \times\sqrt{ 2 \times 2} \times \sqrt{2 }= 2 \times 2 \times \sqrt{2 } = 4 \sqrt{2 }$ ,

the simplest form of the radical.

Compare your answer with the correct one above

Question

Simplify:

$\sqrt{66}$

Answer

To simplify a radical expression, first find the prime factorization of the radicand, which is 66 here.

$66 = 2 \times 3 \times 11$

$\sqrt{66} =\sqrt{ 2 \times 3 \times 11}$

There are no repeated prime factors, so the expression is already in simplified form.

Compare your answer with the correct one above

Question

Simplify the difference:

$\sqrt{70} - \sqrt{30}$

Answer

To simplify a radical expression, first, find the prime factorization of the radicand. First, we will attempt simplify $\sqrt{70}$ as follows:

$70 = 2 \times 5 \times 7$

Since no prime factor appears twice, the expression cannot be simplified further. The same holds for $\sqrt{30}$ , since $30 = 2 \times 3 \times 5$ .

It follows that the expression $\sqrt{70} - \sqrt{30}$ is already in simplest form.

Compare your answer with the correct one above

Question

Simplify the difference:

$\sqrt{176} - \sqrt{11}$

Answer

To simplify a radical expression, first find the prime factorization of the radicand. First, we will simplify $\sqrt{176}$ as follows:

$176 = 2 \times 2 \times 2 \times 2 \times 11$

By the Product of Radicals Property,

$\sqrt{176 }$

$= \sqrt{ 2 \times 2 \times 2 \times 2 \times 11}$

$= \sqrt{2 \times 2} \times \sqrt{2 \times 2} \times \sqrt{11 }$

$=2 \times 2 \times \sqrt{11 }$

$= 4 \sqrt{11}$

11 is a prime number, so $\sqrt{11}$ cannot be simplified. We can replace it with $1\sqrt{11}$ .

Through substitution, and the distribution property:

$\sqrt{176} - \sqrt{11}$

$= 4 \sqrt{11} -1 \sqrt{11}$

$=( 4 -1 )\sqrt{11}$

$=3\sqrt{11}$

Compare your answer with the correct one above

Question

Simplify the sum:

$\sqrt{99}+ \sqrt{44}+ \sqrt{11}$

Answer

To simplify a radical expression, first find the prime factorization of the radicand. First, we will simplify $\sqrt{99}$ as follows:

$99 = 3 \times 3 \times 11$

Pair up like factors, then apply the Product of Radicals Property.

$\sqrt{99} =\sqrt{ 3 \times 3 \times 11} = \sqrt{ 3 \times 3} \times \sqrt{ 11} = 3\sqrt{ 11}$

By similar reasoning,

$44 = 2 \times 2 \times 11$

$\sqrt{44} =\sqrt{ 2 \times 2 \times 11} = \sqrt{ 2 \times 2} \times \sqrt{ 11} = 2\sqrt{ 11}$

11 is a prime number, so $\sqrt{11}$ cannot be simplified. We can replace it with $1\sqrt{11}$ .

Through substitution, and the distribution property:

$\sqrt{99}+ \sqrt{44}+ \sqrt{11}$

$= 3\sqrt{ 11} + 2\sqrt{ 11} + 1 \sqrt{ 11}$

$= (3 + 2 + 1 )\sqrt{ 11}$

$= 6\sqrt{ 11}$

Compare your answer with the correct one above

Question

Simplify the sum:

$\sqrt{11} + \sqrt{22}+ \sqrt{33}$

Answer

To simplify a radical expression, first find the prime factorization of the radicand. First, we will attempt simplify $\sqrt{33}$ as follows:

$33 = 3 \times 11$

Since no prime factor appears twice, the expression cannot be simplified further. The same holds for $\sqrt{22}$ , since $22 = 2 \times 11$ ; the same also holds for $\sqrt{11}$ , since 11 is prime.

It follows that the expression $\sqrt{11} + \sqrt{22}+ \sqrt{33}$ is already in simplest form.

Compare your answer with the correct one above

Question

Simplify the expression:

$\frac{10}{\sqrt{15}}$

Answer

An expression with a radical expression in the denominator is not simplified, so to simplify, it is necessary to rationalize the denominator. This is accomplished by multiplying both numerator and denominator by the given square root, $\sqrt{15}$ , as follows:

$\frac{10}{\sqrt{15}} = \frac{10 \times \sqrt{15}}{\sqrt{15} \times \sqrt{15}} = \frac{10 \sqrt{15}}{15}$

The expression can be simplified further by dividing the numbers outside the radical by greatest common factor 5:

$\frac{10 \sqrt{15}}{15} = \frac{(10 \div 5) \sqrt{15}}{15 \div 5} = \frac{2 \sqrt{15}}{3}$

This is the correct response.

Compare your answer with the correct one above

Question

Simplify the expression

$\frac{6}{\sqrt{12}}$

Answer

An expression with a radical expression in the denominator is not simplified, so to simplify, it is necessary to rationalize the denominator. This is accomplished by multiplying both numerator and denominator by the given square root, $\sqrt{12}$ , as follows:

$\frac{6}{\sqrt{12}} = \frac{6 \times \sqrt{12}}{\sqrt{12} \times \sqrt{12}} = \frac{6 \times \sqrt{12}}{12}$

$\sqrt{12}$ can be simplified by taking the prime factorization of 12, and taking advantage of the Product of Radicals Property.

$12 = 2\times 2 \times 3$ , so

$\sqrt{12} = \sqrt{2 \times 2 \times 3 } = \sqrt{2 \times 2 } \times \sqrt{ 3 } = 2\sqrt{ 3 }$

Returning to the original expression and substituting:

$\frac{6 \times \sqrt{12}}{12} = \frac{6 \times 2 \sqrt{3}}{12} = \frac{12 \sqrt{3}}{12} =\sqrt{3}$ ,

the correct response.

Compare your answer with the correct one above

Question

Consider the expression $\frac{2\sqrt{6} }{ 3 \sqrt{5}}$ .

To simplify this expression, it is necessary to first multiply the numerator and the denominator by:

Answer

When simplifying an fraction with a denominator which is the product of an integer and a square root expression, it is necessary to first rationalize the denominator. This is accomplished by multiplying both halves of the fraction by the square root expression. The correct response is therefore $\sqrt{5}$ .

Compare your answer with the correct one above

Question

Consider the expression $\frac{1+ \sqrt{2}}{3- \sqrt{2}}$ .

To simplify this expression, it is necessary to first multiply the numerator and the denominator by:

Answer

When simplifying a fraction with a denominator which is the sum or difference of an integer and a square root, it is necessary to first rationalize the denominator. This is accomplished by multiplying both halves of the fraction by the conjugate of the denominator—the result of changing the plus symbol to a minus symbol (or vice versa); therefore, both halves of the given expression must be multiplied by the conjugate of $3 - \sqrt{2}$ , which is $3 + \sqrt{2}$ .

$3 + \sqrt{2}$ is therefore the correct choice.

Compare your answer with the correct one above

Question

Multiply: $\left (2 + \sqrt{2x} \right )\left (2 - \sqrt{2x} \right )$

Answer

The two expressions comprise the sum and the difference of the same two expressions, and can be multiplied using the difference of squares formula:

$\left (2 + \sqrt{2x} \right )\left (2 - \sqrt{2x} \right )$

$= 2^{2} - (\sqrt{2x} )^{2}$

The square of the square root of an expression is the expression itself, so:

Compare your answer with the correct one above

Question

Multiply: $(6 + \sqrt{21} )(6 - \sqrt{21} )$

Answer

The two expressions comprise the sum and the difference of the same two expressions, and can be multiplied using the difference of squares formula:

$(6 + \sqrt{21} )(6 - \sqrt{21} )$

$= 6^{2} -( \sqrt{21} )^{2}$

The square of the square root of an expression is the expression itself, so:

Compare your answer with the correct one above

Question

Multiply: $(7+2 \sqrt{7})(7-2 \sqrt{7})$

Answer

The two expressions comprise the sum and the difference of the same two expressions, and can be multiplied using the difference of squares formula:

$(7+2 \sqrt{7})(7-2 \sqrt{7})$

$= 7^{2} -(2 \sqrt{7})^{2}$

The second expression can be rewritten by the Power of a Product Property:

$= 7^{2} -2^{2}( \sqrt{7})^{2}$

The square of the square root of an expression is the expression itself:

By order of operations, multiply, then subtract:

Compare your answer with the correct one above

Question

Multiply: $\left ( \sqrt{7x}-\sqrt{3x} \right )\left ( \sqrt{7x}+\sqrt{3x} \right )$ .

Answer

The two expressions comprise the sum and the difference of the same two expressions, and can be multiplied using the difference of squares formula:

$\left ( \sqrt{7x}-\sqrt{3x} \right )\left ( \sqrt{7x}+\sqrt{3x} \right )$

$= ( \sqrt{7x})^{2}-(\sqrt{3x} )^{2 }$

The square of the square root of an expression is the expression itself:

By distribution:

Compare your answer with the correct one above

Question

Multiply, and express the product in scientific notation:

$7,200,000 \times 5,000,000$

Answer

Convert 7,200,000 to scientific notation as follows:

Move the (implied) decimal point until it is immediately after the first nonzero digit (the 7). This required moving the point six units to the left:

$7,200,000. \Rightarrow 7.200000$

It follows that 7,200,000 can be rewritten as $7.2 \times 10^{6}$ .

By similar reasoning, 5,000,000 can be rewritten as $5 \times 10^{6}$ .

Thus,

$7,200,000 \times 5,000,000$

$= (7.2\times 10 ^{6} )\times (5 \times 10^{6} )$

Rearrange and regroup the expressions so that the powers of ten are together:

$= (7.2\times 5) \times (10 ^{6} \times 10^{6} )$

Multiply the numbers in front. Also, multiply the powers of ten by adding exponents:

$= 36 \times 10 ^{6+6}$

$= 36 \times 10 ^{12}$

In order for the number to be in scientific notation, the number in front must be between 1 and 10. An adjustment must be made by moving the implied decimal point in 36 one unit left. It follows that

$36 = 3.6 \times 10^{1}$

Therefore,

$36 \times 10 ^{12} = (3.6 \times 10^{1}) \times 10 ^{12}$

$= 3.6 \times 10^{1+12}$

$= 3.6 \times 10^{13}$ ,

the correct response.

Compare your answer with the correct one above

Question

Multiply:

$5,000,000 \times 120,000,000$

Express the product in scientific notation.

Answer

Scientific notation refers to a number expressed in the form

$\pm a \times 10^{N}$ ,

where $1 \le a < 10$ and is an integer.

Each factor can be rewritten in scientific notation as follows:

$5,000,000 = 5 \times 1,000,000 = 5 \times 10^{6}$

$120,000,000 = 1.2 \times 100,000,000 = 1.2 \times 10^{8}$

Now, substitute:

$5,000,000 \times 120,000,000$

$= 5 \times 10^{6} \times 1.2 \times 10^{8}$

$=( 5\times 1.2) \times (10^{6} \times 10^{8})$

$= 6 \times 10^{6} \times 10^{8}$

Apply the Product of Powers Property:

$= 6 \times 10^{6+8}$

$= 6 \times 10^{14}$

This is in scientific notation and is the correct choice.

Compare your answer with the correct one above

Question

Multiply, adjusting for significant digits.

$0.00421 \times 0.00332$

Answer

First, determine the number of significant digits in each factor. Both factors have leading zeroes, which must be discounted. Therefore, in each factor, the number of significant digits can be found by counting from the first nonzero digit to the final digit. 0.00421 and 0.00332 each have three significant digits.

Now, multiply the numbers outright. The product, ignoring any trailing zeroes, is

$0.00421 \times 0.00332 = 0.0000139772$

The product must be rounded to the appropriate number of significant digits. This number must be the lesser of the numbers of significant digits that appears in the factors, which is three. Count from the first nonzero digit:

$0.0000\textbf{139{\color{Red} 7}}72$

Rounded, this is 0.0000140, the correct choice. (Note that this trailing zero must be kept in order to have three significant digits.)

Compare your answer with the correct one above

Tap the card to reveal the answer